Семимартингалы
6.1. Определение. Будем говорить, что последовательность 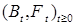 имеет ограниченную вариацию, если Р - п. н. имеет ограниченную вариацию, если Р - п. н. 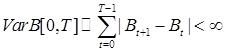 . .
Определение. Последовательность 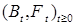 с ограниченной вариацией назовем случайной последовательностью с интегрируемой вариацией, если с ограниченной вариацией назовем случайной последовательностью с интегрируемой вариацией, если  . .
Из определения следует утверждение.
Теорема 22. Пусть 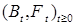 - последовательность с ограниченной вариацией. Тогда существуют две возрастающие последовательности - последовательность с ограниченной вариацией. Тогда существуют две возрастающие последовательности  , такие, что Р - п. н. для любого , такие, что Р - п. н. для любого 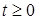  . (Докажите самостоятельно.) . (Докажите самостоятельно.)
6.2. Определение. Последовательность  называется семимартингалом относительно меры Р, если она Р - п. н. для любого называется семимартингалом относительно меры Р, если она Р - п. н. для любого 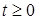 допускает представление допускает представление
 , ,
где  - локальный мартингал относительно меры Р, - локальный мартингал относительно меры Р, 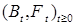 - процесс ограниченной вариации. - процесс ограниченной вариации.
Множество семимартингалов относительно фильтрации  и меры Р обозначим через и меры Р обозначим через  . .
Теорема 23. Последовательность  является относительно меры Р семимартингалом тогда и только тогда, когда она согласована с потоком является относительно меры Р семимартингалом тогда и только тогда, когда она согласована с потоком  . .
Доказательство.Необходимость очевидна.
Достаточность. Поскольку процесс  согласован с потоком согласован с потоком  , то он имеет ограниченную вариацию. Очевидно, что: i) , то он имеет ограниченную вариацию. Очевидно, что: i)  , где , где  , ii) , ii)  Так как для любого Так как для любого  , то существует , то существует 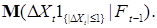 Стало быть Стало быть
 , (14) , (14)
где  такое, что такое, что  - предсказуемо, а - предсказуемо, а  относительно меры Р и потока относительно меры Р и потока  локальный мартингал. Отсюда следует утверждение теоремы так как локальный мартингал. Отсюда следует утверждение теоремы так как  имеет ограниченную вариацию. Доказательство закончено. имеет ограниченную вариацию. Доказательство закончено.
Следствие 24. Пусть  тогда он допускает единственное представление (14). (Докажите самостоятельно.) тогда он допускает единственное представление (14). (Докажите самостоятельно.)
6.3. Определение. Семимартингал  называется специальным, если для любого t ³ 0 он допускает представление называется специальным, если для любого t ³ 0 он допускает представление
 , (15) , (15)
где  - локальный мартингал относительно меры Р, - локальный мартингал относительно меры Р,  - предсказуемая последовательность ограниченной вариации. - предсказуемая последовательность ограниченной вариации.
Теорема 25. Пусть  специальный семимартингал относительно меры Р. Тогда представление (15) единственно. Докажите самостоятельно. специальный семимартингал относительно меры Р. Тогда представление (15) единственно. Докажите самостоятельно.
6.4. Теорема 26 (формула Ито). Пусть  и и  множество ограниченных непрерывно дифференцируемых функций множество ограниченных непрерывно дифференцируемых функций  . Пусть . Пусть  семимартингал относительно меры Р. Тогда Р - п. н. справедливо равенство семимартингал относительно меры Р. Тогда Р - п. н. справедливо равенство
 (16) (16)
где  - скалярное произведение в - скалярное произведение в  . .
Доказательство. Очевидно равенство  Р - п. н. Отсюда следует (16). Доказательство закончено. Р - п. н. Отсюда следует (16). Доказательство закончено.
6.5. Их формулы Ито (16) легко получить представление для произведения семимартингалов.
Теорема 27. Пусть  и и 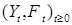 семимартингалы со значениями семимартингалы со значениями  относительно меры P. Тогда P – п.н. справедливо равенство относительно меры P. Тогда P – п.н. справедливо равенство
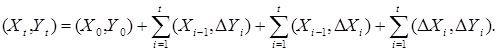
В частности 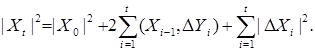
(Докажите самостоятельно).
Определение. Квадратической вариацией семимартингала  , обозначаемого через , обозначаемого через  , назовем случайную последовательность определяемую равенством , назовем случайную последовательность определяемую равенством
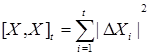
Определение. Взаимной вариацией семимартингалов  и и 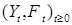 , обозначаемую через , обозначаемую через  назовем случайную последовательность такую, что назовем случайную последовательность такую, что  . .
Дата добавления: 2015-01-18 | Просмотры: 699 | Нарушение авторских прав
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|

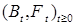 имеет ограниченную вариацию, если Р - п. н.
имеет ограниченную вариацию, если Р - п. н. 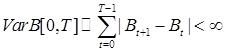 .
. .
. , такие, что Р - п. н. для любого
, такие, что Р - п. н. для любого 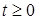
 . (Докажите самостоятельно.)
. (Докажите самостоятельно.) называется семимартингалом относительно меры Р, если она Р - п. н. для любого
называется семимартингалом относительно меры Р, если она Р - п. н. для любого  ,
, - локальный мартингал относительно меры Р,
- локальный мартингал относительно меры Р,  и меры Р обозначим через
и меры Р обозначим через  .
. является относительно меры Р семимартингалом тогда и только тогда, когда она согласована с потоком
является относительно меры Р семимартингалом тогда и только тогда, когда она согласована с потоком  , где
, где  , ii)
, ii)  Так как для любого
Так как для любого  , то существует
, то существует 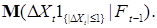 Стало быть
Стало быть , (14)
, (14) такое, что
такое, что  - предсказуемо, а
- предсказуемо, а  относительно меры Р и потока
относительно меры Р и потока  имеет ограниченную вариацию. Доказательство закончено.
имеет ограниченную вариацию. Доказательство закончено. тогда он допускает единственное представление (14). (Докажите самостоятельно.)
тогда он допускает единственное представление (14). (Докажите самостоятельно.) - локальный мартингал относительно меры Р,
- локальный мартингал относительно меры Р,  - предсказуемая последовательность ограниченной вариации.
- предсказуемая последовательность ограниченной вариации. и
и  множество ограниченных непрерывно дифференцируемых функций
множество ограниченных непрерывно дифференцируемых функций  . Пусть
. Пусть  (16)
(16) - скалярное произведение в
- скалярное произведение в  .
. Р - п. н. Отсюда следует (16). Доказательство закончено.
Р - п. н. Отсюда следует (16). Доказательство закончено.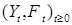 семимартингалы со значениями
семимартингалы со значениями 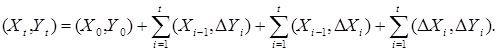
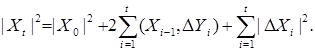
 , назовем случайную последовательность определяемую равенством
, назовем случайную последовательность определяемую равенством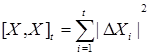
 назовем случайную последовательность такую, что
назовем случайную последовательность такую, что  .
.