АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология

Третья теорема двойственности

Заданным значениям констант задачи линейного программирования соответствуют оптимальный план и оптимум (если они существуют). При изменении констант решение задачи также будет изменяться (т.е. другим исходным данным может соответствовать другое решение). Рассмотрим оптимум задачи, как функцию от свободных членов ограничений Z^*(B) (в самом деле, каждому набору значений свободных членов будет соответствовать одно значение оптимума, если задача разрешима).

Теорема 3 (об оценке). Частные производные Z^*(B) по элементам столбца свободных членов равны оптимальным значениям соответствующих двойственных переменных:

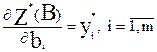
Это означает, что двойственная переменная показывает, на сколько изменится оптимум задачи при изменении свободного члена в соответствующем ограничении на единицу*.

В задаче производственного планирования двойственные переменные показывают, как повлияет на общую выручку изменение запаса ресурса на единицу. Поскольку двойственные переменные позволяют оценить влияние на оптимум каждого ограничения, их называют двойственными оценками, или теневыми ценами.

Например, для задачи, решенной в разделе 3.3, теневые цены сахарного песка, патоки и фруктового пюре равны соответственно у₁^*» 125; у₂^* = 0 и у₃^*» 773. Это означает, что при увеличении запасов сахарного песка на одну тонну оптимальная прибыль фабрики возрастет на 125 руб., при увеличении запасов патоки эта прибыль не изменится, а на каждую тонну увеличения запасов фруктового пюре рост прибыли составит 773 руб.

Если исходные данные задачи изменятся, и будет известно, что запасы сахарного песка составляют, например, 810 т, то для определения оптимальной прибыли нет необходимости решать задачу заново. В самом деле, зная, что запас сахара возрос на 810 – 800 = 10 (т), можно сделать вывод, что прибыль возросла на 125*10 = 1250 (руб.). Т.к. ранее оптимальная прибыль составляла 193067 руб., то можно подсчитать, что при новых запасах сахарного песка она составит 193067 + 1250 = 194317 (руб.).

Однако следует помнить о том, что элементы столбца свободных членов являются коэффициентами целевой функции двойственной задачи. При изменении коэффициентов целевой функции на некотором интервале оптимальный план задачи остается неизменным, но за его пределами происходит переход к другому оптимальному плану, и третья теорема двойственности теряет свой смысл. Это хорошо видно на рисунке 27 (при графическом решении задачи с изменением коэффициентов целевой функции изменяются координаты ее градиента, который при этом как бы «поворачивается»).

Поэтому применение теоремы об оценке необходимо дополнять анализом устойчивости двойственных оценок, т.е. для каждого элемента столбца свободных членов найти интервал его изменения, при котором оптимальные двойственные оценки остаются неизменными.

Применительно к симплексной таблице это означает следующее. Если в исходную симплексную таблицу подставить другие значения свободных членов и подвергнуть их всем тем же линейным преобразованиям, что и первоначальные исходные данные, то последняя симплексная таблица также изменится. При этом изменится только содержимое столбца В (так как при пересчете других столбцов свободные члены не используются). Поэтому коэффициенты критериальной строки (они же оптимальные значения двойственных переменных) останутся прежними, и критерий оптимальности будет выполняться. Однако, может нарушиться критерий допустимости, т.е. в столбце В могут появиться отрицательные числа. Если они не появились, это означает, что свободные члены остались в диапазоне устойчивости двойственных оценок, и теневыми ценами можно пользоваться. В противном случае этого делать нельзя. При проведении анализа устойчивости обычно рассматривают изменение свободных членов по одному, полагая остальные постоянными.

Пример проведения анализа устойчивости будет рассмотрен в разделе 5.6.4. Вопрос о том, изменятся ли теневые цены в задаче о кондитерской фабрике при изменении запасов сахарного песка, патоки и фруктового пюре на 1 т, или на 10 т и т.п., будет решен в разделе 6.6.2.

Задача производственного планирования позволяет также выявить экономический смысл дополнительных переменных двойственной задачи.

Если привести двойственную задачу к канонической форме с помощью дополнительных переменных и затем построить к ней двойственную, то переменные этой новой задачи должны быть не ограничены по знаку (так как соответствуют ограничениям-равенствам). Но поскольку дополнительные переменные входят по одной в каждое ограничение с коэффициентом 1 и все в целевую функцию с коэффициентом 0, им в новой задаче будут соответствовать новые ограничения х₁ ³ 0,... х_j ³ 0,... х_n ³ 0, которые сами по себе определяют знак переменных; т.е. эта задача будет эквивалентна исходной.

Для исходной задачи, записанной в таком виде, тоже выполняются теоремы двойственности. При этом по теореме о равновесии если дополнительная переменная двойственной задачи отлична от нуля, то соответствующее ей ограничение исходной задачи будет выполняться как равенство, т.е. х_j = 0, переменная небазисная. Если изменить свободный член (0) на единицу, получим х_j ³ 1 (при таком условии эта переменная обязательно должна стать базисной, т.к. нулевой она уже быть не может). По теореме об оценке значение двойственной оценки показывает, на сколько изменится оптимум при изменении свободного члена на единицу. Таким образом, дополнительная переменная двойственной задачи показывает, на сколько изменится оптимум при включении небазисной переменной в базис с единичным значением.

В задаче производственного планирования дополнительная переменная двойственной задачи может быть отлична от нуля только для тех видов продукции, которые выпускать вообще не выгодно. Эта переменная показывает, на сколько уменьшится оптимальная прибыль, если обязательно требуется выпустить хотя бы единицу такого вида продукции. Дополнительные переменные двойственной задачи иногда называют сокращенными затратами (сокращенными за счет отказа от выпуска некоторого вида продукции), или редуцированной стоимостью.

Поскольку в задаче, решенной в разделе 3.3, было выгодно выпускать оба вида карамели – и «Снежинку», и «Яблочную», - обе дополнительные переменные равнялись нулю. Предположим, что при других величинах прибыли на тонну карамели выпускать «Яблочную», стало невыгодно, и х₂^*= 0 (фабрика выпускает только карамель «Снежинка»). Тогда переменная у₅^* могла бы быть отличной от нуля. Предположим, что она оказалась равна, например, 3,75. Это означало бы, что если фабрику обяжут выпустить хотя бы 1 тонну карамели «Яблочная», ее оптимальная прибыль при этом уменьшится на 3,75 руб. (см. раздел 6.8).

Обычно решение задачи линейного программирования дополняется анализом чувствительности (постоптимизационным анализом), который включает в себя:

а) нахождение оптимального плана двойственной задачи;

б) анализ устойчивости двойственных оценок;

в) нахождение интервалов изменения коэффициентов целевой функции исходной задачи, при которых ее оптимальный план остается неизменным.

Поскольку двойственность является взаимной, последний этап можно рассматривать, как анализ устойчивости двойственных оценок для двойственной задачи.

Дата добавления: 2015-01-18 | Просмотры: 982 | Нарушение авторских прав