АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология

Траектории винеровского процесса удовлетворяют условию Гёльдера

Прочитайте:
  1. I ЗВЕНО ЭПИДЕМИЧЕСКОГО ПРОЦЕССА: ИСТОЧНИК ИНФЕКЦИИ
  2. I. Определение инфекционного процесса и формы его проявления.
  3. III ЗВЕНО ЭПИДЕМИЧЕСКОГО ПРОЦЕССА: ВОСПРИИМЧИВЫЙ ОРГАНИЗМ
  4. Абсолютная непрерывность вероятностных мер, соответствующих скачкообразным процессам.
  5. Активные метаболиты и их роль в инициации токсического процесса
  6. Б. Стадия опухолевого процесса.
  7. Биологические последствия активации свободно-радикального процесса в клетке
  8. Бредовым идеям присущи ошибочные основания («паралогика», «кривая логика»). Этих нарушений мы касались, рассматривая нарушения ассоциативного процесса мышления.
  9. В зависимости от физических факторов, тяжести и напряженности трудового процесса
  10. В каких случаях можно говорить о проявлениях эпидемического процесса? (2)

,

где С – некоторая константа, а

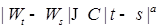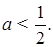
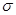1.5. В данном пункте мы покажем, что –алгебра, порожденная винеровским процессом 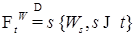, обладает свойством непрерывности слева и справа.

Обозначим .

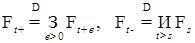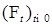Определение. Будем говорить, что фильтрация непрерывна справа (слева), если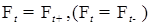

Теорема 6. Пусть на стохастическом базисе 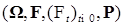задан одномерный винеровский процесс 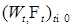. Пусть 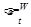- фильтрация пополнена множествами нулевой меры Р. Тогда фильтрация непрерывна справа и слева, т.е. 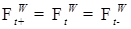для любого 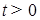. Доказательство. Установим сначала непрерывность слева, т.е. покажем, что 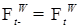. Очевидно, что 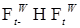. Поэтому нам надо доказать, что 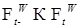. Заметим сначала, что числа в силу непрерывности винеровского процесса, 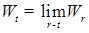, где r - рациональные но тогда , т.е. .

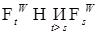Установим теперь непрерывность справа, т.е. 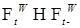. 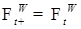Очевидно, что 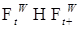. Поэтому надо доказать, что 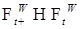. Пусть 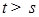. Тогда из определения винеровского процесса следует, что .

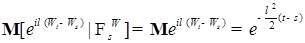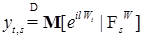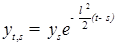Отсюда ясно, что если , то . Следовательно , поэтому P - п. н.

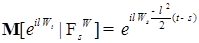(6)

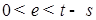Пусть . Тогда из (6) имеем P - п. н.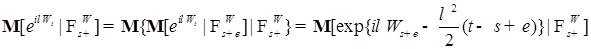

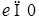Устремим , имеем P - п. н.

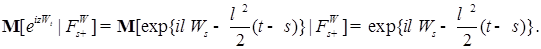(7)

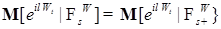Сравнивая (6) и (7), видим, что . Отсюда вытекает, что для любой измеримой ограниченной функции f P - п. н. справедливо равенство

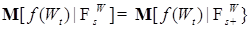. (8)

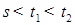Пусть теперь и 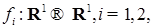- ограниченные измеримые функции. Тогда в силу марковского свойства винеровского процесса и (8) имеем P - п. н.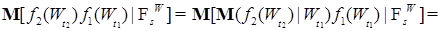

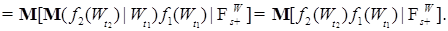
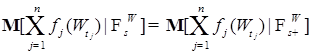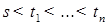Аналогичным образом устанавливается равенство P - п. н. ,

где и 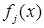- любые измеримые ограниченные функции 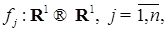.Отсюда следует, что для любой 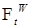-измеримой функции 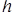P - п. н. имеем 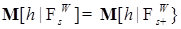. Беря в качестве 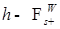измеримую величину, имеем 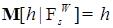P - п. н. Следовательно, 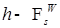- измерима. Значит, 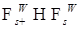. Доказательство закончено.

Дата добавления: 2015-01-18 | Просмотры: 558 | Нарушение авторских прав


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |

При использовании материала ссылка на сайт medlec.org обязательна! (0.003 сек.)