Частные производные и дифференциал функции нескольких переменных
Рассмотрим функцию двух переменных  , определенную в некоторой области , определенную в некоторой области 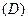 . Возьмем в области . Возьмем в области 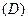 произвольную точку произвольную точку 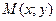 , придадим аргументу х приращение , придадим аргументу х приращение  , а аргумент у оставим без изменения, т.е. перейдем от точки , а аргумент у оставим без изменения, т.е. перейдем от точки 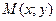 к точке к точке 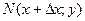 , тоже принадлежащей области , тоже принадлежащей области  .Тогда функция получит частное приращение .Тогда функция получит частное приращение 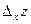 , соответствующее приращению , соответствующее приращению  только одного аргумента х: только одного аргумента х: 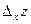 = = 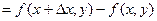 . Составим отношение . Составим отношение 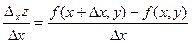 . Если существует конечный предел этого отношения при . Если существует конечный предел этого отношения при 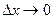 , то он называется частной производной функции , то он называется частной производной функции  по независимой переменной х в точке по независимой переменной х в точке 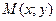 и обозначается и обозначается 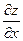 или или 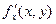 . Иными словами, . Иными словами,
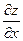 = = 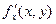 = = 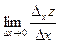 = = 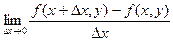 . .
Аналогично определяются частная производная функции  по независимой переменной у в точке по независимой переменной у в точке 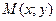 : :
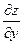 = = 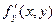 = = 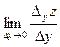 = = 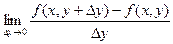
и частные производные функции любого числа переменных. Например, для функции 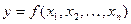
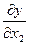 = = 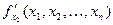 = = 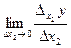 = = 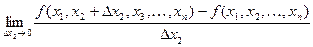 . .
Из определения частной производной следует и правило для нахождения частных производных. Например, чтобы найти частную производную функции  по х в точке по х в точке 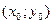 , нужно считать аргумент у постоянным и дифференцировать , нужно считать аргумент у постоянным и дифференцировать 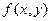 как функцию одной переменной х. Затем в полученное выражение вместо х и у подставить как функцию одной переменной х. Затем в полученное выражение вместо х и у подставить 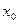 и и 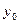 . .
Пример 1. Найдем частные производные 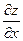 и и 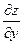 функции функции 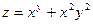 в точке в точке 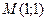 . .
Решение. Имеем
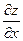 = = 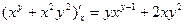 , , 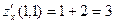 ; ; 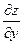 = = 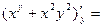 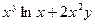 , , 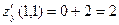 . .
Подсчитаем теперь изменение функции  при переходе от точки при переходе от точки 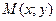 к точке к точке 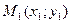 области определения функции. Разность значений функции в точках области определения функции. Разность значений функции в точках 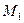 и М называется полным приращением функции и М называется полным приращением функции  при переходе из точки М в точку при переходе из точки М в точку 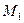 , обозначается , обозначается 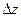 или или 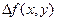 , т.е. , т.е. 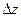 = = 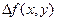 = = 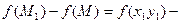 – – 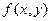 . При переходе из точки М в точку . При переходе из точки М в точку 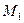 аргументы тоже получают приращения аргументы тоже получают приращения 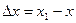 и и 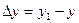 . Тогда . Тогда 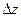 можно записать в виде можно записать в виде 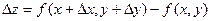 . Геометрически полное приращение функции означает приращение аппликаты z при переходе из точки М в точку . Геометрически полное приращение функции означает приращение аппликаты z при переходе из точки М в точку  . .
При определении дифференциала функции одной переменной важную роль играла форма записи приращения функции 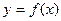 . Если . Если 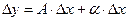 , где , где 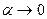 при при 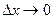 , то функцию , то функцию 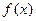 называли дифференцируемой, а первое слагаемое в выражении для называли дифференцируемой, а первое слагаемое в выражении для 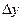 – дифференциалом функции – дифференциалом функции 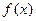 . Аналогичная ситуация имеет место и в случае функции нескольких переменных. . Аналогичная ситуация имеет место и в случае функции нескольких переменных.
Определение 1. Функция  называется дифференцируемой в точке называется дифференцируемой в точке 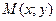 , если ее полное приращение в этой точке можно представить в виде , если ее полное приращение в этой точке можно представить в виде
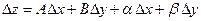 , (19.1) , (19.1)
где А и В не зависят от приращений  и и 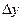 , а , а 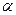 и и 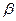 – некоторые функции от – некоторые функции от  и и 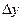 , стремящиеся к нулю при , стремящиеся к нулю при 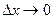 и и 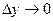 . Выражение . Выражение 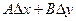 называется полным дифференциалом функции называется полным дифференциалом функции  и обозначается и обозначается 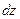 или или 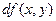 , а его слагаемые , а его слагаемые 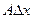 и и 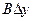 называются частными дифференциалами функции называются частными дифференциалами функции  по х и по у соответственно и обозначаются по х и по у соответственно и обозначаются 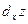 и и 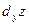 . .
Таким образом, 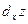 = = 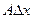 , , 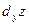 = = 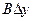 , , 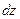 = = 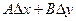 , где А и В не зависят от , где А и В не зависят от  и и 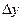 . .
Теорема 1. Если функция  дифференцируема в точке дифференцируема в точке 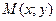 , то она непрерывна в этой точке. , то она непрерывна в этой точке.
Доказательство. В силу дифференцируемости функции в точке 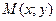 можно записать можно записать 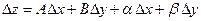 . Отсюда следует, что . Отсюда следует, что 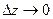 при при 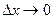 и и 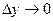 , т.е. , т.е. 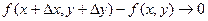 . Следовательно, . Следовательно, 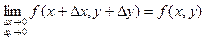 или или 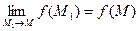 , что и означает непрерывность функции , что и означает непрерывность функции 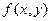 в точке в точке 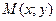 . Теорема доказана. . Теорема доказана.
Теорема 2 (необходимое условие дифференцируемости функции). Если функция  дифференцируема в точке дифференцируема в точке 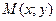 , то она в этой точке имеет частные производные , то она в этой точке имеет частные производные 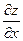 и и 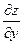 . .
Доказательство. Поскольку функция  дифференцируема, имеем представление дифференцируема, имеем представление 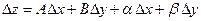 . Пусть . Пусть 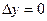 , , 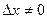 . Тогда . Тогда 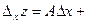 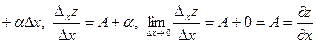 . Аналогично, если . Аналогично, если 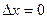 , , 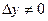 , то , то 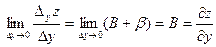 . Так как А и В конечны, то . Так как А и В конечны, то 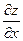 и и 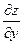 тоже конечны, следовательно, существуют. Теорема доказана. тоже конечны, следовательно, существуют. Теорема доказана.
Поскольку полный дифференциал 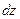 = = 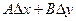 , подставляя , подставляя 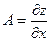 и и 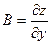 , получим выражение дифференциала через частные производные: , получим выражение дифференциала через частные производные: 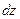 = = 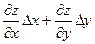 . Отсюда при . Отсюда при 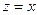 и и 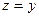 находим находим 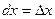 и и 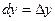 , поэтому , поэтому 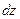 = = 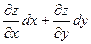 . .
Аналогичное выражение имеет место и для функции любого числа переменных, т.е. если 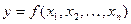 , то , то 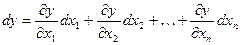 . .
В случае функции одной переменной существования производной было достаточно для дифференцируемости функции. Для функции нескольких переменных ситуация другая: существования частных производных не достаточно для ее дифференцируемости. Имеет место
Теорема 3. Если существуют частные производные функции  , непрерывные в точке , непрерывные в точке 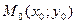 , то в этой точке функция дифференцируема. , то в этой точке функция дифференцируема.
Доказательство. Поскольку, по условию, частные производные непрерывны в точке 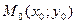 , они существуют в некоторой окрестности этой точки. Рассмотрим приращение данной функции при переходе из точки , они существуют в некоторой окрестности этой точки. Рассмотрим приращение данной функции при переходе из точки 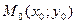 в точку в точку 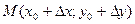 , которая принадлежит указанной окрестности: , которая принадлежит указанной окрестности:
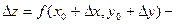 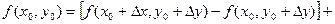 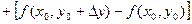 . .
В первой квадратной скобке получилось приращение функции при переходе из точки 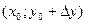 в точку в точку 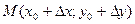 , при этом изменилась только одна переменная х. Поэтому по формуле Лагранжа можно записать: , при этом изменилась только одна переменная х. Поэтому по формуле Лагранжа можно записать:
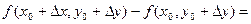 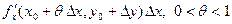 . .
Аналогично, для второй квадратной скобки имеем:
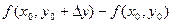 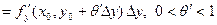 . .
Тогда полное приращение
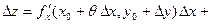 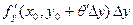 . .
В силу непрерывности частных производных в точке 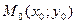 имеем: имеем:
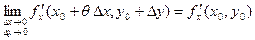 , , 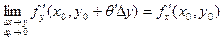 . .
Следовательно, 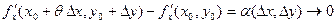 при при  и и 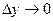 , ,  при при 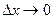 и и 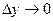 . Тогда . Тогда
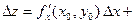 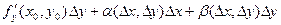 . .
Таким образом, приращение 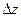 представлено в виде (19.1), поэтому функция представлено в виде (19.1), поэтому функция 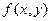 дифференцируема в точке дифференцируема в точке 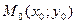 . Теорема доказана. . Теорема доказана.
Выведем теперь формулы для вычисления производных сложной функции нескольких переменных. Сначала рассмотрим случай дифференцируемой функции  , аргументы которой зависят от одной переменной t, т.е. , аргументы которой зависят от одной переменной t, т.е.  , причем функции , причем функции 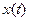 и и 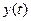 тоже дифференцируемы. Нужно найти производную тоже дифференцируемы. Нужно найти производную 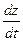 . Пусть аргумент t получает приращение . Пусть аргумент t получает приращение 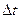 . Тогда х и у получат соответствующие приращения . Тогда х и у получат соответствующие приращения 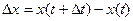 , , 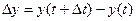 , причем , причем 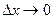 и и 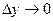 при при 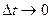 в силу непрерывности дифференцируемой функции. Функция в силу непрерывности дифференцируемой функции. Функция  тоже получит приращение тоже получит приращение 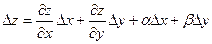 в силу ее дифференцируемости. Отсюда в силу ее дифференцируемости. Отсюда
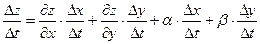 , , 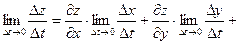 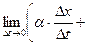 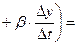 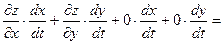 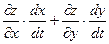 . .
Таким образом,
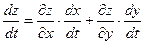 . (19.1) . (19.1)
Заметим, что знак 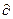 пишется тогда, когда находится частная производная функции по одной из нескольких переменных, знак d – тогда, когда производная находится по основному аргументу, и этот аргумент единственный. пишется тогда, когда находится частная производная функции по одной из нескольких переменных, знак d – тогда, когда производная находится по основному аргументу, и этот аргумент единственный.
Может получиться так, что у функции  переменная у зависит от х, т.е. переменная у зависит от х, т.е. 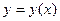 . Тогда основным аргументом является х и формула (19.1) принимает вид . Тогда основным аргументом является х и формула (19.1) принимает вид
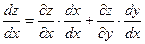 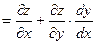 . .
В случае, когда количество аргументов у функции z больше двух, но все они зависят от одного аргумента t, то получается формула, аналогичная формуле (19.1). Например, для функции 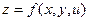 , где , где 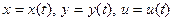 имеем имеем
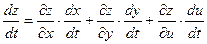 . (19.2) . (19.2)
Теперь рассмотрим случай, когда основных аргументов два, а не один. Пусть 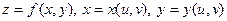 . Здесь уже производные по основным аргументам будут частными производными (их два). Положим . Здесь уже производные по основным аргументам будут частными производными (их два). Положим 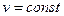 и найдем и найдем 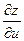 , воспользовавшись формулой (19.1): , воспользовавшись формулой (19.1):
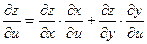 . .
Аналогично,
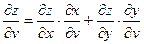 . .
В случае большего числа переменных формулы получаются аналогично.
Для функции 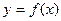 одной переменной известно, что форма дифференциала одной переменной известно, что форма дифференциала 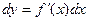 остается неизменной, если заменить независимую переменную х функцией. Имеет ли место это свойство для функции нескольких переменных? Выясним это. остается неизменной, если заменить независимую переменную х функцией. Имеет ли место это свойство для функции нескольких переменных? Выясним это.
Если  , где х и у – независимые переменные, то, как показано выше, , где х и у – независимые переменные, то, как показано выше,
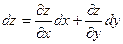 . .
Пусть теперь х и у – функции, 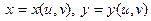 . Поскольку теперь ухе u и v – независимые переменные, имеем . Поскольку теперь ухе u и v – независимые переменные, имеем
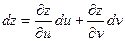 . .
(предполагаем, что для всех функций выполняются достаточные условия дифференцируемости). По правилу дифференцирования сложной функции
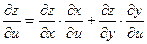 , , 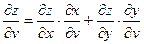 , ,
поэтому
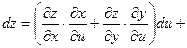 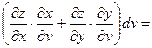 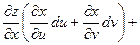 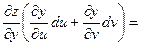 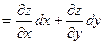 , т.е. формула для вычисления дифференциала сохраняется и в случае, когда х и у – функции. Таким образом, форма дифференциала является инвариантной, т.е. неизменной и для независимых переменных х и у, и для функций х и у. , т.е. формула для вычисления дифференциала сохраняется и в случае, когда х и у – функции. Таким образом, форма дифференциала является инвариантной, т.е. неизменной и для независимых переменных х и у, и для функций х и у.
Рассмотрим теперь частные производные и дифференциалы высших порядков. Пусть  . Для функций большего числа переменных рассуждения аналогичны. . Для функций большего числа переменных рассуждения аналогичны.
Частные производные 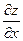 и и 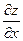 в свою очередь могут оказаться функциями двух переменных. Если от них снова найти частные производные, то они называются частными производными 2-го порядка и обозначаются в свою очередь могут оказаться функциями двух переменных. Если от них снова найти частные производные, то они называются частными производными 2-го порядка и обозначаются 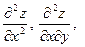 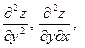 при этом при этом 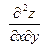 и и 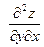 называются смешанными производными. Например, для функции называются смешанными производными. Например, для функции 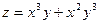 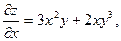 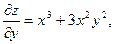 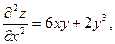 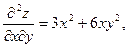 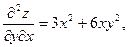 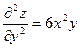 . Аналогично определяются частные производные 3-го, 4-го и т.д. порядка. . Аналогично определяются частные производные 3-го, 4-го и т.д. порядка.
Видим, что в приведенном примере 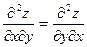 . Всегда ли так будет или это случайное совпадение? Имеет место . Всегда ли так будет или это случайное совпадение? Имеет место
Теорема 4 (о равенстве смешанных производных). Если функция  : 1) определена в открытой области D; 2) в этой области существуют первые производные : 1) определена в открытой области D; 2) в этой области существуют первые производные 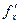 и и 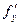 , а также вторые смешанные производные , а также вторые смешанные производные 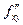 и и 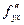 ; 3) производные ; 3) производные 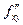 и и 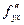 непрерывны в некоторой точке непрерывны в некоторой точке 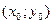 области D, то области D, то
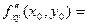 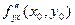 . .
Доказательство. Рассмотрим вспомогательное выражение
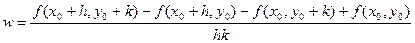 , (19.3) , (19.3)
где h и k отличны от нуля и настолько малы, что в D содержится весь прямоугольник 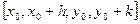 . Пусть . Пусть 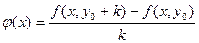 – вспомогательная функция, дифференцируемая на отрезке – вспомогательная функция, дифференцируемая на отрезке 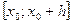 в силу 2-го условия теоремы и, следовательно, непрерывная. Имеем в силу 2-го условия теоремы и, следовательно, непрерывная. Имеем 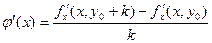 . Выражение (19.3) с помощью . Выражение (19.3) с помощью 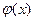 записывается следующим образом: записывается следующим образом:
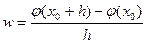 . (19.4) . (19.4)
С помощью формулы Лагранжа последнее равенство запишется в виде
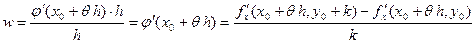 . .
Поскольку 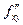 существует, по формуле Лагранжа по у получаем существует, по формуле Лагранжа по у получаем
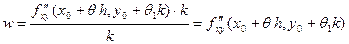 . .
Рассуждая аналогично, с помощью вспомогательной функции
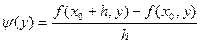
из (19.3) получим 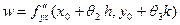 , поэтому , поэтому
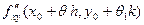 = = 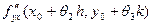 . .
Переходя в последнем равенстве к пределу при 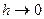 и и 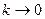 и учитывая, что и учитывая, что 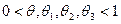 и смешанные производные непрерывны, получим и смешанные производные непрерывны, получим
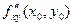 = = 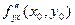 . .
Теорема доказана.
Пусть  – функция двух независимых переменных х и у, дифференцируемая в области D. Тогда в этой области функция имеет полный дифференциал – функция двух независимых переменных х и у, дифференцируемая в области D. Тогда в этой области функция имеет полный дифференциал
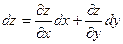 , ,
где 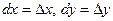 . Зафиксируем . Зафиксируем  и и 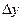 . Тогда дифференциал . Тогда дифференциал 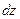 является функцией только переменных х и у, определенной в области D. Полный дифференциал от дифференциала является функцией только переменных х и у, определенной в области D. Полный дифференциал от дифференциала 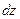 называется дифференциалом 2-го порядка или вторым дифференциалом функции называется дифференциалом 2-го порядка или вторым дифференциалом функции  и обозначается и обозначается 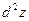 или или 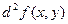 . Таким образом, по определению . Таким образом, по определению 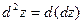 . Учитывая, что . Учитывая, что 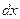 и и 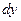 постоянны, находим постоянны, находим
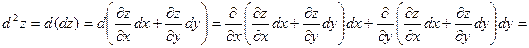 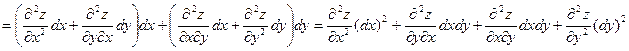 . .
Предполагая частные производные второго порядка непрерывными в области D, получим, что смешанные производные равны и
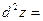 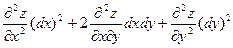 . .
Аналогично, если в области D функция  имеет непрерывные частные производные 3-го порядка, то дифференциал от дифференциала имеет непрерывные частные производные 3-го порядка, то дифференциал от дифференциала 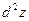 называется ее дифференциалом 3-го порядка или третьим дифференциалом и вычисляется по формуле называется ее дифференциалом 3-го порядка или третьим дифференциалом и вычисляется по формуле
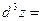 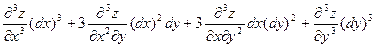 , ,
и т.д.
Символически можно записать
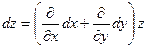 , ,
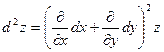 , ,
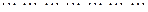
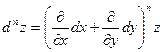 . .
Здесь правую часть нужно понимать так: двучлен в скобках возводится формально в соответствующую степень и результат почленно умножается на z, полученные произведения считаются производными соответствующих порядков.
Пример 2. Для функции 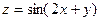 найдем найдем 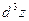 в точке в точке 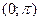 . .
Решение. Найдем частные производные 3-го порядка данной функции, вычислим их в данной точке и подставим в формулу для 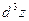 . Имеем . Имеем
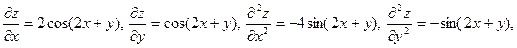
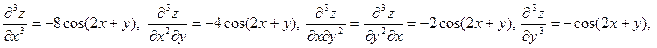
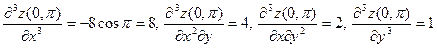
и
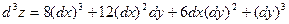 . .
В случае большего числа переменных формулы получаются аналогично. Например, для функции 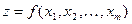
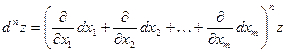 . .
Если переменные х и у не являются независимыми переменными, то (как и в случае функции одной переменной) форма записи дифференциалов высших порядков изменяется, т.е. дифференциалы высших порядков не обладают свойством инвариантности их формы. Например, для функции 
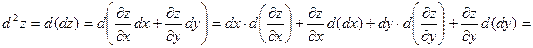
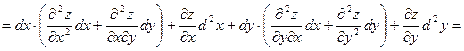 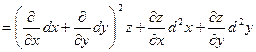 . .
Здесь уже х и у – функции, поэтому 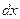 и и 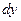 – функции, и – функции, и 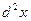 и и 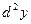 не равны нулю. не равны нулю.
Дата добавления: 2015-01-18 | Просмотры: 1328 | Нарушение авторских прав
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|

 , определенную в некоторой области
, определенную в некоторой области 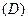 . Возьмем в области
. Возьмем в области 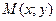 , придадим аргументу х приращение
, придадим аргументу х приращение  , а аргумент у оставим без изменения, т.е. перейдем от точки
, а аргумент у оставим без изменения, т.е. перейдем от точки 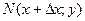 , тоже принадлежащей области
, тоже принадлежащей области 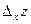 , соответствующее приращению
, соответствующее приращению 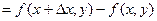 . Составим отношение
. Составим отношение 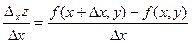 . Если существует конечный предел этого отношения при
. Если существует конечный предел этого отношения при  , то он называется частной производной функции
, то он называется частной производной функции 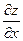 или
или 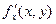 . Иными словами,
. Иными словами,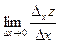 =
= 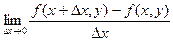 .
.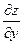 =
= 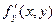 =
= 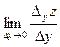 =
= 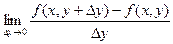
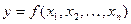
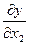 =
= 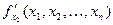 =
= 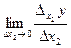 =
= 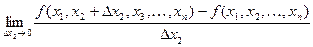 .
.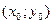 , нужно считать аргумент у постоянным и дифференцировать
, нужно считать аргумент у постоянным и дифференцировать 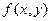 как функцию одной переменной х. Затем в полученное выражение вместо х и у подставить
как функцию одной переменной х. Затем в полученное выражение вместо х и у подставить 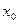 и
и 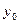 .
.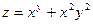 в точке
в точке 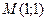 .
.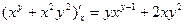 ,
, 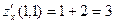 ;
; 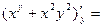
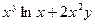 ,
, 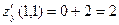 .
. области определения функции. Разность значений функции в точках
области определения функции. Разность значений функции в точках 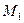 и М называется полным приращением функции
и М называется полным приращением функции 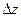 или
или 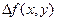 , т.е.
, т.е. 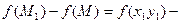 –
– 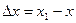 и
и 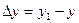 . Тогда
. Тогда 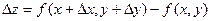 . Геометрически полное приращение функции означает приращение аппликаты z при переходе из точки М в точку
. Геометрически полное приращение функции означает приращение аппликаты z при переходе из точки М в точку 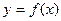 . Если
. Если 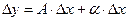 , где
, где 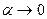 при
при 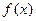 называли дифференцируемой, а первое слагаемое в выражении для
называли дифференцируемой, а первое слагаемое в выражении для 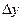 – дифференциалом функции
– дифференциалом функции 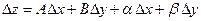 , (19.1)
, (19.1)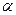 и
и 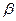 – некоторые функции от
– некоторые функции от 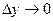 . Выражение
. Выражение 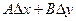 называется полным дифференциалом функции
называется полным дифференциалом функции 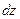 или
или 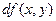 , а его слагаемые
, а его слагаемые 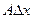 и
и 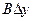 называются частными дифференциалами функции
называются частными дифференциалами функции 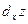 и
и 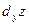 .
.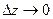 при
при 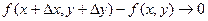 . Следовательно,
. Следовательно, 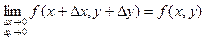 или
или 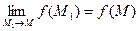 , что и означает непрерывность функции
, что и означает непрерывность функции 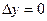 ,
, 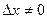 . Тогда
. Тогда 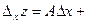
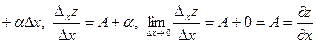 . Аналогично, если
. Аналогично, если 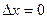 ,
, 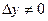 , то
, то 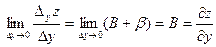 . Так как А и В конечны, то
. Так как А и В конечны, то 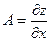 и
и 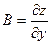 , получим выражение дифференциала через частные производные:
, получим выражение дифференциала через частные производные: 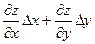 . Отсюда при
. Отсюда при 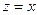 и
и 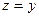 находим
находим 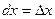 и
и 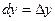 , поэтому
, поэтому 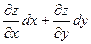 .
.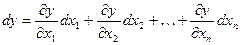 .
.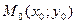 , то в этой точке функция дифференцируема.
, то в этой точке функция дифференцируема.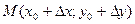 , которая принадлежит указанной окрестности:
, которая принадлежит указанной окрестности: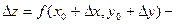
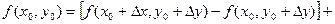
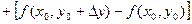 .
.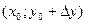 в точку
в точку 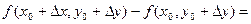
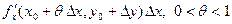 .
.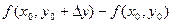
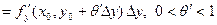 .
.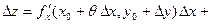
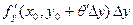 .
.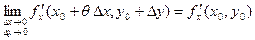 ,
, 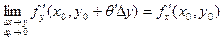 .
.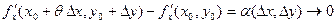 при
при 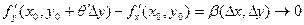 при
при 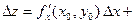
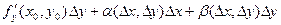 .
. , причем функции
, причем функции 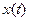 и
и 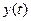 тоже дифференцируемы. Нужно найти производную
тоже дифференцируемы. Нужно найти производную 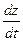 . Пусть аргумент t получает приращение
. Пусть аргумент t получает приращение 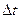 . Тогда х и у получат соответствующие приращения
. Тогда х и у получат соответствующие приращения 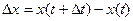 ,
, 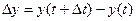 , причем
, причем 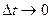 в силу непрерывности дифференцируемой функции. Функция
в силу непрерывности дифференцируемой функции. Функция 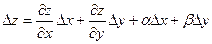 в силу ее дифференцируемости. Отсюда
в силу ее дифференцируемости. Отсюда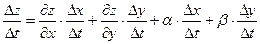 ,
, 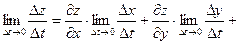
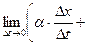
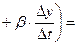
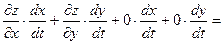
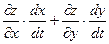 .
.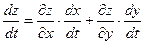 . (19.1)
. (19.1)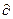 пишется тогда, когда находится частная производная функции по одной из нескольких переменных, знак d – тогда, когда производная находится по основному аргументу, и этот аргумент единственный.
пишется тогда, когда находится частная производная функции по одной из нескольких переменных, знак d – тогда, когда производная находится по основному аргументу, и этот аргумент единственный.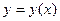 . Тогда основным аргументом является х и формула (19.1) принимает вид
. Тогда основным аргументом является х и формула (19.1) принимает вид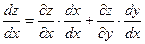
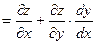 .
.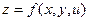 , где
, где 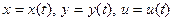 имеем
имеем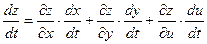 . (19.2)
. (19.2)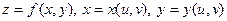 . Здесь уже производные по основным аргументам будут частными производными (их два). Положим
. Здесь уже производные по основным аргументам будут частными производными (их два). Положим 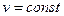 и найдем
и найдем 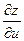 , воспользовавшись формулой (19.1):
, воспользовавшись формулой (19.1):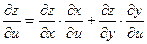 .
.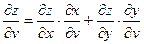 .
.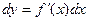 остается неизменной, если заменить независимую переменную х функцией. Имеет ли место это свойство для функции нескольких переменных? Выясним это.
остается неизменной, если заменить независимую переменную х функцией. Имеет ли место это свойство для функции нескольких переменных? Выясним это.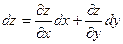 .
.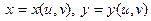 . Поскольку теперь ухе u и v – независимые переменные, имеем
. Поскольку теперь ухе u и v – независимые переменные, имеем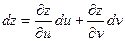 .
.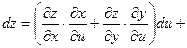
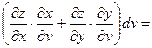
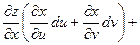
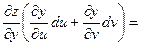
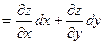 , т.е. формула для вычисления дифференциала сохраняется и в случае, когда х и у – функции. Таким образом, форма дифференциала является инвариантной, т.е. неизменной и для независимых переменных х и у, и для функций х и у.
, т.е. формула для вычисления дифференциала сохраняется и в случае, когда х и у – функции. Таким образом, форма дифференциала является инвариантной, т.е. неизменной и для независимых переменных х и у, и для функций х и у.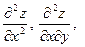
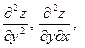 при этом
при этом 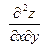 и
и 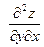 называются смешанными производными. Например, для функции
называются смешанными производными. Например, для функции 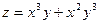
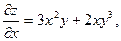
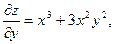
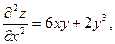
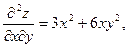
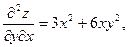
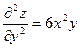 . Аналогично определяются частные производные 3-го, 4-го и т.д. порядка.
. Аналогично определяются частные производные 3-го, 4-го и т.д. порядка.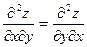 . Всегда ли так будет или это случайное совпадение? Имеет место
. Всегда ли так будет или это случайное совпадение? Имеет место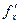 и
и 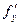 , а также вторые смешанные производные
, а также вторые смешанные производные 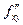 и
и 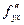 ; 3) производные
; 3) производные 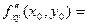
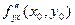 .
.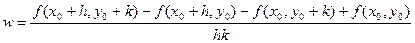 , (19.3)
, (19.3)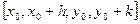 . Пусть
. Пусть 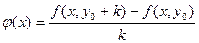 – вспомогательная функция, дифференцируемая на отрезке
– вспомогательная функция, дифференцируемая на отрезке 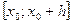 в силу 2-го условия теоремы и, следовательно, непрерывная. Имеем
в силу 2-го условия теоремы и, следовательно, непрерывная. Имеем 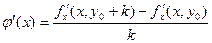 . Выражение (19.3) с помощью
. Выражение (19.3) с помощью 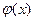 записывается следующим образом:
записывается следующим образом: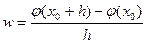 . (19.4)
. (19.4)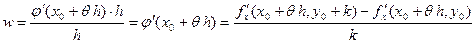 .
.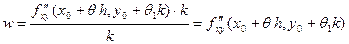 .
.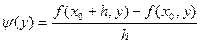
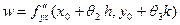 , поэтому
, поэтому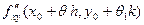 =
= 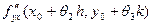 .
.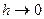 и
и 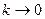 и учитывая, что
и учитывая, что 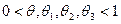 и смешанные производные непрерывны, получим
и смешанные производные непрерывны, получим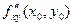 =
= 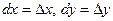 . Зафиксируем
. Зафиксируем 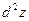 или
или 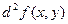 . Таким образом, по определению
. Таким образом, по определению 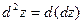 . Учитывая, что
. Учитывая, что 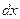 и
и 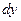 постоянны, находим
постоянны, находим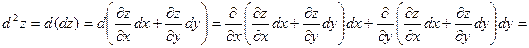
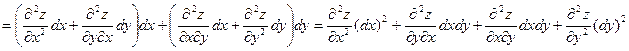 .
.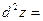
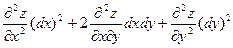 .
.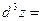
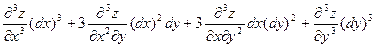 ,
,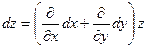 ,
,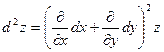 ,
,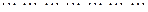
 .
.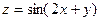 найдем
найдем 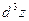 в точке
в точке 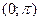 .
.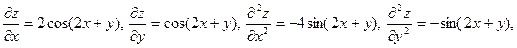
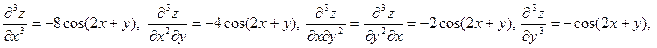
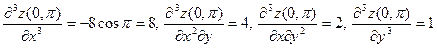
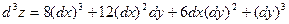 .
.
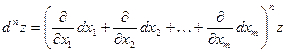 .
.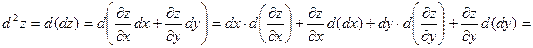
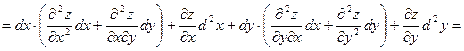
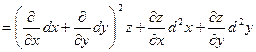 .
.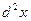 и
и 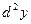 не равны нулю.
не равны нулю.