 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
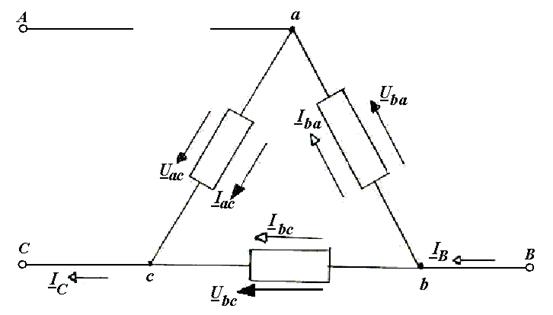
Общие теоретические сведения. Для соединения трехфазного приемника энергии треугольником (рис.11.1) необходимо конец каждой фазы приемника соединить с началом следующей фазы и точкиДля соединения трехфазного приемника энергии треугольником (рис.11.1) необходимо конец каждой фазы приемника соединить с началом следующей фазы и точки соединения фаз подключить тремя линейными проводами к фазам генератора. Положительные направления токов в фазах треугольника принято обозначать по часовой стрелке, т.е. от a к b, от b к c и от c к a.
Рис.11.1. Соединение приемников электрической энергии треугольником. При соединении приемников электрической энергии треугольниками линейные напряжения равны фазным напряжениям:
Токи в фазах определяются по закону Ома:
Составим на основании первого закона Кирхгофа уравнения для узлов a, b и c и выразим из них линейные токи. Они будут равны геометрической разности соответствующих фазных токов:
На рис. 11.2 показаны векторная топографическая диаграмма напряжений и векторная диаграмма токов для симметричной активной нагрузки.
Рис.11.2. Векторная топографическая диаграмма напряжений и векторная диаграмма токов для симметричной активной нагрузки, соединенной треугольником. Построение топографической диаграммы начинается с построения замкнутого треугольника векторов фазных напряжений на приемнике Затем строятся векторы фазных токов При симметричной нагрузке векторы фазных токов равны между собой и образуют симметричную систему токов. По векторам фазных токов строятся векторы линейных токов согласно формуле (11.3). Чтобы построить вектор линейного тока I A, нужно к вектору фазного тока I ab прибавить вектор (- I ca), равный по величине вектору Ica, но направленный в противоположную сторону. Замыкающий вектор будет равен линейному току I A. Аналогично строятся векторы I B и I C. Для симметричной нагрузки линейный ток отстает от фазного на угол 300. Между действующими значениями линейного и фазного токов существует соотношение:
т.е. при симметричной нагрузке линейные токи в При изменении сопротивления в какой-либо фазе приемника произойдет соответствующее изменение тока этой фазы и токов двух линейных проводов, примыкающих к этой фазе. Значения токов в других фазах не изменяются. На рис. 11.3 показаны векторная топографическая диаграмма напряжений и векторная диаграмма токов для случая неравномерной активной нагрузки. Векторы фазных и линейных токов в этом случае находятся по тем же уравнениям (11.2) и (11.3). Порядок построения векторной диаграммы не отличается от предыдущего. Векторная диаграмма построена в предположении, что
Рис.11.3. Векторная топографическая диаграмма напряжений и векторная диаграмма токов для случая неравномерной активной нагрузки. На рис. 11.4 показаны векторная топографическая диаграмма напряжений и векторная диаграмма токов для случая обрыва в фазе ab (Iab =0). Фазные токи
Как видно из (11.6) линейный ток При обрыве линейного провода (
Рис.11.4. Векторная топографическая диаграмма напряжений и векторная диаграмма токов для случая обрыва в фазе ab (Iab =0).
Рис.11.5. Схема соединения треугольником при обрыве линейного провода. При неоднородной нагрузке фазные и линейные токи также находятся по формулам (11.2) и (11.3), но только следует учитывать углы сдвига фаз между фазными напряжениями и токами, которые определяются соотношениями:
Рис.11.6. Векторная диаграмма при обрыве линейного провода. Активная мощность симметричной трехфазной нагрузки равна:
При соединении звездой
Здесь Дата добавления: 2016-03-26 | Просмотры: 659 | Нарушение авторских прав |

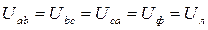 (11.1)
(11.1) ;
;  ;
; 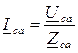 (11.2)
(11.2) (11.3)
(11.3)
 ;
; 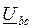 ;
;  .
. ;
;  ;
; 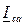 . Для активной нагрузки векторы токов совпадают по фазе с соответствующими векторами напряжений. Начало векторов фазных токов следует совместить с началами векторов соответствующих напряжений на приемнике.
. Для активной нагрузки векторы токов совпадают по фазе с соответствующими векторами напряжений. Начало векторов фазных токов следует совместить с началами векторов соответствующих напряжений на приемнике. , или (11.4)
, или (11.4)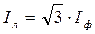 , (11.5)
, (11.5) раз больше фазных токов.
раз больше фазных токов. .
.
 и
и  остаются при этом без изменения. В этом случае линейные токи будут равны:
остаются при этом без изменения. В этом случае линейные токи будут равны: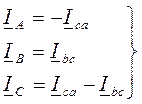 (11.6)
(11.6) не меняется. Изменяются линейные токи в тех линейных проводах, которые примыкают к разомкнутой фазе, т.е. токи
не меняется. Изменяются линейные токи в тех линейных проводах, которые примыкают к разомкнутой фазе, т.е. токи  и
и  .
.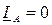 ), например, при перегорании предохранителя в линейном проводе А (рис.11.5) к фазе bc подводится линейное напряжение
), например, при перегорании предохранителя в линейном проводе А (рис.11.5) к фазе bc подводится линейное напряжение  , а фазы ba и ac оказываются включенными последовательно на это напряжение, которое и разделится между ними.
, а фазы ba и ac оказываются включенными последовательно на это напряжение, которое и разделится между ними.
 ;
; 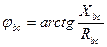 ;
;  (11.7)
(11.7)
 (11.8)
(11.8) и
и  , а при соединении нагрузки треугольником
, а при соединении нагрузки треугольником  и
и  . Следовательно, независимо от вида соединений, активная мощность симметричной трехфазной цепи выражается через линейные напряжение и ток следующим образом:
. Следовательно, независимо от вида соединений, активная мощность симметричной трехфазной цепи выражается через линейные напряжение и ток следующим образом: (11.9)
(11.9) - угол сдвига фазного тока относительно одноименного фазного напряжения. Активная мощность в соответствии с (11.8) можно измерить одним ваттметром, утроив его показания. Для измерения активной мощности при неравномерной нагрузке необходимо иметь три ваттметра для измерения мощности в каждой фазе.
- угол сдвига фазного тока относительно одноименного фазного напряжения. Активная мощность в соответствии с (11.8) можно измерить одним ваттметром, утроив его показания. Для измерения активной мощности при неравномерной нагрузке необходимо иметь три ваттметра для измерения мощности в каждой фазе.