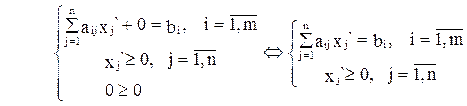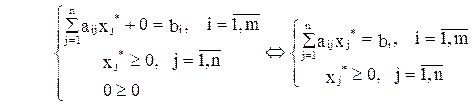|
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Двухэтапный симплекс-метод
1. У больного наблюдается гемипарез, гемигипостезия и гемианопсия справа. Где очаг поражения? а) средний мозг слева б) варольев мост справа в) внутренняя капсула справа г) продолговатый мозг слева д) внутренняя капсула слева.
2. У больного наблюдается прозопарез справа, центральный парез конечностей слева. Где очаг поражения? а) средний мозг слева б) варольев мост справа в) внутренняя капсула справа г) продолговатый мозг слева д) внутренняя капсула слева.
3. У больного наблюдается дисфагия, дисфония, дизартрия, выпадение глоточного рефлекса слева и центральный парез конечностей. Где очаг поражения? а) средний мозг слева б) варольев мост справа в) внутренняя капсула справа г) продолговатый мозг слева д) внутренняя капсула слева.
4. У больного наблюдается расходящееся косоглазие, нарушение движения глазного яблока вверх и вниз слева и центральный парез конечностей справа. Где очаг поражения? а) средний мозг слева б) варольев мост справа в) внутренняя капсула справа г) продолговатый мозг слева д) внутренняя капсула слева.
5. У больного наблюдается нарушение координации в правых конечностях (динамическая атаксия). Где очаг поражения? а) левое полушарие мозжечка б) червь мозжечка в) правое полушарие мозжечка г) задние канатики спинного мозга д) верхняя лобная извилина.
6. У больного наблюдается покачивание в позе Ромберга, атаксическая походка. Где очаг поражения? а) левое полушарие мозжечка б) червь мозжечка в) правое полушарие мозжечка г) задние канатики спинного мозга д) верхняя лобная извилина.
7. Нарушена координация движения нижних конечностей, резко ухудшается при закрытых глазах, кроме того, выявляется нарушение мышечно-суставного чувства. Где очаг поражения? а) левое полушарие мозжечка б) червь мозжечка в) правое полушарие мозжечка г) задние канатики спинного мозга д) верхняя лобная извилина.
8. Больной не может стоять и ходить (астазия – абазия). Где очаг поражения? а) левое полушарие мозжечка б) червь мозжечка в) правое полушарие мозжечка г) задние канатики спинного мозга д) верхняя лобная извилина.
9. У больного выявляется нарушение поверхностной чувствительности справа по проводниковому типу, глубокой чувствительности также по проводниковому типу – слева. Кроме того, слева выявляется центральный парез ноги. Где очаг поражения? а) поперечное поражение спинного мозга ниже шейного утолщения б) половинное (справа) поражение спинного мозга в) половинное (слева) поражение спинного мозга г) конский хвост д) конус спинного мозга.
10. У больного выявляется нижний спастический парапарез, острая задержка мочи, расстройство чувствительности по проводниковому типу. Где очаг поражения? а) поперечное поражение спинного мозга ниже шейного утолщения б) половинное (справа) поражение спинного мозга в) половинное (слева) поражение спинного мозга г) конский хвост д) конус спинного мозга.
11. У больного выявляется периферический парез стоп, императивные позывы к мочеиспусканию, расстройство чувствительности в области промежности и медиальной поверхности бедер. Где очаг поражения? а) поперечное поражение спинного мозга ниже шейного утолщения б) половинное (справа) поражение спинного мозга в) половинное (слева) поражение спинного мозга г) конский хвост д) конус спинного мозга.
12. У больного наблюдается истинное недержание мочи, нарушение чувствительности в области промежности и вокруг синуса. Где очаг поражения? а) поперечное поражение спинного мозга ниже шейного утолщения б) половинное (справа) поражение спинного мозга в) половинное (слева) поражение спинного мозга г) конский хвост д) конус спинного мозга.
Двухэтапный симплекс-метод Пусть задача линейного программирования в канонической форме с неотрицательными свободными членами не содержит полного набора базисных переменных:
В этом случае, для того чтобы применить к ней симплекс-метод, используется метод искусственного базиса. Вводят m неотрицательных переменных у1, у2,.... уm, по одной в каждое уравнение. Эти переменные называют искусственными, и составляют расширенную задачу, имеющую следующий вид*:
В этой задаче имеется m единичных столбцов при искусственных переменных, из которых и состоит искусственный базис.
Лемма. Задача (19) всегда разрешима. Доказательство. Очевидно, что область допустимых планов (ОДП) этой задачи не может быть пуста: налицо хотя бы один допустимый план - тот опорный план, который соответствует исходному базису. В самом деле, план Х = (х1, x2, …, xn, y1, y2, …, ym) = (0, 0, …, 0, b1, b2, …, bm) Î ОДП задачи (19). Целевая функция не может быть не ограничена, так как не может быть меньше нуля (она представляет собой сумму неотрицательных переменных). Лемма доказана.
Пусть U* = (x1*,... xn*, y1*,... ym*) - оптимальный план задачи (19). Теорема о свойствах оптимального плана расширенной задачи: 1). Т.е. если оптимум расширенной задачи положителен (что эквивалентно утверждению о том, что хотя бы одна искусственная переменная в плане U* положительна), то ОДП исходной задачи пуста. 2). Другими словами, если в U* все искусственные переменные равны 0, то план Х(0), составленный из компонент xj* плана U*, является допустимым для исходной задачи.
Доказательство первой части теоремы осуществляется от противного. Предположим, что существует уi* > 0, и ОДП задачи (18) при этом не пуста, т.е. существует план X` = (x1`,.... xn`) Î ОДП задачи (18). Рассмотрим план U` = (x1`,... xn`,
Последняя система истинна, так как X`Î ОДП задачи (18). На плане U` целевая функция задачи (19) Z` = 0 (сумма нулевых искусственных переменных). Однако по условию теоремы, оптимум задачи (19) положителен, т.е. больше Z`. Так как задача (19) на минимум, план U* не может быть оптимальным, если есть допустимый план, на котором значение целевой функции меньше. Мы пришли к противоречию, первая часть теоремы доказана.
Вторая часть теоремы доказывается непосредственно подстановкой U* U* = (x1*,... xn*, 0,... 0) в ограничения задачи (19). Так как этот план допустимый для задачи (19), уравнения системы обращаются в истинные равенства. Они в точности совпадают с уравнениями системы (18) при подстановке в нее плана Х(0) = (x1*,... xn*) (и ограничения неотрицательности также выполняются):
Из выполнения ограничений задачи (19) следует выполнение ограничений задачи (18): следовательно, план Х(0)- допустимый для задачи (18). Теорема доказана.
Смысл доказанной теоремы в том, что решить задачу линейного программирования будет возможно лишь в том случае, если удастся избавиться от всех искусственных переменных*. В самом деле, эти искусственные переменные при построении расширенной задачи были «втиснуты» между левой и правой частями уравнений. На самом деле левые части ограничений были РАВНЫ правым, никакой разницы между ними быть не должно. И задача будет разрешима лишь в том случае, если этот «зазор» - искусственную переменную – удастся свести к нулю во всех ограничениях. Когда искусственные переменные сведены к нулю (выведены из базиса), их можно исключить из рассмотрения. Полученная задача будет отличаться от исходной только целевой функцией (преобразованная система ограничений расширенной задачи будет по сути своей представлять собой преобразованную систему ограничений исходной задачи). Следовательно, останется только перейти к другой целевой функции – задачи (18).
На основании данной теоремы строится алгоритм двухэтапного симплекс-метода, который состоит в следующем: 1-й этап. Строится расширенная задача, которую решают обычным симплекс-методом. 2-й этап. Если оптимум расширенной задачи положителен, делается вывод о неразрешимости исходной задачи, так как ее ОДП = Æ. Если он равен нулю, то переходят к решению симплекс-методом исходной задачи, начиная с опорного плана, соответствующего значениям переменных xj*. Применительно к симплексной таблице этот переход означает, что изменяется столбец сб в соответствии со значениями коэффициентов целевой функции исходной задачи, и пересчитывается критериальная строка: подсчитывают суммы произведений элементов столбцов правой части симплексной таблицы на элементы столбца сб, и во всех столбцах, кроме В, вычитают из этих сумм сj.
При решении задач целесообразно соблюдать следующие рекомендации: а) Если в исходной задаче имеются единичные столбцы при одной или нескольких переменных (т.е. часть базиса), этот факт можно использовать при построении расширенной задачи. А именно, искусственный базис вводится не полностью, а лишь недостающие базисные переменные. При этом при построении целевой функции расширенной задачи минимизируется сумма только искусственных переменных. б) Выбор разрешающего столбца целесообразно осуществлять таким образом, чтобы в первую очередь из базиса выходили искусственные переменные (если это возможно). в) После выхода искусственных переменных из базиса пересчет соответствующих этим переменным столбцов симплексной таблицы не является обязательным. Дата добавления: 2015-01-18 | Просмотры: 1240 | Нарушение авторских прав |

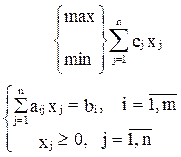

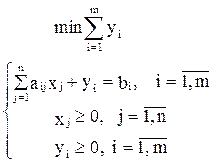
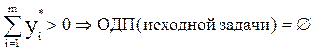
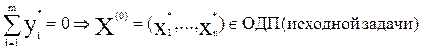
 ) (в нем первые n компонент взяты из плана X`, а все искусственные переменные равны нулю). U`Î ОДП задачи (19), что легко проверить подстановкой его в систему ограничений этой задачи:
) (в нем первые n компонент взяты из плана X`, а все искусственные переменные равны нулю). U`Î ОДП задачи (19), что легко проверить подстановкой его в систему ограничений этой задачи: