 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Пример решения задачи линейного программирования симплекс-методомРешим следующую задачу: max -5х1 + 2х3
-х1 + х3 + х4 £ 5 -3х1 + 5х4 £ 7 х1-4 ³ 0 Приведем ее к канонической форме.
-5х1 - х2 + 2х3 + х5 = 2 -х1 + х3 + х4 + х6 = 5 -3х1 + 5х4 + х7 = 7 х1-7 ³ 0
Теперь пример имеет вид задачи (14) с той разницей, что единичные вектора стоят не при первых трех, а при последних трех переменных - х5, х6 и х7; но изменять обозначения не имеет смысла.
Для удобства дальнейших рассуждений ограничения пронумеруем. При этом обозначим значение целевой функции (-5х1 + 2х3) = z и припишем к системе новое (четвертое) ограничение, после чего задача примет следующий вид:
1) -5х1 - х2 + 2х3 + х5 = 2
3) -3х1 + 5х4 + х7 = 7 4) z + 5х1 - 2х3 = 0 х1-7 ³ 0 Решений такой системы бесконечно много. При последних трех переменных (дополнительных) стоят единичные столбцы: А5 = На этом плане значение целевой функции zо = 0 (-5*0 +
Является ли план Хо оптимальным? Чтобы ответить на этот вопрос, попытаемся увеличить значение целевой функции z. Переменная z входит в ограничение (4). Если в ограничении (4) увеличивать z, то остальные слагаемые (5х1 - 2х3) необходимо уменьшить. Это можно сделать либо за счет уменьшения х1 (при этой переменной стоит положительный коэффициент 5), либо увеличения х3 (при этой переменной стоит отрицательный коэффициент -2). Однако уменьшить переменную х1 нельзя, так как она небазисная и равна нулю (а отрицательные значения переменные задачи принимать не могут). Поэтому следует увеличить х3. Эту переменную увеличить можно, при этом z возрастет. Следовательно, оптимальный план еще не найден. Итак, в следующем опорном плане появится новая ненулевая переменная - х3. Но так как базисных переменных должно быть в этой задаче не более трех, какая-то другая переменная при этом из базиса выйдет, т.е. уменьшится до нуля.
До какого значения можно увеличивать переменную х3, и какую переменную следует вывести из базиса? Чтобы ответить на этот вопрос, следует проанализировать остальные ограничения задачи.
В ограничение (1) входит базисная переменная х5. Если уменьшить ее до нуля, то, учитывая, что небазисные переменные х1 = х2 = 0, получим 2х3 = Аналогично ограничение (2) позволяет увеличить х3 до 5 (за счет уменьшения х6). В ограничение (3) переменная х3 вообще не входит, следовательно, оно позволяет увеличивать значение этой переменной до бесконечности.
Таким образом, самым жестким ограничением является первое, и мы увеличим х3 только до 1 (если попытаться увеличить эту переменную до большего значения, то придется уменьшить переменную х5 до отрицательных значений, иначе ограничение (1) не будет выполняться). Следовательно, в в новом опорном плане переменная х3 станет базисной, а х5 из базиса выйдет. Преобразуем систему методом Гаусса таким образом, чтобы перейти к новому опорному плану. В новой системе столбец коэффициентов при х3 станет единичным, причем единица должна стоять именно в первом ограничении, а в остальных – нули (тогда при ненулевых компонентах опорного плана снова будут линейно независимые столбцы коэффициентов - единичные).
Столбец коэффициентов при х3 будем называть разрешающим (ведущим, ключевым). Так же будем называть и первое ограничение, которое определило выбор переменной, выходящей из базиса. Коэффициент в этом ограничении в разрешающем столбце (он равен 2) будем называть разрешающим элементом.
Чтобы получить на месте разрешающего элемента единицу, надо обе части первого ограничения разделить на этот элемент, т.е. на 2. После этого ограничение примет вид (1`). В ограничение (2) переменная х3 входит с коэффициентом 1. На месте этого коэффициента необходимо получить ноль. Для этого вычтем из ограничения (2) ограничение (1`), в которое х3 входит теперь именно с коэффициентом 1. Результат обозначим (2`). Ограничение (3) можно оставить без изменений, так как коэффициент при х3 в нем и так нулевой. В новой системе обозначим его (3`). В ограничение (4) переменная х3 входит с коэффициентом -2. Умножим обе части ограничения (1`) на -2. Теперь переменная х3 входит в него не с коэффициентом 1, а с коэффициентом -2. Вычтем из уравнения (4) полученное уравнение, при этом коэффициент при х3 станет нулевым. Результат обозначим (4`).
1`) -2,5х1 – 0,5х2 + х3 + 0,5х5 = 1
3`) -3х1 + 5х4 + х7 = 7 4`) z – х2 + х5 = 2 х1-7 ³ 0 Этой системе можно поставить в соответствие новый опорный план, приравняв базисные переменные х3, х6 и х7 к свободным членам, а остальные – к нулю: Х(1) = (0; 0; 1; 0; 0; 4; 7). Значение целевой функции увеличилось: z(1) = 2. Это число является свободным членом ограничения (4`). В самом деле, так как небазисные переменные х2 = х5 =0, то из (4`) z = 2 (z - 0 + 0 = 2). Подстановкой плана в целевую функцию можно получить тот же результат
Из ограничения (4`) видно, что план Х(1) тоже не является оптимальным. Значение z можно еще увеличить за счет увеличения х2. Чтобы определить, до какого значения можно увеличить переменную х2, и какую переменную следует вывести из базиса, снова по очереди рассмотрим ограничения.
В ограничение (1`) х2 входит с отрицательным коэффициентом -0,5. Следовательно, при увеличении х2 значение базисной переменной х3, входящей в это ограничение, тоже будет увеличиваться (и это увеличение может происходить до бесконечности). В ограничение (2`) входит базисная переменная х6. Если уменьшить ее до нуля, то, учитывая, что небазисные переменные х1 = х4 = х5 = 0, получим 0,5х2 = 4 Û х2 = 4/0,5 = 8. Следовательно, ограничение (2`) позволяет увеличить х2 до 8 (за счет уменьшения х6). В ограничение (3`) переменная х2 вообще не входит, следовательно, и оно позволяет увеличивать значение этой переменной до бесконечности.
Таким образом, самым жестким ограничением является второе, и мы увеличим х2 до 8. Следовательно, в новом опорном плане переменная х2 станет базисной, а х6 из базиса выйдет. Снова преобразуем систему методом Гаусса таким образом, чтобы столбец коэффициентов при х2 стал единичным, причем единица должна стоять во втором ограничении (разрешающим столбцом будет столбец коэффициентов при х2, а разрешающим ограничением – второе; разрешающий элемент равен 0,5). Для этого обе части ограничения (2`) разделим на 0,5 (результат обозначим (2``)). Из ограничения (1`) вычтем уравнение (2``), умноженное на (-0,5) (поскольку в ограничении (1`) в разрешающем столбце стоит именно Третье ограничение оставим без изменений, обозначив (3``) (поскольку х2 в это ограничение не входит).
1``) -х1 + х3 + х4 + х6 = 5
3``) -3х1 + 5х4 + х7 = 7 4``) z + 3х1 + 2х4 + 2х6 = 10 х1-7 ³ 0 Этой системе можно поставить в соответствие новый опорный план Х(2) = (0; 8; 5; 0; 0; 0; 7). Значение целевой функции увеличилось: z(2) = 10. Из ограничения (4`) видно, что значение целевой функции увеличить больше нельзя. Для этого пришлось бы уменьшить значения переменных х1, х4 или х6, а они и так равны нулю. Следовательно, Х(2) – оптимальный план, а 10 – оптимум задачи. 3.2.2 Решение задачи в общем виде. Симплексная таблица Вернемся к решению задачи в общем виде из раздела 3.2, начиная с исходного опорного плана Х = (b1, b2,... bm,
Для применения симплекс-метода к системе необходимо приписать еще одно ограничение - критериальное: z -
В решенном примере это было четвертое ограничение. Поскольку в этом примере базисные переменные исходного опорного плана (х5-7) не входили в целевую функцию, то и в критериальное ограничение они не вошли. В общем случае это не так. Например, если бы задача имела вид: max -5х1 + 2х3
1,5х1 + 0,5х2 + х4 - 0,5х5 + х6 = 4 -3х1 + 5х4 + х7 = 7 х1-7 ³ 0 то в качестве базисных в исходном опорном плане следовало бы взять переменные х3, х6 и х7. Одна из них - х3 - входит в целевую функцию. Уравнение z - Чтобы избежать этого, выразим базисную переменную х3 из первого ограничения через небазисные (-2,5х1 – 0,5х2 + х3 + 0,5х5 = 1 Û х3 = 1 +
Итак, в общем случае после введения критериального ограничения столбцы при базисных переменных могут перестать быть единичными. Чтобы избежать этого, выразим базисные переменные x1-m из ограничений через небазисные: x1 = b1 - a1 m+1xm+1 -... -a1 nxn … x i = b i - a i m+ 1xm+ 1 -... -a i nxn … xm = bm - am m+1xm+1 -... -am nxn
и подставим их в целевую функцию: z = После приведения подобных членов и переноса свободного члена в правую часть критериальное ограничение примет следующий вид: z + xm+1(c1a1 m+1 +... + cmam m+1 - c m+1) +... + xn(c1a1 n+... + cmam n - cn) = c1b1 + Обозначим коэффициенты при переменных xj в критериальном ограничении - Dj = Отметим, что коэффициенты при базисных переменных в критериальном ограничении будут нулевыми, что и требовалось получить. Но и эти нулевые коэффициенты также можно рассчитать по формулам ( Таким образом, критериальное ограничение примет вид: z +
Теперь исходные данные задачи линейного программирования можно записать в виде симплексной таблицы (таблица 7). Каждая строка таблицы соответствует одному ограничению задачи линейного программирования ((m+1)-я строка - критериальному ограничению). Левая часть таблицы (первые три столбца) является вспомогательной - в ней в первом столбце указывается номер строки, во втором (xб) - базисная переменная, соответствующая каждой строке (та, которая входит в это ограничение с коэффициентом 1), в третьем (сб) - коэффициент целевой функции при соответствующей базисной переменной. В правой части таблицы в столбце В указаны свободные члены системы ограничений (в (m+1)-ой строке - значение целевой функции на опорном плане d), а все остальные столбцы соответствуют переменным задачи линейного программирования, и в них указаны коэффициенты при этих переменных в каждом ограничении. Над обозначениями переменных в верхней части таблицы рекомендуется указывать соответствующие коэффициенты целевой функции.
Таблица 7 – Симплексная таблица
Идея дальнейшего решения заключается в том, чтобы в критериальном ограничении увеличивать первое слагаемое (z) за счет уменьшения суммы остальных (свободный член - постоянная величина). При этом в той сумме, которую необходимо уменьшить, отличные от нуля коэффициенты стоят только при небазисных переменных (так как базисным соответствуют единичные столбцы). Небазисные переменные равны нулю, их значения можно только увеличивать. При этом увеличиваться должны значения тех небазисных переменных, при которых стоят отрицательные коэффициенты Dj (чтобы сумма уменьшалась). Однако увеличение этих переменных ограничивается другими уравнениями системы.
Лемма 1 (критерий оптимальности плана).Если все Dj ³ 0, то текущий опорный план - оптимальный. Доказательство следует из того, что небазисные переменные равны нулю. Их можно только увеличивать, при этом, так как Dj ³ 0, то целевая функция уменьшается, так как в уравненим (z +
Рассмотрим исходную симплексную таблицу для решенного выше примера (таблица 8). Поскольку для расчетов предполагается использовать средства электронной таблицы Microsoft Excel, слева и сверху от таблицы 8 указаны номера строк и столбцов электронной таблицы. В диапазон ячеек D1:К5 введены исходные данные примера. Исходя из них, заполнена вспомогательная часть таблицы в А2:С5. В D6 введена формула =-D1, которая затем скопирована по строке до К6 (таким образом введены свободный член и коэффициенты критериального ограничения).
Таблица 8 – Исходная симплексная таблица
Таким образом, в таблице 8 записана система (15).
Итак, если все Dj ³ 0, то задача решена (это критерий оптимальности для задачи на максимум). Если это не так, необходимо перейти к другому опорному плану. Для этого выберем столбец таблицы, в котором нарушен критерий оптимальности, т.е. некоторый k-й столбец, такой, что Dk < 0. Этот столбец называют разрешающим (очевидно, он не базисный, так как иначе было бы Dk = 0). Преобразуем симплексную таблицу таким образом, чтобы переменная хк вошла в базис (т.е. в набор базисных переменных), а некоторая другая переменная из него вышла.
В этом примере среди коэффициентов Dj есть отрицательный: D3 = -2 < 0 (k = 3). Поэтому при преобразовании системы (15) в систему (16) в базис входила переменная x3. Далее в разделе 3.2.1 мы определяли, какую переменную следует вывести из базиса, и для этого подсчитывали отношения 2/2 и 5/1.
Для выбора переменной, которая должна выйти из базиса, для всех положительных элементов k-го столбца подсчитывают отношения bi/aiк и выбирают из них наименьшее. Соответствующую строку (пусть это будет
В таблице 8 положительные aiк = ai3 находятся в первой и второй строках. Наименьшее из отношений bi/aiк соответствует первой строке: min {b1/a13; b2/a23 } = {2/2; 5/1} = {1; 5} = 1. Таким образом, разрешающая строка - первая, т.е. t = 1. Разрешающий элемент аtk = а13 = 2. В таблице 8 он выделен заливкой. При преобразовании системы (15) в систему (16) из базиса выходила переменная x5, которая соответствует первой строке.
Левая (вспомогательная) часть новой таблицы будет отличаться только содержанием t-й строки столбцов хб и сб: вместо хt и сt там будет стоять соответственно хк и ск, так как переменная хt из базиса выйдет, а хк войдет. Правая часть таблицы подвергнется преобразованию методом Гаусса. Цель преобразования - получить единичный столбец при переменной хк, причем единица должна будет стоять на месте разрешающего элемента, т.е. в t-ой строке. Общие формулы для таких преобразований выглядят следующим образом (со штрихом обозначены элементы новой таблицы): аtj`= аtj / аtk; bt`= bt / аtk – вся разрешающая строка делится на разрешающий элемент, при этом на его месте получают 1; аij`= аij - аtj`* аik = аij - аtj * аik / аtk; bi`= bi - bt`* аik = bi - bt * аik / аtk – из всех остальных строк вычитают преобразованную разрешающую строку, умноженную на элемент, стоящий в преобразуемой строке в разрешающем столбце (при этом на его месте получают 0, так как из него вычитают его же, умножив на 1); Dj `= Dj - аtj`* Dk =Dj - аtj *Dk / аtk ; d`= d - bt`*Dk = d - bt * Dk / аtk – то же самое делают с критериальной строкой.
Докажем, что при применении этих формул мы действительно сможем построить новый план по тому же правилу (приравняв базисные переменные к свободным членам). Для этого нужно, чтобы новые свободные члены оказались неотрицательными, иначе такой план не будет допустимым. Лемма 2 (о критерии допустимости таблицы). При преобразовании таблицы она сохраняет допустимость, т.е. bi` ³ 0, "i. Дата добавления: 2015-01-18 | Просмотры: 921 | Нарушение авторских прав |
 -5х1 - х2 + 2х3 £ 2
-5х1 - х2 + 2х3 £ 2 max -5х1 + 2х3
max -5х1 + 2х3 max z
max z 2) -х1 + х3 + х4 + х6 = 5
2) -х1 + х3 + х4 + х6 = 5 , А6 =
, А6 =  и А7 =
и А7 =  . Поэтому удобно взять переменные х5, х6 и х7 в качестве базисных. Приравняем их к свободным членам, а остальные – к нулю. Таким образом мы получим исходный опорный план - одно из решений этой системы - Хо =
. Поэтому удобно взять переменные х5, х6 и х7 в качестве базисных. Приравняем их к свободным членам, а остальные – к нулю. Таким образом мы получим исходный опорный план - одно из решений этой системы - Хо = - она входит только в ограничение (4) с коэфициентом 1). Она тоже приравнивается к свободному члену – 0.
- она входит только в ограничение (4) с коэфициентом 1). Она тоже приравнивается к свободному члену – 0.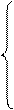 Преобразованная система примет вид:
Преобразованная система примет вид: 2`) 1,5х1 + 0,5х2 + х4 - 0,5х5 + х6 = 4
2`) 1,5х1 + 0,5х2 + х4 - 0,5х5 + х6 = 4 Из ограничения (4`) вычтем уравнение (2``), умноженное на (-1) (поскольку в ограничении (4`) в разрешающем столбце стоит именно
Из ограничения (4`) вычтем уравнение (2``), умноженное на (-1) (поскольку в ограничении (4`) в разрешающем столбце стоит именно  2``) 3х1 + х2 + 2х4 - х5 + 2х6 = 8
2``) 3х1 + х2 + 2х4 - х5 + 2х6 = 8 ). Обозначим z целевую функцию задачи. На исходном плане значение целевой функции
). Обозначим z целевую функцию задачи. На исходном плане значение целевой функции  , так как слагаемые, соответствующие небазисным переменным, обратятся в 0.
, так как слагаемые, соответствующие небазисным переменным, обратятся в 0. = 0.
= 0. -2,5х1 – 0,5х2 + х3 + 0,5х5 = 1
-2,5х1 – 0,5х2 + х3 + 0,5х5 = 1 = c1(b1 -
= c1(b1 -  - cm+1) + … + xn(
- cm+1) + … + xn(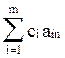 - cn) =
- cn) =  .
. - cj; а свободный член этого ограничения - d =
- cj; а свободный член этого ограничения - d =  .
. = d
= d