 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Доказательство
Свободные члены вычисляются по формулеbi`= bi - bt * аik / аtk. Здесь bi, bt ³ 0 (т.к. предыдущая таблица – допустимая); аtk > 0 (по способу выбора разрешающего элемента). Если аik £ 0, то bi` ³ 0 (к неотрицательному числу прибавляют неотрицательное). Если аik > 0, то разделим обе части неравенства bi - bt * аik / аtk ³ 0 на аik. Получим: bi - bt * аik / аtk ³ 0 Û bi / аik - bt / аtk ³ 0 Û bi / аik ³ bt / аtk Последнее неравенство истинно по способу выбора разрешающего элемента. Следовательно, будет истинно и первое из этих трех неравенств, т.е. bi` ³ 0. Лемма доказана. Таким образом, при правильном выборе разрешающего элемента преобразованной системе уравнений по-прежнему можно поставить в соответствие опорный план так же, как это делалось для исходной таблицы. Лемма 3 (об изменении значения целевой функции). При переходе к следующему опорному плану значение целевой функции не убывает: d`³ d. Доказательство. Новое значение целевой функции вычисляется по формулеd`= d - bt * Dk / аtk. Здесь аtk > 0, Dk < 0, bt ³ 0. Если bt > 0, то d`> d. Есди bt = 0, то d`= d. Лемма доказана.
Лемма 4 (о неограниченности целевой функции). Если в разрешающем столбце нет возможности выбрать разрешающий элемент (нет положительных элементов, все аik £ 0), то целевая функция задачи линейного программирования не ограничена. Доказательство. Пусть Dk < 0, все аik £ 0. Хо = (b1,...,bm, 0,..., 0) - исходный опорный план; k-я переменная - небазисная. Рассмотрим семейство планов:
Эти планы допустимые. В самом деле, так как все аik £ 0, все переменные здесь неотрицательные. В выполнении остальных ограничений легко убедиться, подставив эти планы в систему ограничений задачи (14). В самом деле, в каждом ограничении при этом будет получено: bi – aik*a + aik*a = bi Последнее ограничение будет иметь вид: z + z + Dk*a = d; z = d - Dk*a. Так как Dk <0, a®+µ Þ z®+µ (при стремлении к бесконечности значение целевой функции тоже будет стремиться к плюс бесконечности). Таким образом, на допустимых планах целевая функция может принимать неограниченно большие значения. Лемма доказана. Теорема о сходимости симплекс-метода. Если после каждого этапа симплекс-метода значение целевой функции возрастает, то алгоритм дает решение задачи линейного программирования в конечное число шагов. Доказательство. На каждом этапе мы получаем текущий опорный план (вершину ОДП). Число опорных планов конечно (не больше, чем число способов выбора m переменных из n -
Целевая функция не убывает по лемме 3. Если ее значение не изменяется, то возможно зацикливание (хотя оно встречается довольно редко). В систему может быть вставлен специальный блок для проверки на зацикливание. По той же лемме 3 значение целевой функции может не измениться только если bt = 0, т.е. в очередном опорном плане базис был вырожденным.
Из формулы для пересчета целевой функции (d`= d - bt * Dk / аtk) следует, что при выборе разрешающего столбца можно заранее определить, на сколько изменится ее значение: на Dk * bt / аtk. Следовательно, если критерий оптимальности нарушен не в одном, а в нескольких столбцах таблицы, то выбрать в качестве разрешающего лучше тот из них, для которого это изменение будет больше. Тогда решение задачи может быть получено быстрее, за меньшее число этапов.
Вторая симплексная таблица для решенного примера примет вид таблицы 9. Для того, чтобы получить ее в Microsoft Excel, следует скопировать диапазон ячеек А1:К6 на диапазон А7:К11. Затем отредактируем вспомогательную часть таблицы: в В8 вместо x5 введем x3, а в С8 вместо 0 введем 2. Затем отредактируем диапазон D8:К11. Для этого в D8 введем формулу =D3/$G3*. Она вводится для того, чтобы обе части третьего ограничения разделить на G3, т.е. на 2. В D9 введем формулу =D4-D$8*$G4. Скопируем последнюю формулу на диапазон ячеек D10:D11. В результате в D10 появится формула =D5-D$8*$G5, а в D11 формула =D6-D$8*$G6. Это делается для того, чтобы из всех остальных строк, кроме разрешающей, вычесть преобразованную разрешающую (она в 8-й строке электронной таблицы), умноженную соответственно на 1 (в G4), 0 (в G5) и -2 (в G6). Выделим формулы в диапазоне D8:D11 и скопируем их на диапазон ячеек Е8:К11. В результате столбец коэффициентов при x3 станет единичным.
Таблица 9 – Вторая симплексная таблица
Таким образом, в таблице 9 записана система (16).
Отметим, что для пересчета критериального ограничения можно использовать два способа: а) описанный выше метод Гаусса (поскольку это такое же линейное ограничение, как и остальные m ограничений); б) можно заново перестроить его по выведенным ранее формулам Dj = При использовании для расчетов электронной таблицы способ (а) предпочтительнее.
Тем не менее, если ввести в D11 другую формулу =СУММПРОИЗВ($C8:$C10;D8:D10)-D1, и именно ее скопировать по строке до К11, то результат вычислений получится тем же самым, что приведен в таблице 9. В самом деле, d = 2*1 + 0*4 + 0*7 – 0 = 2 (здесь, в отличие от других столбцов, вычитать 0 не обязательно, но ячейка D1 все равно нулевая); D1 = 2*(-2,5) + 0*1,5 + 0*(-3) – (-5) = 0; D2 = 2*(-0,5) + 0*0,5 + 0*0 –
Если в исходной симплексной таблице базисные переменные входят в целевую функцию, то в ней построить критериальную строку можно только способом (б).
В таблице 9 критерий оптимальности нарушен в столбце коэффициентов при x2. Положительный коэффициент в этом столбце только один – 0,5. Это разрешающий элемент, в таблице 9 он выделен. Следовательно, x2 войдет в базис вместо x6. В результате преобразований будет получена таблица 10. Для того, чтобы получить эту таблицу, диапазон ячеек А7:К11 скопируем на диапазон А12:К16. В В14 вместо x6 введем x2. Затем отредактируем диапазон D13:К16. Для этого в D14 введем формулу =E9/$F9. Она вводится для того, чтобы обе части второго (разрешающего) ограничения разделить на F9, т.е. на 0,5. В D13 введем формулу =D8-D$14*$F8. Скопируем последнюю формулу на диапазон ячеек D15:D16. Это делается для того, чтобы из всех остальных строк, вычесть преобразованную разрешающую, умноженную соответственно на -0,5, 0 и -1. Выделим формулы в диапазоне D13:D16 и скопируем их на диапазон ячеек Е13:К16. В результате столбец коэффициентов при x2 станет единичным. Тот же результат был бы получен, если бы в D16 вместо формулы =D11-D$14*$F11 стояла формула =СУММПРОИЗВ($C13:$C15;D13:D15)-D1, и именно она была бы скопирована на диапазон Е16:К16.
Таблица 10 – Оптимальная симплексная таблица
Таким образом, в таблице 10 записана система (17).
В критериальном ограничении последней симплексной таблицы нет отрицательных коэффициентов. Следовательно, оптимальный план найден. А именно, небазисные переменные x1 = x4= x5 = x6 = 0, а базисные (их список находится в столбце xб) равны свободным членам (в столбце В): x3 = 5, x2 = 8, x7 = 7. Оптимум равен 10. Итак, Х(*) = Х(2) = (0; 8; 5; 0; 0; 0; 7), z(*) = z(2) = 10.
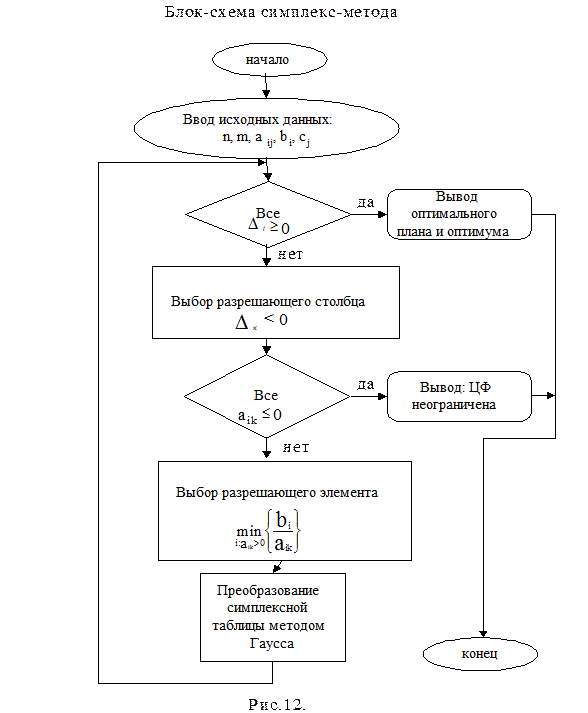
Алгоритм симплекс-метода можно представить в виде блок-схемы, приведенной на рисунке 26.
Рисунок 26 – Блок-схема симплекс-метода Решение задачи на минимум отличается только критерием оптимальности - все коэффициенты критериального ограничения должны быть неположительны (соответственно, разрешающий столбец выбирается по положительному элементу).
При решении задач целесообразно соблюдать следующие рекомендации: а) Если среди ограничений задачи линейного программирования имеются неравенства, или не все переменные являются неотрицательными, начните решение с приведения задачи к канонической форме. Проверьте, все ли свободные члены неотрицательны, и имеется ли базис. Если нет, проверьте, нельзя ли этого добиться простыми преобразованиями. б) Чтобы избежать ошибки, разрешающий элемент в таблице следует выделять. в) На каждой итерации симплекс-метода целесообразно проверять, соблюдены ли в таблице следующие элементарные правила: 1) Не должен нарушаться критерий допустимости. Отрицательный элемент в столбце В - признак ошибки в расчетах, причем скорее всего она была допущена при выборе разрешающей строки. 2) Должен присутствовать полный набор единичных столбцов при базисных переменных, причем единица должна стоять в той строке, которой эта переменная соответствует, а в остальных - нули. 3) Одно из средств контроля правильности вычислений - подсчет критериальной строки двумя способами: методом Гаусса и через сумму произведений (результаты должны совпадать). 4) При переходе к следующей симплексной таблице значение целевой функции должно, по крайней мере, не убывать (если задача на максимум) или не возрастать (если она на минимум). Несоблюдение этих правил лишает смысла все остальные действия. г) Из заключительной симплексной таблицы необходимо извлечь решение задачи линейного программирования или указать, почему она неразрешима. 3.3 Решение задачи производственного планирования симплекс-методом Решим симплекс-методом задачу из раздела 1.1. Для этого вначале нужно привести ее к канонической форме. Это было сделано в разделе 1.4.1. В такой задаче есть готовый базис: переменные x3, x4 и x5. Исходная симплексная таблица примет вид таблицы 11 (столбцы J и К предназначены для вспомогательных расчетов).
Таблица 11 – Исходная симплексная таблица для задачи производственного планирования
Критерий оптимальности нарушен в двух столбцах x1 и x2. Следовательно, чтобы увеличить значение прибыли, надо увеличить (включить в базис) любую из этих переменных. Если выбрать переменную x1, то разрешающим элементом будет а11, так как min {800/0,8; 600/0,2; 120/0,01} = min {1000; 3000; 12000} = 1000. Тогда прибыль возрастет на 1000*108 = 108000. Если выбрать переменную x2, то разрешающим элементом будет а32, так как min {800/0,5; 600/0,4; 120/0,1} = min {1600; 1500; 1200} = 1200. Тогда прибыль возрастет на 1200*140 = 168000. Так как 168000 > 108000, лучше ввести в базис x2. Описанные расчеты нет необходимости осуществлять вручную. Можно, например, ввести в J3 формулу =$D3/E3, а затем скопировать ее на К3 и J4:К5. В результате в диапазоне ячеек J3:К5 будут получены те отношения, из которых выбирается наименьшее. Если бы какой-либо из коэффициентов в столбцах Е и F был неположительным, то в столбцах J и К появилось бы отрицательное число или сообщение о попытке деления на ноль. Выбрать наименьшее из положительных отношений в такой задаче можно вручную. Затем в J6 можно ввести формулу =$D3/E3, а в К6 - =F6*K5. Результаты вычислений приведены в таблице 11. Для вспомогательных расчетов можно использовать любые свободные ячейки.
Итак, в базис войдет x2, при этом из базиса выходит x5, и таблица примет вид таблицы 12 (обе части третьего ограничения делят на 0,1; а из остальных трех строк вычитают преобразованное третье ограничение, умноженное соответственно на 0,5; 0,4 и -140).
Таблица 12 – Вторая симплексная таблица для задачи производственного планирования
Здесь критерий оптимальности нарушен только в одном столбце - x1. Так как min {200/0,75; 120/0,16; 1200/0,1} = min {266 2/3; 750; 12000} =
Таблица 13 – Оптимальная симплексная таблица для задачи производственного планирования
Таблица оптимальна, так как в критериальной строке нет отрицательных коэффициентов. Из таблицы видно, что решением задачи будет Х* = (266,67; 1173,3; 0; 77,333; 0), z*=19306,7. Если изменить формат ячеек на дробный, то ответ совпадет с полученным в разделе 2.1. Ответ задачи: кондитерской фабрике следует выпускать 266,7 т карамели «Снежинка» и 1173,3 т карамели «Яблочная». При этом сахарный песок и фруктовое пюре будут израсходованы полностью (так как x3 = x5 =0), а остаток патоки составит 77,3 т. Максимальная прибыль составит Вопросы и упражнения 1 Дайте определение опорного плана задачи линейного программирования. 2 В чем заключается идея симплекс-метода? 3 Как строится симплексная таблица? 4 Сформулируйте критерий оптимальности симплексной таблицы. 5 Сформулируйте критерий допустимости симплексной таблицы. 6 Сформулируйте правило выбора разрешающего элемента. 7 Сформулируйте признак неограниченности целевой функции (по симплексной таблице). 8 Может ли задача линейного программирования, удовлетворяющая условиям, перечисленным в разделе 3.2, быть неразрешимой по причине того, что ее ОДП пуста? 9 Если критерий оптимальности нарушен в нескольких столбцах, в чем заключается способ выбора разрешающего столбца, при котором решение может быть получено быстрее? 10 Нельзя ли найти способ (и в чем он заключается) определения по заключительной симплексной таблице того, является ли полученное решение единственным? 11 Решите симплекс-методом следующие задачи:
12 Решите симплекс-методом задачу 9 из раздела 1.5. * Симплекс представляет собой выпуклую оболочку m+1 аффинно независимых точек в m-мерном пространстве (т.е. пересечение всех выпуклых множеств, содержащих эти точки). Не приводя здесь определение аффинной независимости, ограничимся утвержением, что в m-мерном пространстве таких точек может быть не больше m+1. Можно сказать, что любой треугольник на плоскости (в двумерном пространстве) - симплекс. Название метода связано с тем, что изначально он был разработан для задачи, ОДП которой представляло собой так называемый стандартный симплекс (определялось ограничениями; xi ³ 0, i=1,n). На плоскости это треугольник с вершиной в начале координат и точках (0;1) и (1;0).
* Вектора А1... Аn называются линейно независимыми, если не существует таких чисел d1... dn, не равных одновременно нулю, при которых djАj = 0.
* Число сочетаний из n по m рассчитывается по формуле. * Знак $ при вводе формул в Microsoft Excel означает абсолютную ссылку. В дальнейшем при копировании формулы номер столбца или строки, перед которыми стоит этот знак, не будет изменяться. Дата добавления: 2015-01-18 | Просмотры: 1540 | Нарушение авторских прав |
 Х(a) = (b1 - a1ka, b2 - a2ka,...,bm - amka, 0,..., 0, a, 0,...,0), a ³ 0.
Х(a) = (b1 - a1ka, b2 - a2ka,...,bm - amka, 0,..., 0, a, 0,...,0), a ³ 0. = d. Подставим в него план Х(a). При этом все слагаемые при небазисных переменных, кроме –го, обратятся в ноль (при небазисных тоже, потому что при этих переменных коэффициенты в критериальном ограничении равны нулю).
= d. Подставим в него план Х(a). При этом все слагаемые при небазисных переменных, кроме –го, обратятся в ноль (при небазисных тоже, потому что при этих переменных коэффициенты в критериальном ограничении равны нулю). *). Так как по предположению целевая функция возрастает, то мы второй раз не получим пройденный план, а значит, в конечное число этапов получим решение.
*). Так как по предположению целевая функция возрастает, то мы второй раз не получим пройденный план, а значит, в конечное число этапов получим решение.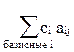 - cj; d =
- cj; d =  (по своей сути это означает выражение базисных переменных из ограничений через небазисные и подстановку их в критериальное ограничение).
(по своей сути это означает выражение базисных переменных из ограничений через небазисные и подстановку их в критериальное ограничение).

 Пример 1.
max -4х1 + 3х2 - 3х3
-2х1 + х2 + х3 = 1
х1 - 3х2 - х4 = -13
4х1 + х2 + х5 = 26
-х1 - 3х2 ³ -6
х1-5 ³ 0
Пример 1.
max -4х1 + 3х2 - 3х3
-2х1 + х2 + х3 = 1
х1 - 3х2 - х4 = -13
4х1 + х2 + х5 = 26
-х1 - 3х2 ³ -6
х1-5 ³ 0
 Пример 3.
max 5х2 - 2х4
Пример 3.
max 5х2 - 2х4
 4х1 + 10х2 - 5х3 £ 7
х1 - 3х2 + 2х3 + х4 ³ 4
3х1 - 8х2 £ 12
х1-4 ³ 0
4х1 + 10х2 - 5х3 £ 7
х1 - 3х2 + 2х3 + х4 ³ 4
3х1 - 8х2 £ 12
х1-4 ³ 0