 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Доказательство. В силу условий теоремы и соотношения Чепмена-Колмогорова, имеем
Отсюда следует, что:
Доказательство закончено. 5.2.2. Аналогичным образом можно вывести прямые уравнения Колмогорова. Пусть
Переходя к пределу когда
Из (23a), в частности, следует, что для удовлетворяет прямому уравнению Колмогорова
5.2.3. Замечания. 1) В §14 главы 3 мы уже вывели прямое уравнение Колмогорова (23) при более слабых предположениях, опираясь на теорию точечных случайных процессов. 2) В §15 главы 3 нами были получены условия разрешимости уравнения Колмогорова (23). 5.3. Приведем без доказательства один результат, касающийся однородных МПШ с конечным или счетным числом состояний. Теорема 3. Пусть
причем, 1) если 3) Замечание. Для однородных МПШ с конечным или счетным числом состояний с помощью матрицы 1) состояние i называется мгновенным, если 2) состояние i называют регулярным, если
Дата добавления: 2015-01-18 | Просмотры: 840 | Нарушение авторских прав |
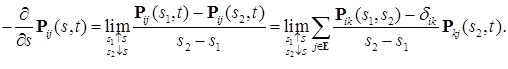
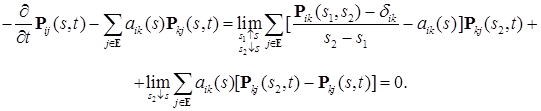
 Из (19) следует, что при
Из (19) следует, что при  справедливо равенство
справедливо равенство . (23)
. (23) и
и  в (23), имеем
в (23), имеем (23a)
(23a)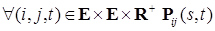
 (24)
(24) – однородный МПШ с конечным или счетным числом состояний. Тогда существуют конечные или бесконечные пределы
– однородный МПШ с конечным или счетным числом состояний. Тогда существуют конечные или бесконечные пределы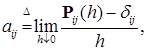
 , то
, то  – конечно; 2)
– конечно; 2)  либо конечно, либо
либо конечно, либо  ;
;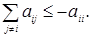
 размера
размера  можно произвести следующую классификацию состояний:
можно произвести следующую классификацию состояний: ), его называют задерживающим;
), его называют задерживающим; (нерегулярным, если
(нерегулярным, если  ), причем, если все состояния регулярны, то однородный МПШ называется консервативным.
), причем, если все состояния регулярны, то однородный МПШ называется консервативным.