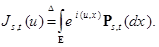|
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Из (38) следует равенство
Из (39) следует, что если положить 7.2. Пусть q - вероятностная мера на
причем Определение. МПШ Таким образом, чтобы задать процесс с независимыми приращениями достаточно знать: а) начальное распределение вероятностей q случайного вектора б) распределение вероятностей случайных векторов
Очевидно, что если заданы q и Покажем теперь, что введенное таким образом совместное распределение определяет процесс с независимыми приращениями. Действительно, пусть
Отсюда следует независимость векторов 7.3. Процессы с независимыми приращениями (СПСП) удобно изучать с помощью характеристических функций. Пусть Дата добавления: 2015-01-18 | Просмотры: 685 | Нарушение авторских прав |
 (40)
(40) , то
, то  - будет вероятностью перехода, которая обладает свойством пространственной однородности, т.е. для
- будет вероятностью перехода, которая обладает свойством пространственной однородности, т.е. для  Очевидно, что верно обратное утверждение, если переходная вероятность обладает свойством пространственной однородности, то
Очевидно, что верно обратное утверждение, если переходная вероятность обладает свойством пространственной однородности, то 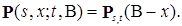
 и
и  , где
, где  - вероятностная мера на
- вероятностная мера на  , определенная формулой
, определенная формулой (41)
(41) где
где  - переходная вероятность.
- переходная вероятность. со значениями в линейном измеримом пространстве (E,E) называется процессом с независимыми приращениями, если для
со значениями в линейном измеримом пространстве (E,E) называется процессом с независимыми приращениями, если для  N
N  , tk Î R+,
, tk Î R+,  t1<t2<…<tn, случайные вектора
t1<t2<…<tn, случайные вектора  являются независимыми в совокупности, причем вектор
являются независимыми в совокупности, причем вектор  - называется начальным значением процесса
- называется начальным значением процесса  с распределением q, называемым начальным распределением.
с распределением q, называемым начальным распределением.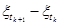
 .
.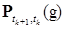 , то соотношение (41) определено совместное распределение векторов
, то соотношение (41) определено совместное распределение векторов  .
. ,где
,где  , и
, и  ,тогда имеем:
,тогда имеем: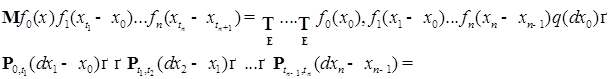
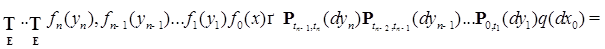
 (42)
(42) для
для  .
. и
и