 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Вероятностями перехода МПШ
2.1. Пусть
где
для любых
Следовательно
2.2. Определим, теперь, второе семейство операторов. Пусть
Стало быть, закон композиции операторов
Очевидны следующие свойства оператора 1) 2.3. Определение. МПШ называется однородным (ОМПШ), если
Поэтому удобно ввести обозначение Для ОМПШ соотношение Чепмена-Колмогорова будет иметь вид:
В этом случае семейства операторов
Очевидно, что:
Дата добавления: 2015-01-18 | Просмотры: 728 | Нарушение авторских прав |
 – множество всех конечных мер на
– множество всех конечных мер на  и
и  . Пусть
. Пусть 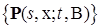 - семейство переходных вероятностей некоторого марковского процесса в широком смысле. Обозначим
- семейство переходных вероятностей некоторого марковского процесса в широком смысле. Обозначим , (5)
, (5) (6)
(6) и
и  . Ясно, что
. Ясно, что  - двухпараметрическое семейство операторов. Из соотношения Чепмена-Колмогорова следует закон композиции операторов
- двухпараметрическое семейство операторов. Из соотношения Чепмена-Колмогорова следует закон композиции операторов  . Действительно, пусть
. Действительно, пусть  , тогда в силу соотношения Чепмена-Колмогорова и теоремы Фубини, имеем:
, тогда в силу соотношения Чепмена-Колмогорова и теоремы Фубини, имеем: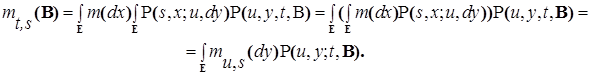
 . (7)
. (7) - множество измеримых ограниченных функций на
- множество измеримых ограниченных функций на  со значениями в
со значениями в  . Положим
. Положим  , т.е.
, т.е.  . Из определения вероятности перехода следует, что
. Из определения вероятности перехода следует, что  - измеримая по
- измеримая по  функция. Если в
функция. Если в  ввести норму
ввести норму  , то, очевидно,
, то, очевидно,  . Следовательно,
. Следовательно,  – двухпараметрическое семейство операторов. Из соотношения Чепмена-Колмогорова при
– двухпараметрическое семейство операторов. Из соотношения Чепмена-Колмогорова при  следуют равенства
следуют равенства
 имеет вид
имеет вид (8)
(8) :
: , 2)
, 2) 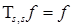 .
.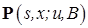 зависят только от разности
зависят только от разности  , т.е.
, т.е. (9)
(9) .
.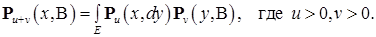
 не зависят от
не зависят от  и поэтому вместо двухпараметрического семейства операторов
и поэтому вместо двухпараметрического семейства операторов  естественно рассматривать однопараметрические семейства
естественно рассматривать однопараметрические семейства  , определенные по правилам,
, определенные по правилам,  :
: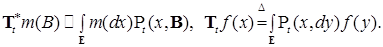
 . (10)
. (10)