 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Диффузионные процессы8.1. Определение. МПШ называется диффузионным, если выполняются условия: i) для любого ii) существуют вектор-функция
при этом Будем обозначать через 8.2. Условия i), ii) неудобны для проверки, поэтому в данном пункте мы приведем достаточные условия того, что процесс Теорема 11. Для того чтобы n -мерный МПШ i) для некоторого
ii) существуют функции
Доказательство. Проведем его для случая n =1. Действительно, в этом случае
Отсюда следует утверждение теоремы. 8.3. Теорема 12. Пусть
Доказательство. Пусть
В силу формулы Тейлора, имеем
где
Подставим (60) в (59), имеем:
где Разделим левую и правую части (61) на Покажем, теперь, в силу непрерывности функции 8.4. Предположим, что у переходной вероятности
где Теорема 13. Пусть условия (54)-(56) выполняются равномерно по x и существуют непрерывные производные
Тогда функция
Доказательство. Пусть
В силу условий теоремы и последнего равенства, имеем:
Рассмотрим теперь правую часть последнего равенства и заметим, что
Из последнего равенства, имеем
Утверждение теоремы следует из (64), в силу произвольности функции f (y).
Дата добавления: 2015-01-18 | Просмотры: 768 | Нарушение авторских прав |
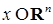 и
и  vравномерно по
vравномерно по 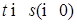
 , где
, где 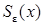 - сфера радиуса ε с центром в точке x, а
- сфера радиуса ε с центром в точке x, а 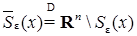 ;
;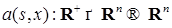 и оператор
и оператор такие, что для любых
такие, что для любых 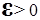 равномерно по
равномерно по 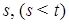
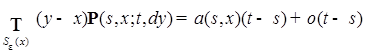 (56),
(56), (57),
(57),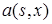 n –мерная вектор-функция называется вектором сноса, а b (s,x) матрица-функция размера
n –мерная вектор-функция называется вектором сноса, а b (s,x) матрица-функция размера 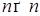 называется матрицей диффузии.
называется матрицей диффузии.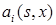 i -ую компоненту вектора сноса, а через
i -ую компоненту вектора сноса, а через 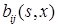
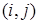 - элемент матрицы диффузии.
- элемент матрицы диффузии.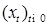 диффузионный.
диффузионный.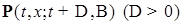 удовлетворяла условиям:
удовлетворяла условиям: , любого x равномерно по t
, любого x равномерно по t ,
,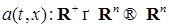 и
и 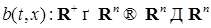 такие, что для всех t, x
такие, что для всех t, x
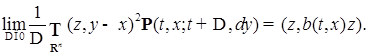
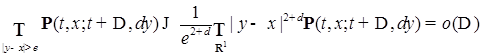 ,
,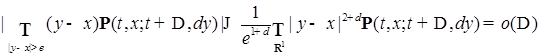 ,
,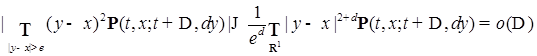 .
. -непрерывные по совокупности переменных функции. Пусть
-непрерывные по совокупности переменных функции. Пусть 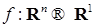 непрерывная ограниченная функция такая, что
непрерывная ограниченная функция такая, что  имеет непрерывные по совокупности переменных производные
имеет непрерывные по совокупности переменных производные 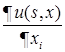 ,
, 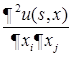 для любых
для любых  . Тогда существует производная
. Тогда существует производная  и
и 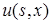 удовлетворяет уравнению:
удовлетворяет уравнению: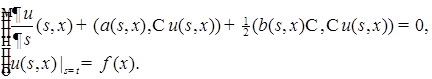 (58)
(58) . Очевидно, что
. Очевидно, что 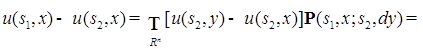
 (59)
(59) (60)
(60) ,
, 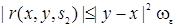
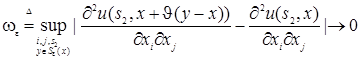 при
при 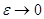 , причем
, причем 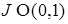 .
.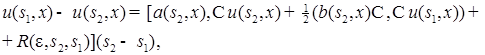 (61)
(61)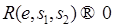 , когда
, когда 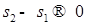 .
.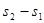 , а затем, переходя к пределу
, а затем, переходя к пределу 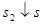 и
и 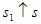 , учитывая при этом непрерывность слагаемых правой части (61) по
, учитывая при этом непрерывность слагаемых правой части (61) по 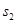 , получаем уравнение (58).
, получаем уравнение (58).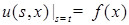 . Действительно, из равенства
. Действительно, из равенства 
 получаем требуемое равенство. Доказательство закончено.
получаем требуемое равенство. Доказательство закончено.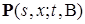 существует плотность, т.е. существует функция
существует плотность, т.е. существует функция  такая, что для
такая, что для 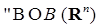
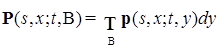 . Очевидно, что в этом случае соотношение Чепмена-Колмогорова для
. Очевидно, что в этом случае соотношение Чепмена-Колмогорова для 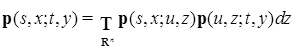 (62),
(62), . Покажем теперь, что, если плотность
. Покажем теперь, что, если плотность 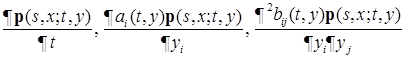 , где
, где 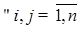 .
.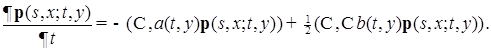 (63)
(63)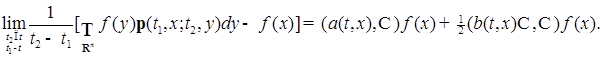
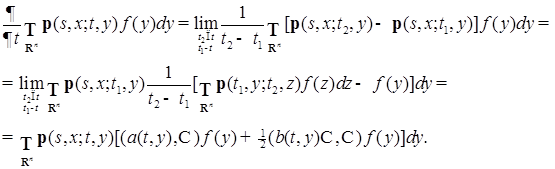
 равна нулю вне некоторого компакта, тогда в силу формулы интегрирования по частям, имеем
равна нулю вне некоторого компакта, тогда в силу формулы интегрирования по частям, имеем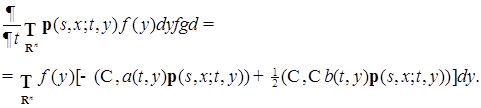
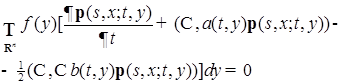 (64)
(64)