 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Классификация МПШ по свойствам траекторий
3.1. Скачкообразные МПШ - это марковский процесс, который стартует в момент времени 0 из некоторой точки пространства 3.2. Диффузионные МПШ – это марковский процесс с непрерывными траекториями. 3.3. Диффузионные процессы со скачками – это МПШ, у которого на интервалах между соседними скачками траектория представляет собой диффузионный процесс. 3.4. Процессы с независимым приращением. Пусть имеется отрезок
Дата добавления: 2015-01-18 | Просмотры: 651 | Нарушение авторских прав |
 и пребывает в нем некоторое время
и пребывает в нем некоторое время 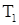 , после чего он скачком случайного размера переходит в другую точку
, после чего он скачком случайного размера переходит в другую точку 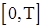 , а
, а 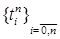 - любое разбиение отрезка
- любое разбиение отрезка  - МПШ со значениями в линейном пространстве Е. Пусть
- МПШ со значениями в линейном пространстве Е. Пусть 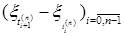 - семейство случайных элементов, независимых в совокупности для любого способа разбиения
- семейство случайных элементов, независимых в совокупности для любого способа разбиения