 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Глава 5. Марковские процессы в широком смысле. 7 страница
Глава 5. Марковские процессы в широком смысле. Введение. В основе понятия марковского случайного процесса лежит идея отсутствия последействия. Поясним это. Представим себе динамическую систему, все возможные состояния которой лежат в В этой главе мы приводим теорию случайных процессов с непрерывным временем, у которых отсутствует последействие.
§1. Переходные вероятности. Определение марковского процесса.
1.1. Пусть имеется стохастический базис Определение. Случайный процесс
для любого Замечание. В силу теоремы Бореля для каждого а) измеримый функционал Р – п.н. б) измеримая функция причем, в силу (1) Р – п.н. 1.2. Пусть Определение. Пусть 1) 2) Тогда Гипотеза H1. Существует семейство переходных вероятностей Определение. Если - Предложение 1. Пусть
где Доказательство. Доказательство утверждения предложения 1 проводится аналогично доказательству теоремы 1 гл. 2, поэтому его не приводим.
Соглашение H2: Пусть Определение. Марковским процессом в широком смысле (МПШ) называется такой процесс, что: i) принимает значения в ii) iii) выполнены гипотеза Н1 и соглашение Н2. 1.3. Закон входа МПШ. Пусть
Равенство (4) называется законом входа для МПШ.
Дата добавления: 2015-01-18 | Просмотры: 777 | Нарушение авторских прав |
 . Через
. Через 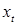 обозначим ее состояние в момент времени
обозначим ее состояние в момент времени  и предположим, что мы имеем возможность наблюдать ее состояние в любой момент времени t. Через
и предположим, что мы имеем возможность наблюдать ее состояние в любой момент времени t. Через  обозначим наблюдаемую траекторию системы до момента времени t. Через
обозначим наблюдаемую траекторию системы до момента времени t. Через  и
и  обозначим, состояние системы в момент времени
обозначим, состояние системы в момент времени 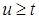 зависящее от всей ее траектории до момента времени t и от ее состояния
зависящее от всей ее траектории до момента времени t и от ее состояния 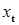 в момент времени t, соответственно. Если для любых
в момент времени t, соответственно. Если для любых  справедливо равенство
справедливо равенство  , то в этом случае говорят, что у системы отсутствует последствие.
, то в этом случае говорят, что у системы отсутствует последствие. . Пусть на стохастическом базисе задан случайный процесс
. Пусть на стохастическом базисе задан случайный процесс  со значениями в
со значениями в  , где
, где  – польское пространство. Будем считать, что
– польское пространство. Будем считать, что 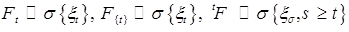
 называется марковским, если для
называется марковским, если для  , Р – п.н.
, Р – п.н. (1)
(1) .
. существуют:
существуют: , обозначаемый через
, обозначаемый через 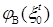 , такой, что
, такой, что  , следовательно
, следовательно 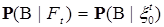
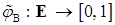 , обозначаемая через
, обозначаемая через  , такая, что
, такая, что  , следовательно
, следовательно 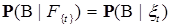 Р – п.н.
Р – п.н. , т.е.
, т.е.  Р – п.н.
Р – п.н. – измеримое пространство, Е – польское (полное сепарабельное метрическое) пространство,
– измеримое пространство, Е – польское (полное сепарабельное метрическое) пространство,  .
.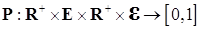 , обозначаемая
, обозначаемая 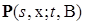 , такая, что
, такая, что 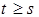 и
и - при фиксированных
- при фиксированных  – мера;
– мера;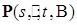 - при фиксированных
- при фиксированных 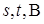 – измеримая (по Борелю) функция.
– измеримая (по Борелю) функция.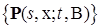 для марковского процесса
для марковского процесса  , такое, что Р – п.н. для любого
, такое, что Р – п.н. для любого 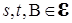
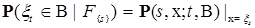 (2)
(2) и выполнено (2), то мы будем говорить, что задан марковский процесс с семейством переходных вероятностей
и выполнено (2), то мы будем говорить, что задан марковский процесс с семейством переходных вероятностей  справедливо
справедливо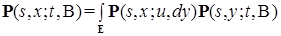 (3)
(3)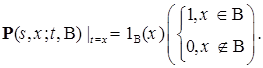
 и
и 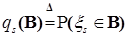 , где
, где  . (4)
. (4)