Замечание. В доказательстве теоремы 10 вместо формулы (46) удобнее воспользоваться следующей
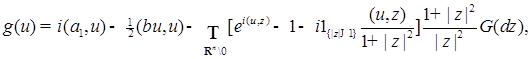 (47) (47)
где  , , 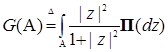
Доказательство. Пусть  – распределение вероятностей процесса – распределение вероятностей процесса  , а , а 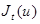 соответствующая ему характеристическая функция. Положим для соответствующая ему характеристическая функция. Положим для  B( B(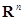 ) ) 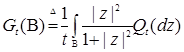 . Предположим, что семейство мер . Предположим, что семейство мер 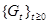 - слабо компактно. Пусть - слабо компактно. Пусть  - последовательность такая, что: a) - последовательность такая, что: a)  при при  ; б) ; б)  слабо сходится к некоторой мере слабо сходится к некоторой мере  на B( на B(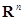 ). Тогда имеем ). Тогда имеем
 (48) (48)
где 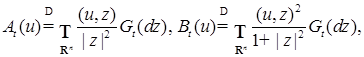
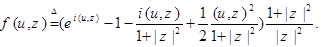
Так как  , то , то  - непрерывна и ограничена. Поэтому, в силу слабой сходимости - непрерывна и ограничена. Поэтому, в силу слабой сходимости  к к  при при  , имеем , имеем
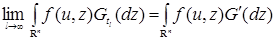 . .
Значит, при 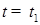 и и  существуют пределы существуют пределы 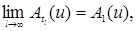  где где 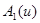 - линейная функция, т.е. - линейная функция, т.е.  , а , а  - положительно определенная квадратическая форма, т.е. - положительно определенная квадратическая форма, т.е.  , соответственно. Поэтому в (48) можно произвести предельный переход при , соответственно. Поэтому в (48) можно произвести предельный переход при 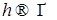 , получим , получим
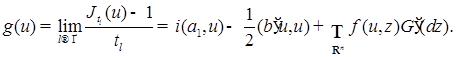
Пусть 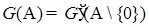 , где {0} - одноточечное множество, “состоящее” из точки “нуль”. Так как , где {0} - одноточечное множество, “состоящее” из точки “нуль”. Так как  , то , то 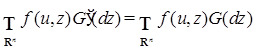 . Кроме того, интеграл . Кроме того, интеграл  существует и представляет собой положительно определенную квадратическую форму по u, т.е. существует и представляет собой положительно определенную квадратическую форму по u, т.е.  . Из приведенных построений следует, что . Из приведенных построений следует, что 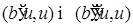 . Поэтому существует положительно определенная матрица . Поэтому существует положительно определенная матрица  , такая что , такая что  , ,
что и доказывает (47).
Установим слабую компактность семейства мер  . В силу теоремы 36 главы 1 нужно установить, что: а) . В силу теоремы 36 главы 1 нужно установить, что: а)  ; б) ; б)  где где  . .
Пусть  , ,  . В силу условий теоремы и (46), получаем, что для любого . В силу условий теоремы и (46), получаем, что для любого  существует такое существует такое  , что , что
 , при , при  (49) (49)
и при 
 , при , при  . (50) . (50)
Так как  для для  , то из (49) следует, что , то из (49) следует, что
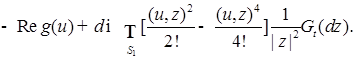 (51) (51)
Нам понадобятся значения интегралов:
 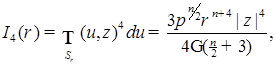
где Г(k) - Гамма-функция, 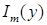 - функция Бесселя, порядка m действительного аргумента. Проинтегрируем неравенства (49), (50) по - функция Бесселя, порядка m действительного аргумента. Проинтегрируем неравенства (49), (50) по 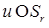 , а затем получившийся результат разделим на , а затем получившийся результат разделим на  , ( , ( ), имеем: ), имеем:
 (52) (52)
 (53) (53)
Рассмотрим (52), пусть  и и 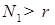 , имеем , имеем
 . .
Рассмотрим (53). Так как  - ограничена, то можно выбрать (при любом c >0) - ограничена, то можно выбрать (при любом c >0)  таким, что таким, что
 (54) (54)
Тогда имеем  . .
Из вышеприведенных рассуждений следует, что  , для любого t. , для любого t.
Заметим, что  . Выберем теперь . Выберем теперь 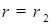 таким, что левая часть (52) не превосходила таким, что левая часть (52) не превосходила  , а , а  cтаким, чтобы выполнялось (54). Тогда получаем, что cтаким, чтобы выполнялось (54). Тогда получаем, что 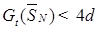 для любого t. Доказательство закончено. для любого t. Доказательство закончено.
7.6. Рассмотрим частные случаи формулы (47), когда n =1.
1) Пусть 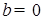 и и  для любого для любого 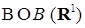 . В этом случае . В этом случае  . Это соответствует характеристической функции вырожденного распределения, сосредоточенного в точке . Это соответствует характеристической функции вырожденного распределения, сосредоточенного в точке 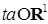 . Следовательно, . Следовательно,  , т.е. точка , т.е. точка 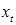 движется с постоянной скоростью а. движется с постоянной скоростью а.
2) Пусть  для любого для любого 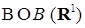 . В этом случае приращения . В этом случае приращения  имеют нормальное распределение со средним имеют нормальное распределение со средним  и дисперсией равной и дисперсией равной  . Если . Если  , то процесс , то процесс 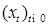 является гауссовским. Отметим, что если является гауссовским. Отметим, что если  и и  , то такой процесс называется винеровским. , то такой процесс называется винеровским.
3) Пусть  и и 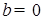 , а мера П сосредоточена в точке {1} и имеет в ней массу, равную единице. Тогда характеристическая функция будет иметь вид , а мера П сосредоточена в точке {1} и имеет в ней массу, равную единице. Тогда характеристическая функция будет иметь вид  . Отсюда следует, что . Отсюда следует, что  . Этот процесс называется стандартным пуассоновским, который был подробно рассмотрен нами в главе 3. . Этот процесс называется стандартным пуассоновским, который был подробно рассмотрен нами в главе 3.
Дата добавления: 2015-01-18 | Просмотры: 789 | Нарушение авторских прав
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
|

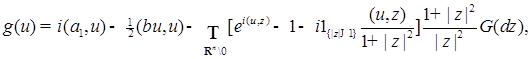 (47)
(47) ,
, 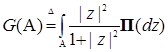
 – распределение вероятностей процесса
– распределение вероятностей процесса  , а
, а 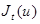 соответствующая ему характеристическая функция. Положим для
соответствующая ему характеристическая функция. Положим для 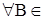 B(
B(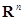 )
) 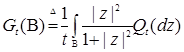 . Предположим, что семейство мер
. Предположим, что семейство мер 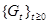 - слабо компактно. Пусть
- слабо компактно. Пусть  - последовательность такая, что: a)
- последовательность такая, что: a)  при
при  ; б)
; б)  слабо сходится к некоторой мере
слабо сходится к некоторой мере  на B(
на B( (48)
(48)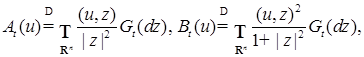
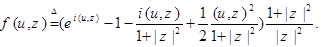
 , то
, то  - непрерывна и ограничена. Поэтому, в силу слабой сходимости
- непрерывна и ограничена. Поэтому, в силу слабой сходимости  к
к 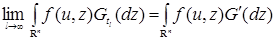 .
.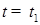 и
и 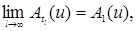
 где
где 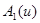 - линейная функция, т.е.
- линейная функция, т.е.  , а
, а  - положительно определенная квадратическая форма, т.е.
- положительно определенная квадратическая форма, т.е.  , соответственно. Поэтому в (48) можно произвести предельный переход при
, соответственно. Поэтому в (48) можно произвести предельный переход при 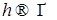 , получим
, получим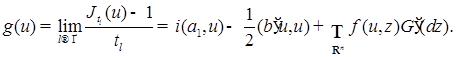
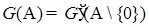 , где {0} - одноточечное множество, “состоящее” из точки “нуль”. Так как
, где {0} - одноточечное множество, “состоящее” из точки “нуль”. Так как  , то
, то 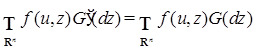 . Кроме того, интеграл
. Кроме того, интеграл  существует и представляет собой положительно определенную квадратическую форму по u, т.е.
существует и представляет собой положительно определенную квадратическую форму по u, т.е.  . Из приведенных построений следует, что
. Из приведенных построений следует, что 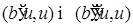 . Поэтому существует положительно определенная матрица
. Поэтому существует положительно определенная матрица  , такая что
, такая что  ,
, . В силу теоремы 36 главы 1 нужно установить, что: а)
. В силу теоремы 36 главы 1 нужно установить, что: а)  ; б)
; б)  где
где  .
. ,
,  . В силу условий теоремы и (46), получаем, что для любого
. В силу условий теоремы и (46), получаем, что для любого  существует такое
существует такое  , что
, что , при
, при  (49)
(49)
 , при
, при  . (50)
. (50) для
для  , то из (49) следует, что
, то из (49) следует, что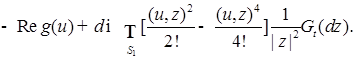 (51)
(51)
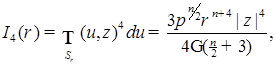
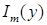 - функция Бесселя, порядка m действительного аргумента. Проинтегрируем неравенства (49), (50) по
- функция Бесселя, порядка m действительного аргумента. Проинтегрируем неравенства (49), (50) по  , а затем получившийся результат разделим на
, а затем получившийся результат разделим на  , (
, ( ), имеем:
), имеем: (52)
(52) (53)
(53) и
и  , имеем
, имеем .
. - ограничена, то можно выбрать (при любом c >0)
- ограничена, то можно выбрать (при любом c >0)  таким, что
таким, что (54)
(54) .
. , для любого t.
, для любого t. . Выберем теперь
. Выберем теперь 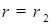 таким, что левая часть (52) не превосходила
таким, что левая часть (52) не превосходила  , а
, а  cтаким, чтобы выполнялось (54). Тогда получаем, что
cтаким, чтобы выполнялось (54). Тогда получаем, что 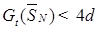 для любого t. Доказательство закончено.
для любого t. Доказательство закончено.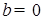 и
и  для любого
для любого 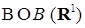 . В этом случае
. В этом случае  . Это соответствует характеристической функции вырожденного распределения, сосредоточенного в точке
. Это соответствует характеристической функции вырожденного распределения, сосредоточенного в точке 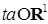 . Следовательно,
. Следовательно,  , т.е. точка
, т.е. точка 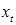 движется с постоянной скоростью а.
движется с постоянной скоростью а. имеют нормальное распределение со средним
имеют нормальное распределение со средним  и дисперсией равной
и дисперсией равной  . Если
. Если  , то процесс
, то процесс 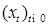 является гауссовским. Отметим, что если
является гауссовским. Отметим, что если  и
и  , то такой процесс называется винеровским.
, то такой процесс называется винеровским. и
и  . Отсюда следует, что
. Отсюда следует, что  . Этот процесс называется стандартным пуассоновским, который был подробно рассмотрен нами в главе 3.
. Этот процесс называется стандартным пуассоновским, который был подробно рассмотрен нами в главе 3.