Матрица интенсивности перехода. Уравнения Колмогорова
10.1. Пусть на стохастическом базисе  задан опциональный процесс задан опциональный процесс  со значениями в Е, где Е – конечное или счетное множество. Пусть со значениями в Е, где Е – конечное или счетное множество. Пусть  – последовательность марковских моментов, которая исчерпывает все скачки процесса – последовательность марковских моментов, которая исчерпывает все скачки процесса  . Без ограничения общности можно считать, что . Без ограничения общности можно считать, что  . Пусть . Пусть   - считающий процесс, а - считающий процесс, а 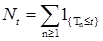 , относительно которых мы будем предполагать, что выполняются условия (N): , относительно которых мы будем предполагать, что выполняются условия (N):
i) 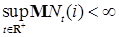 для любого для любого 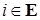 ; ;
ii)  . .
Если выполнено условие  ,то у считающего процесса ,то у считающего процесса 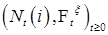 существует существует  - компенсатор - компенсатор  , относительно которого мы будем полагать, что выполняется условие (А): , относительно которого мы будем полагать, что выполняется условие (А):
P – п. н. для любых   , причем , причем
 измерима, где измерима, где 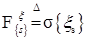 . .
10.2. Предложение 34. Пусть  опциональный случайный процесс с конечным или счетным множеством состояний E, а опциональный случайный процесс с конечным или счетным множеством состояний E, а  -считающий процесс. Пусть выполняются условия (N), (А). Тогда существует измеримая функция -считающий процесс. Пусть выполняются условия (N), (А). Тогда существует измеримая функция  , обозначаемая , обозначаемая  такая, что: такая, что:
1) почти всюду относительно меры Лебега:
i)  для любых для любых 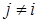 , ,
ii)  для любых для любых 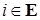 ; ;
2) компенсатор считающего процесса 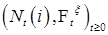 имеет вид имеет вид  ; ;
3) компенсатор процесса  имеет вид имеет вид  . .
Доказательство. 1) Рассмотрим считающий процесс 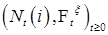 , , 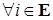 . В силу пункта 2) предложения 33 и теоремы Блекуэлла для любой . В силу пункта 2) предложения 33 и теоремы Блекуэлла для любой  предсказуемой ограниченной неотрицательной функции предсказуемой ограниченной неотрицательной функции  справедливо равенство: справедливо равенство:

 . (7) . (7)
Из условия (А) следует, что  - измерима, поэтому в силу теоремы Бореля, существует измеримая функция - измерима, поэтому в силу теоремы Бореля, существует измеримая функция  , обозначаемая через , обозначаемая через 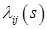 , такая, что , такая, что  почти всюду относительно меры почти всюду относительно меры  . Очевидно, что . Очевидно, что  . Поэтому (7) можно переписать в виде . Поэтому (7) можно переписать в виде 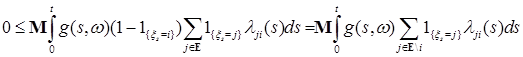 . .
Из последнего равенства, в силу произвольности функции  получаем, что: получаем, что:
1)  для для  почти всех s, 2) почти всех s, 2)  -компенсатор считающего процесса -компенсатор считающего процесса 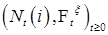 . Таким образом, второе утверждение предложения установлено. . Таким образом, второе утверждение предложения установлено.
3) Рассмотрим процесс  . Из определения процесса . Из определения процесса  и условий предложения для любой и условий предложения для любой  - предсказуемой ограниченной неотрицательной функции - предсказуемой ограниченной неотрицательной функции  определен и конечен интеграл определен и конечен интеграл  для любого для любого  . В силу условий предположения и свойств интеграла Стилтьеса, имеем . В силу условий предположения и свойств интеграла Стилтьеса, имеем
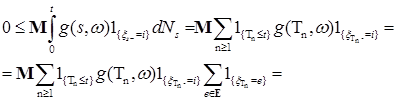
 (8) (8)
Ранее мы выяснили, что  - компенсатор считающего процесса - компенсатор считающего процесса  имеет вид имеет вид  . Поэтому для любых t,i из (8) имеем . Поэтому для любых t,i из (8) имеем
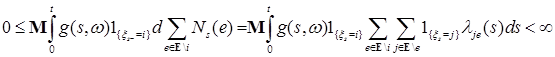
Следовательно, в силу произвольности функции  , получаем , получаем  для любых для любых 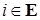 и почти всех s. Отсюда, в силу теоремы Блекуэлла и произвольности и почти всех s. Отсюда, в силу теоремы Блекуэлла и произвольности  , получаем, что предсказуемый процесс , получаем, что предсказуемый процесс  является компенсатором процесса является компенсатором процесса  . Доказательство закончено. . Доказательство закончено.
Из предложения 34 следует определение.
Определение. Измеримую функцию  , обозначаемую через , обозначаемую через  , где , где  , назовем матрицей интенсивности перехода опционального процесса , назовем матрицей интенсивности перехода опционального процесса  с конечным или счетным числом состояний, если выполняются условия: с конечным или счетным числом состояний, если выполняются условия:
1) для почти всех s
i)  для любых для любых 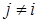 , ,
ii)  для любого для любого 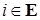 , ,
iii)  . .
2) относительно потока  и меры P процессы и и меры P процессы и 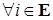 : :
i)  , ,
ii) 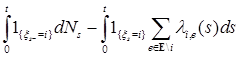
являются мартингалами.
Теорема 35. Пусть выполнены условия (N), (А). Тогда справедливы следующие утверждения:
1) существует матрица интенсивности перехода у опционального процесса  с конечным или счетным числом состояний; с конечным или счетным числом состояний;
2) пусть  - матрица интенсивности перехода опционального процесса - матрица интенсивности перехода опционального процесса  с конечным или счетным числом состояний. Тогда Р – п.н. справедливо представление для любых с конечным или счетным числом состояний. Тогда Р – п.н. справедливо представление для любых  и и 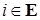 . .
 . (9) . (9)
где  - мартингал. - мартингал.
Доказательство. Первое утверждение следует из предложения 34. Второе утверждение теоремы следует из предложений 33 и 34.
Действительно, из пункта 1) предложения 33 и пункта 3 предложения 34, имеем P – п.н.
 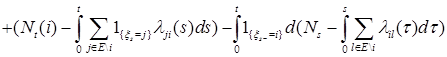
Здесь мы учли, что  . Для завершения доказательства осталось лишь заметить, что в силу пунктов 2) и 3) предложения 34 . Для завершения доказательства осталось лишь заметить, что в силу пунктов 2) и 3) предложения 34  и и  являются мартингалами относительно меры P. Доказательство закончено. являются мартингалами относительно меры P. Доказательство закончено.
Замечание. Предположим, что  - матрица интенсивности перехода удовлетворяет условиям: - матрица интенсивности перехода удовлетворяет условиям:
1)  для для  и и  , ,
2)  , ,
3)  . .
Тогда  . Действительно, из условий 1) – 3) следует, что для . Действительно, из условий 1) – 3) следует, что для   . .
10.3. Представление (9) позволяет вывести уравнение для распределения вероятностей  . Обозначим . Обозначим  . .
Теорема 36. Пусть  - матрица интенсивностей перехода процесса - матрица интенсивностей перехода процесса  . Тогда . Тогда  удовлетворяет системе уравнений для удовлетворяет системе уравнений для 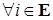
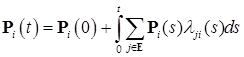 . (10) . (10)
Доказательство. Возьмем математическое ожидание относительно левой и правой частей (9), учитывая, что  для для  , имеем , имеем
 . .
Так как  для для  , то в силу теоремы Фубини из последнего равенства имеем , то в силу теоремы Фубини из последнего равенства имеем
 . .
Отсюда, в силу того, что  детерминированная функция, получаем (10). Доказательство закончено. детерминированная функция, получаем (10). Доказательство закончено.
Замечание. Процесс  , распределение вероятностей которого удовлетворяет (10) называют скачкообразным марковским процессом с конечным или счетным числом состояний. Система уравнений (10) называется прямым уравнением Колмогорова для марковских процессов с конечным или счетным числом состояний. , распределение вероятностей которого удовлетворяет (10) называют скачкообразным марковским процессом с конечным или счетным числом состояний. Система уравнений (10) называется прямым уравнением Колмогорова для марковских процессов с конечным или счетным числом состояний.
Дата добавления: 2015-01-18 | Просмотры: 1318 | Нарушение авторских прав
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|

 задан опциональный процесс
задан опциональный процесс  со значениями в Е, где Е – конечное или счетное множество. Пусть
со значениями в Е, где Е – конечное или счетное множество. Пусть  – последовательность марковских моментов, которая исчерпывает все скачки процесса
– последовательность марковских моментов, которая исчерпывает все скачки процесса  . Пусть
. Пусть 
 - считающий процесс, а
- считающий процесс, а 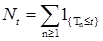 , относительно которых мы будем предполагать, что выполняются условия (N):
, относительно которых мы будем предполагать, что выполняются условия (N):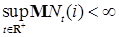 для любого
для любого 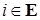 ;
; .
. ,то у считающего процесса
,то у считающего процесса 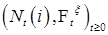 существует
существует  - компенсатор
- компенсатор  , относительно которого мы будем полагать, что выполняется условие (А):
, относительно которого мы будем полагать, что выполняется условие (А):
 , причем
, причем измерима, где
измерима, где 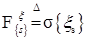 .
. -считающий процесс. Пусть выполняются условия (N), (А). Тогда существует измеримая функция
-считающий процесс. Пусть выполняются условия (N), (А). Тогда существует измеримая функция  , обозначаемая
, обозначаемая  такая, что:
такая, что: для любых
для любых 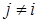 ,
, для любых
для любых  ;
; имеет вид
имеет вид  .
.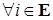 . В силу пункта 2) предложения 33 и теоремы Блекуэлла для любой
. В силу пункта 2) предложения 33 и теоремы Блекуэлла для любой  справедливо равенство:
справедливо равенство:
 . (7)
. (7) - измерима, поэтому в силу теоремы Бореля, существует измеримая функция
- измерима, поэтому в силу теоремы Бореля, существует измеримая функция 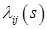 , такая, что
, такая, что  почти всюду относительно меры
почти всюду относительно меры  . Очевидно, что
. Очевидно, что  . Поэтому (7) можно переписать в виде
. Поэтому (7) можно переписать в виде 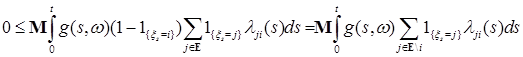 .
. для
для  почти всех s, 2)
почти всех s, 2)  -компенсатор считающего процесса
-компенсатор считающего процесса  и условий предложения для любой
и условий предложения для любой  определен и конечен интеграл
определен и конечен интеграл  для любого
для любого  . В силу условий предположения и свойств интеграла Стилтьеса, имеем
. В силу условий предположения и свойств интеграла Стилтьеса, имеем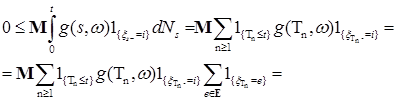
 (8)
(8) имеет вид
имеет вид  . Поэтому для любых t,i из (8) имеем
. Поэтому для любых t,i из (8) имеем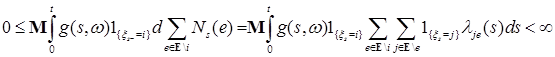
 для любых
для любых  . Доказательство закончено.
. Доказательство закончено. , назовем матрицей интенсивности перехода опционального процесса
, назовем матрицей интенсивности перехода опционального процесса  с конечным или счетным числом состояний, если выполняются условия:
с конечным или счетным числом состояний, если выполняются условия: для любого
для любого  .
. ,
,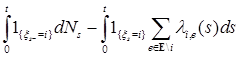
 - матрица интенсивности перехода опционального процесса
- матрица интенсивности перехода опционального процесса  и
и  . (9)
. (9) - мартингал.
- мартингал.
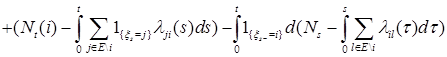
 . Для завершения доказательства осталось лишь заметить, что в силу пунктов 2) и 3) предложения 34
. Для завершения доказательства осталось лишь заметить, что в силу пунктов 2) и 3) предложения 34  и
и  являются мартингалами относительно меры P. Доказательство закончено.
являются мартингалами относительно меры P. Доказательство закончено. - матрица интенсивности перехода удовлетворяет условиям:
- матрица интенсивности перехода удовлетворяет условиям: для
для  и
и  ,
, .
. . Действительно, из условий 1) – 3) следует, что для
. Действительно, из условий 1) – 3) следует, что для 
 .
. . Обозначим
. Обозначим  .
. - матрица интенсивностей перехода процесса
- матрица интенсивностей перехода процесса  . Тогда
. Тогда  удовлетворяет системе уравнений для
удовлетворяет системе уравнений для 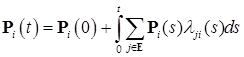 . (10)
. (10) для
для  , имеем
, имеем .
. для
для  , то в силу теоремы Фубини из последнего равенства имеем
, то в силу теоремы Фубини из последнего равенства имеем .
. детерминированная функция, получаем (10). Доказательство закончено.
детерминированная функция, получаем (10). Доказательство закончено.