 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Заметим, что
Поэтому
Продолжая этот процесс далее, получаем, что P – п.н.
который является решением этого уравнения. Легко показать, что 1) а) Р - п. н. в) 2) а) Р - п. н. Р - п. н. 3) а) в) для Таким образом, доказано утверждение. Теорема 49. Пусть выполнены условия 1), 3). Тогда уравнение (17) имеет единственное положительное решение, которое имеет вид (19), причем если выполнено условие 2), то Р - п. н. Замечание. Из теоремы 49 следует, что с помощью процесса 15.4. Теорема 50 (Гирсанов). Пусть Доказательство. Пусть
Дата добавления: 2015-01-18 | Просмотры: 687 | Нарушение авторских прав |
 .
. ×
× .
.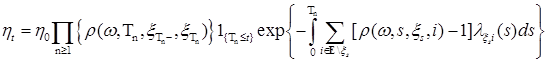 ,(20)
,(20) если выполняются условия:
если выполняются условия: , б) для
, б) для  Р - п. н.,
Р - п. н., для
для 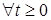 Р - п. н.;
Р - п. н.; если выполняются условия:
если выполняются условия: , б) для
, б) для  Р -п. н., в) для
Р -п. н., в) для 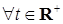
 ;
; если выполняются условия:
если выполняются условия: Р - п. н., б) для
Р - п. н., б) для  Р - п. н.,
Р - п. н., .
. для
для 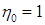 , то для
, то для  и является равномерно интегрируемым мартингалом (относительно меры Р).
и является равномерно интегрируемым мартингалом (относительно меры Р). , где
, где  . Очевидно,
. Очевидно,  , а
, а  - производная Радона – Никодима меры Q относительно меры P.
- производная Радона – Никодима меры Q относительно меры P. опциональный случайный процесс с конечным или счетным множеством состояний Е и матрицей интенсивности перехода
опциональный случайный процесс с конечным или счетным множеством состояний Е и матрицей интенсивности перехода  . Пусть
. Пусть  удовлетворяет условиями 1)-3) теоремы 44. Тогда относительно меры
удовлетворяет условиями 1)-3) теоремы 44. Тогда относительно меры  , где
, где  .
. - целочисленная случайная мера, построенная по скачкам процесса
- целочисленная случайная мера, построенная по скачкам процесса  , т. е.
, т. е.  является мартингалом относительно меры Р. Нам надо показать, что относительно меры Q процесс
является мартингалом относительно меры Р. Нам надо показать, что относительно меры Q процесс 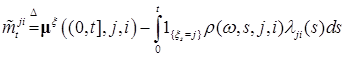 - мартингал относительно потока
- мартингал относительно потока  , т. е. Q - п. н.
, т. е. Q - п. н.  . Последнее равенство выполнено тогда и только тогда, когда
. Последнее равенство выполнено тогда и только тогда, когда  для
для 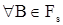 . Из определения меры Q следует
. Из определения меры Q следует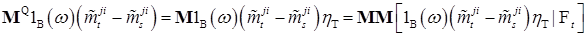 .
.