Марковские моменты
3.1. Определение. Пусть  - случайная величина - случайная величина  называется марковским моментом, если называется марковским моментом, если 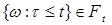 для для  . .
Конечный марковский момент называется моментом остановки (т. е.  ). ).
Пример. Пусть  непрерывен справа со значениями в непрерывен справа со значениями в 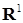 тогда момент первого достижения уровня тогда момент первого достижения уровня  : : 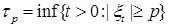 , является марковским моментом. , является марковским моментом.
Теорема 10. 1) Пусть  - марковский момент, тогда - марковский момент, тогда 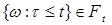
2) Пусть  - марковский момент, тогда - марковский момент, тогда  . .
Доказательство. 1) Так как  - марковский момент, то - марковский момент, то  . Отсюда при . Отсюда при 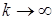 получаем получаем  . .
2) Так как  , то из пункта 1) получаем утверждение. Доказательство закончено. , то из пункта 1) получаем утверждение. Доказательство закончено.
Теорема 11. Если  и и  - марковские моменты, то: 1) - марковские моменты, то: 1) 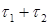 - марковский момент, 2) - марковский момент, 2)  - марковский момент. - марковский момент.
Докажите самостоятельно.
3.2. Возникает естественный вопрос: при каких условиях случайная величина  является марковским моментом? является марковским моментом?
Теорема 12. Случайная величина  - марковский момент, если - марковский момент, если  для для 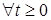 . .
Доказательство. Так как  - случайная величина, то - случайная величина, то  . Докажем, что . Докажем, что 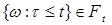 . Из определения случайной величины следует, что . Из определения случайной величины следует, что  Пересечем все эти множества, имеем Пересечем все эти множества, имеем  , для , для  . Поэтому в силу условий теоремы имеем . Поэтому в силу условий теоремы имеем  .Доказательство закончено. .Доказательство закончено.
Теорема 13. Если есть два марковских момента, то  и и  - марковские моменты. - марковские моменты.
Докажите самостоятельно.
3.3. Определение. Пусть  — марковские моменты (м. м.), причём — марковские моменты (м. м.), причём  Р - п. н.. Множества Р - п. н.. Множества

называются, соответственно, открытым справа, открытым слева, открытым справа и слева, замкнутым стохастическими интервалами и обозначаются, соответственно, через 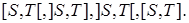
Через  обозначим множество обозначим множество  и назовём его графиком марковского момента и назовём его графиком марковского момента  . .
Задача. Докажите, что  . .
3.4. Определение. Случайное множество А называется тонким, если оно имеет вид  , где , где  - последовательность моментов остановки. Если, кроме того, последовательность - последовательность моментов остановки. Если, кроме того, последовательность  такая, что такая, что  при при  , то такую последовательность назовём исчерпывающей множество A. , то такую последовательность назовём исчерпывающей множество A.
Теорема 14. Тонкое множество А и все его  сечения сечения  не более чем счётны, кроме того, существует исчерпывающая последовательность моментов остановки. не более чем счётны, кроме того, существует исчерпывающая последовательность моментов остановки.
3.5. Определение. Случайный процесс  называется остановленным если называется остановленным если 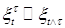 . .
Определение. Пусть последовательность марковских моментов такая, что  , причём , причём  Р -п. н. для Р -п. н. для  и пусть и пусть
 Р - п. н.. Такую последовательность назовём Р - п. н.. Такую последовательность назовём  локализующей ( локализующей (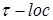 ).Если же ).Если же  , то последовательность , то последовательность  назовём локализующей. назовём локализующей.
Определение. Случайный процесс 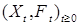 называется называется  локальным мартингалом, если существует локальным мартингалом, если существует  локализующая последовательность локализующая последовательность  марковских моментов такая, что для марковских моментов такая, что для  Р - п. н. Р - п. н.  . .
Аналогичным образом определяются локальные субмартингал и супермартингал.
Теорема 15. Пусть 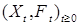 - локальный мартингал относительно меры Р. Тогда - локальный мартингал относительно меры Р. Тогда 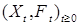 - супермартингал (относительно меры Р). - супермартингал (относительно меры Р).
Доказательство. Так как  Р — п.н. для Р — п.н. для  , где , где  - локализующая последовательность, то в силу леммы Фату - локализующая последовательность, то в силу леммы Фату  . .
Доказательство закончено.
3.6. Займемся теперь классификацией марковских моментов.
3.6.1. Определение. Марковский момент  называется предсказуемым, если существует последовательность марковских моментов называется предсказуемым, если существует последовательность марковских моментов  такая, что: а) такая, что: а) 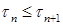 Р - п. н., б) Р - п. н., б)  Р - п. н., при этом последовательность Р - п. н., при этом последовательность  называют предвещающей марковский момент называют предвещающей марковский момент  . .
Пример. Пусть  момент остановки, а момент остановки, а  . Ясно, что . Ясно, что  момент остановки, более того момент остановки, более того  предсказуемый момент остановки, так как предсказуемый момент остановки, так как  предвещает последовательность предвещает последовательность  , где , где 
Определение. Марковский момент  называют достижимым, если существует предсказуемая последовательность называют достижимым, если существует предсказуемая последовательность  марковских моментов таких, что марковских моментов таких, что  Р - п. н., т. е. Р - п. н., т. е. 
3.6.2. Определение. Марковский момент называется недостижимым (вполне или тотально недостижимым) или опциональным, если для каждого предсказуемого момента остановки  Р - п. н.. Р - п. н..
Задача. Докажите, что если  марковский момент одновременно достижим и тотально не достижим, то марковский момент одновременно достижим и тотально не достижим, то  Р - п. н.. Р - п. н..
Теорема 16. Марковский момент  - опционален тогда и только тогда, когда существует последовательность моментов остановки - опционален тогда и только тогда, когда существует последовательность моментов остановки  такая, что: а) такая, что: а)  Р - п. н. для Р - п. н. для  , б) , б)  Р - п. н.. Р - п. н..
Докажите самостоятельно.
Очевидно следующее утверждение.
Теорема 17. Пусть  — опциональный марковский момент. Тогда для любой предсказуемой последовательности марковских моментов — опциональный марковский момент. Тогда для любой предсказуемой последовательности марковских моментов  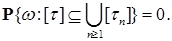
Задача. Докажите, что момент времени в который происходит первый скачок пуассоновского процесса  является опциональным марковским моментом. является опциональным марковским моментом.
Теорема 18. Пусть  где где  , и стохастические интервал вида , и стохастические интервал вида  , где , где  - опциональные марковские моменты, порождают - опциональные марковские моменты, порождают  алгебру алгебру  . .
Доказательство. Сначала заметим, что  - это предсказуемый момент остановки равный нулю на - это предсказуемый момент остановки равный нулю на  и бесконечности на и бесконечности на  . Значит . Значит  . Очевидно, что . Очевидно, что  . Заметим, что . Заметим, что  предсказуемым м. о., поэтому предсказуемым м. о., поэтому  , следовательно , следовательно  . .
Рассмотрим интервал  , где , где  - предсказуемый м.о. Нам надо показать, что этот интервал принадлежит - предсказуемый м.о. Нам надо показать, что этот интервал принадлежит  алгебре порождённой выше рассмотренными интервалами. Действительно, поскольку алгебре порождённой выше рассмотренными интервалами. Действительно, поскольку  , а для последовательностей , а для последовательностей  , предвещающей , предвещающей  на множестве на множестве  , имеем , имеем  Отсюда следует утверждение теоремы. Отсюда следует утверждение теоремы.
Дата добавления: 2015-01-18 | Просмотры: 1334 | Нарушение авторских прав
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|

 - случайная величина
- случайная величина  называется марковским моментом, если
называется марковским моментом, если 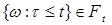 для
для  .
. ).
). непрерывен справа со значениями в
непрерывен справа со значениями в 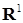 тогда момент первого достижения уровня
тогда момент первого достижения уровня  :
: 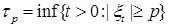 , является марковским моментом.
, является марковским моментом. .
. . Отсюда при
. Отсюда при 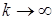 получаем
получаем  .
. , то из пункта 1) получаем утверждение. Доказательство закончено.
, то из пункта 1) получаем утверждение. Доказательство закончено. и
и  - марковские моменты, то: 1)
- марковские моменты, то: 1) 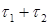 - марковский момент, 2)
- марковский момент, 2)  - марковский момент.
- марковский момент. является марковским моментом?
является марковским моментом? для
для 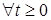 .
. . Докажем, что
. Докажем, что  Пересечем все эти множества, имеем
Пересечем все эти множества, имеем  , для
, для  . Поэтому в силу условий теоремы имеем
. Поэтому в силу условий теоремы имеем  .Доказательство закончено.
.Доказательство закончено. и
и  - марковские моменты.
- марковские моменты. — марковские моменты (м. м.), причём
— марковские моменты (м. м.), причём  Р - п. н.. Множества
Р - п. н.. Множества 
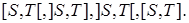
 обозначим множество
обозначим множество  и назовём его графиком марковского момента
и назовём его графиком марковского момента  .
. .
. , где
, где  - последовательность моментов остановки. Если, кроме того, последовательность
- последовательность моментов остановки. Если, кроме того, последовательность  при
при  , то такую последовательность назовём исчерпывающей множество A.
, то такую последовательность назовём исчерпывающей множество A. сечения
сечения  не более чем счётны, кроме того, существует исчерпывающая последовательность моментов остановки.
не более чем счётны, кроме того, существует исчерпывающая последовательность моментов остановки. называется остановленным если
называется остановленным если 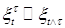 .
. Р -п. н. для
Р -п. н. для  и пусть
и пусть  Р - п. н.. Такую последовательность назовём
Р - п. н.. Такую последовательность назовём  локализующей (
локализующей (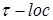 ).Если же
).Если же  , то последовательность
, то последовательность 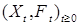 называется
называется  Р - п. н.
Р - п. н.  .
. .
.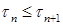 Р - п. н., б)
Р - п. н., б)  Р - п. н., при этом последовательность
Р - п. н., при этом последовательность  момент остановки, а
момент остановки, а  . Ясно, что
. Ясно, что  момент остановки, более того
момент остановки, более того  предвещает последовательность
предвещает последовательность  , где
, где 
 Р - п. н., т. е.
Р - п. н., т. е. 
 Р - п. н..
Р - п. н.. Р - п. н..
Р - п. н.. Р - п. н. для
Р - п. н. для  Р - п. н..
Р - п. н..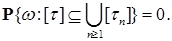
 является опциональным марковским моментом.
является опциональным марковским моментом. где
где  , и стохастические интервал вида
, и стохастические интервал вида  , где
, где  алгебру
алгебру  .
. - это предсказуемый момент остановки равный нулю на
- это предсказуемый момент остановки равный нулю на  и бесконечности на
и бесконечности на  . Значит
. Значит  . Очевидно, что
. Очевидно, что  . Заметим, что
. Заметим, что  предсказуемым м. о., поэтому
предсказуемым м. о., поэтому  , следовательно
, следовательно  .
. , где
, где  - предсказуемый м.о. Нам надо показать, что этот интервал принадлежит
- предсказуемый м.о. Нам надо показать, что этот интервал принадлежит  , а для последовательностей
, а для последовательностей  , предвещающей
, предвещающей  на множестве
на множестве  , имеем
, имеем  Отсюда следует утверждение теоремы.
Отсюда следует утверждение теоремы.