Классификация потоков s-алгебр
4.1. Пусть имеется стохастический базис 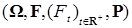 . .
Определение. Опциональной (предсказуемой)  алгеброй, обозначается через алгеброй, обозначается через  называется называется  алгебра, порождаемая стохастическими интервалами вида алгебра, порождаемая стохастическими интервалами вида  где где  — опциональный (предсказуемый) момент остановки. — опциональный (предсказуемый) момент остановки.
Из определения следует следующее утверждение.
Теорема 19. 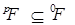 . .
4.2. Определение. Случайный процесс  со значениями в со значениями в  называется опциональным (предсказуемым), если отображение называется опциональным (предсказуемым), если отображение 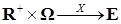 измеримо относительно измеримо относительно   алгебры на алгебры на  . .
Теорема 20. Предсказуемая  алгебра алгебра 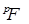 порождена всеми непрерывными слева согласованными процессами. порождена всеми непрерывными слева согласованными процессами.
Доказательство. Из теоремы 18 следует, что 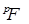 порождена всеми процессами вида порождена всеми процессами вида  , где , где 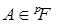 и и  , где , где  — любые опциональные марковские моменты, причём Р - п. н. — любые опциональные марковские моменты, причём Р - п. н.  . Ясно, что эти процессы непрерывны слева и согласованы. Поэтому для доказательства теоремы достаточно доказать, что каждый непрерывный слева согласованный процесс . Ясно, что эти процессы непрерывны слева и согласованы. Поэтому для доказательства теоремы достаточно доказать, что каждый непрерывный слева согласованный процесс  является предсказуемым. Обозначим является предсказуемым. Обозначим 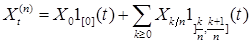 . Процесс . Процесс  - предсказуем и непрерывен слева и поэтому - предсказуем и непрерывен слева и поэтому 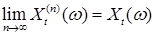 Р - п. н. Значит Р - п. н. Значит  - предсказуемый процесс. Доказательство закончено. - предсказуемый процесс. Доказательство закончено.
Теорема 21. Опциональная  алгебра порождена всеми согласованными процессами, непрерывными справа и имеющими предел слева. алгебра порождена всеми согласованными процессами, непрерывными справа и имеющими предел слева.
Доказательство. Опциональная  алгебра алгебра  порождена процессами вида порождена процессами вида  , где , где  - любые опциональные марковские моменты, причём - любые опциональные марковские моменты, причём  , которые являются согласованными, непрерывными справа и имеющие левый предел. Поэтому нам осталось доказать, что каждый согласованный, непрерывный справа и имеющий предел слева процесс - опционален. , которые являются согласованными, непрерывными справа и имеющие левый предел. Поэтому нам осталось доказать, что каждый согласованный, непрерывный справа и имеющий предел слева процесс - опционален.
Пусть  - случайный процесс являющийся таковым. Для каждого, целого положительного числа - случайный процесс являющийся таковым. Для каждого, целого положительного числа  построим возрастающую последовательность моментов остановки следующим образом: построим возрастающую последовательность моментов остановки следующим образом:  для всех для всех  , причём если это множество пустое, то полагаем, что , причём если это множество пустое, то полагаем, что  . В силу теоремы . В силу теоремы  - прогрессивно измерим, поэтому - прогрессивно измерим, поэтому  тоже прогрессивно измерим. Значит тоже прогрессивно измерим. Значит  , где , где 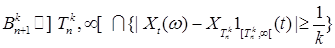 прогрессивно измерим. Заметим теперь, что прогрессивно измерим. Заметим теперь, что 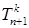 - м. о., поэтому из непрерывности справа процесса - м. о., поэтому из непрерывности справа процесса  получаем, что Р - п. н. получаем, что Р - п. н.  на множестве на множестве 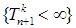 (попутно заметим, что непрерывность слева эквивалентна тому, что (попутно заметим, что непрерывность слева эквивалентна тому, что  для для 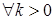 Р - п. н.). Обозначим для Р - п. н.). Обозначим для  Процесс Процесс  - опционален, поскольку он представляет собой сумму счётного числа опциональных процессов. Устремляя теперь - опционален, поскольку он представляет собой сумму счётного числа опциональных процессов. Устремляя теперь 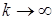 получим, что из непрерывности справа получим, что из непрерывности справа  Р - п. н., т. е. Р - п. н., т. е.  -опциональный процесс. Доказательство закончено. -опциональный процесс. Доказательство закончено.
4.3. Т еорема 22. Если процесс  - опционален, то множество - опционален, то множество  - тонкое (для - тонкое (для 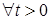 ). ).
Доказательство. Пусть  и по индукции определим и по индукции определим  Очевидно, что если Очевидно, что если  , то для любых фиксированных , то для любых фиксированных  . Ясно, что процесс . Ясно, что процесс  - непрерывен справа и согласован, a - непрерывен справа и согласован, a  - момент остановки. Заметим теперь, что множество - момент остановки. Заметим теперь, что множество  Поэтому Поэтому  где где 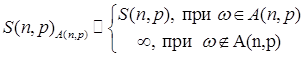 также является моментом остановки. Заметим, что из опциональности процесса также является моментом остановки. Заметим, что из опциональности процесса  следует, что Р - п. н. следует, что Р - п. н. 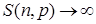 при при  . Поэтому . Поэтому 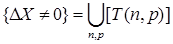 . Доказательство закончено. . Доказательство закончено.
Дата добавления: 2015-01-18 | Просмотры: 787 | Нарушение авторских прав
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|

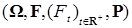 .
. алгеброй, обозначается через
алгеброй, обозначается через  называется
называется  где
где  — опциональный (предсказуемый) момент остановки.
— опциональный (предсказуемый) момент остановки.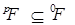 .
. со значениями в
со значениями в  называется опциональным (предсказуемым), если отображение
называется опциональным (предсказуемым), если отображение 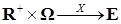 измеримо относительно
измеримо относительно  .
.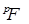 порождена всеми непрерывными слева согласованными процессами.
порождена всеми непрерывными слева согласованными процессами. , где
, где 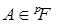 и
и  , где
, где  — любые опциональные марковские моменты, причём Р - п. н.
— любые опциональные марковские моменты, причём Р - п. н.  . Ясно, что эти процессы непрерывны слева и согласованы. Поэтому для доказательства теоремы достаточно доказать, что каждый непрерывный слева согласованный процесс
. Ясно, что эти процессы непрерывны слева и согласованы. Поэтому для доказательства теоремы достаточно доказать, что каждый непрерывный слева согласованный процесс 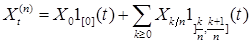 . Процесс
. Процесс  - предсказуем и непрерывен слева и поэтому
- предсказуем и непрерывен слева и поэтому 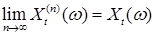 Р - п. н. Значит
Р - п. н. Значит  порождена процессами вида
порождена процессами вида  построим возрастающую последовательность моментов остановки следующим образом:
построим возрастающую последовательность моментов остановки следующим образом:  для всех
для всех  , причём если это множество пустое, то полагаем, что
, причём если это множество пустое, то полагаем, что  . В силу теоремы
. В силу теоремы  - прогрессивно измерим, поэтому
- прогрессивно измерим, поэтому  тоже прогрессивно измерим. Значит
тоже прогрессивно измерим. Значит  , где
, где 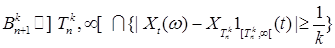 прогрессивно измерим. Заметим теперь, что
прогрессивно измерим. Заметим теперь, что 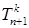 - м. о., поэтому из непрерывности справа процесса
- м. о., поэтому из непрерывности справа процесса  на множестве
на множестве 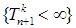 (попутно заметим, что непрерывность слева эквивалентна тому, что
(попутно заметим, что непрерывность слева эквивалентна тому, что  для
для 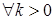 Р - п. н.). Обозначим для
Р - п. н.). Обозначим для  Процесс
Процесс  - опционален, поскольку он представляет собой сумму счётного числа опциональных процессов. Устремляя теперь
- опционален, поскольку он представляет собой сумму счётного числа опциональных процессов. Устремляя теперь 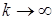 получим, что из непрерывности справа
получим, что из непрерывности справа  Р - п. н., т. е.
Р - п. н., т. е.  -опциональный процесс. Доказательство закончено.
-опциональный процесс. Доказательство закончено. - тонкое (для
- тонкое (для 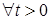 ).
). и по индукции определим
и по индукции определим  Очевидно, что если
Очевидно, что если  , то для любых фиксированных
, то для любых фиксированных  . Ясно, что процесс
. Ясно, что процесс  - непрерывен справа и согласован, a
- непрерывен справа и согласован, a  - момент остановки. Заметим теперь, что множество
- момент остановки. Заметим теперь, что множество  Поэтому
Поэтому  где
где 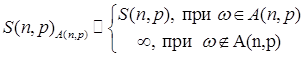 также является моментом остановки. Заметим, что из опциональности процесса
также является моментом остановки. Заметим, что из опциональности процесса 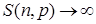 при
при  . Поэтому
. Поэтому 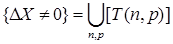 . Доказательство закончено.
. Доказательство закончено.