 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Очевидно, что
D x t = x t - x t- =
Таким образом, доказано утверждение. Теорема 47. Пусть 1) целочисленная случайная мера где 2) компенсатор
3) процесс
14.3. Замечание. В общем случае, если x t = x 0 + где
Дата добавления: 2015-01-18 | Просмотры: 658 | Нарушение авторских прав |

 . Учитывая, что траектория процесса
. Учитывая, что траектория процесса  кусочно-постоянна, получаем,
кусочно-постоянна, получаем,  . Поэтому
. Поэтому .
. опциональный процесс с кусочно-постоянными траекториями, конечным или счетным множеством состояний Е и матрицей интенсивности переходов
опциональный процесс с кусочно-постоянными траекториями, конечным или счетным множеством состояний Е и матрицей интенсивности переходов  размера -
размера -  . Тогда справедливы следующие утверждения:
. Тогда справедливы следующие утверждения: допускает представление
допускает представление  ,
, - последовательность марковских моментов (опциональных), исчерпывающая скачки процесса
- последовательность марковских моментов (опциональных), исчерпывающая скачки процесса  целочисленной случайной меры
целочисленной случайной меры  ;
; .
. , как легко показать, допускает представление
, как легко показать, допускает представление ,
,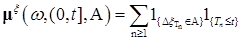 .
.