Абсолютная непрерывность вероятностных мер, соответствующих скачкообразным процессам
15.1. Определение. Пусть на измеримом пространстве  заданы две вероятностные меры заданы две вероятностные меры  , i = 1,2. Будем говорить, что мера , i = 1,2. Будем говорить, что мера  абсолютно непрерывна относительно меры абсолютно непрерывна относительно меры  и обозначать и обозначать  , если из того, что , если из того, что  следует, что следует, что  . .
Из этого определения следует: если  , то , то
 . Очевидно, что достаточным условием . Очевидно, что достаточным условием  является следующее: является следующее:  для для  . .
Из теоремы Радона - Никодима следует, что если  , то существует F - измеримая функция , то существует F - измеримая функция  такая, что такая, что  , которую называют производной Радона - Никодима и обозначают , которую называют производной Радона - Никодима и обозначают  . .
Везде ниже интеграл по мере  будем обозначать через будем обозначать через  . .
Пусть имеется измеримое пространство  с фильтрацией с фильтрацией  , на котором заданы две вероятностные меры , на котором заданы две вероятностные меры  , i = 1,2. Через , i = 1,2. Через  обозначим сужение меры обозначим сужение меры  на на  , т. е. , т. е. 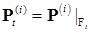 . Пусть . Пусть  , тогда существует в силу теоремы Радона – Никодима , тогда существует в силу теоремы Радона – Никодима  - процесс - процесс  называемый локальной плотностью называемый локальной плотностью  . .
Теорема 48. Пусть  - локальная плотность. Тогда - локальная плотность. Тогда  неотрицательный мартингал относительно меры неотрицательный мартингал относительно меры  , причем , причем  для для 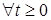 . .
Доказательство. Пусть 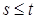 и и  . В силу условий теоремы . В силу условий теоремы  поэтому поэтому  . Так как . Так как  , то , то   . Значит . Значит
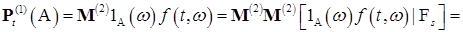
 . .
Отсюда в силу произвольности  получаем, что получаем, что 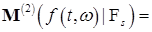   - п. н. Для завершения доказательства осталось заметить, что при - п. н. Для завершения доказательства осталось заметить, что при   для для 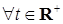 . .
15.3. Рассмотрим опциональный случайный процесс  , опреде-ленный на стохастическом базисе , опреде-ленный на стохастическом базисе  со значениями в со значениями в  и для и для 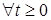 Р - п. н. допускающий представление Р - п. н. допускающий представление
 , (17) , (17)
где  опциональный случайный процесс с кусочно-постоянными траекториями и неслучайной опциональный случайный процесс с кусочно-постоянными траекториями и неслучайной  матрицей интенсивности перехода матрицей интенсивности перехода 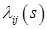 , причем , причем  ; ;  : :  - предсказуемая случайная функция такая, что - предсказуемая случайная функция такая, что
Р - п. н. 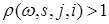 для для  . .
Сначала заметим, что  - предсказуемый процесс, так как - предсказуемый процесс, так как
 - опциональный. Из свойств интегралов, стоящих в правой части (17) следует - опциональный. Из свойств интегралов, стоящих в правой части (17) следует
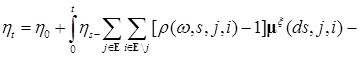
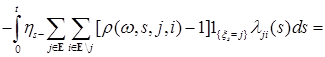
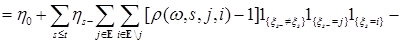
 . (18) . (18)
Пусть  - последовательность марковских моментов, исчерпывающая скачки процесса - последовательность марковских моментов, исчерпывающая скачки процесса  , ясно, что: а) , ясно, что: а) 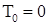 ; б) ; б)  на множестве на множестве  ; в) ; в)   . Тогда последнее равенство (18) можно записать в виде . Тогда последнее равенство (18) можно записать в виде
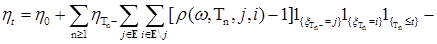
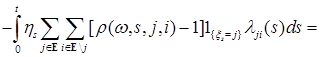

 . (18а) . (18а)
Отсюда следует, что в момент времени  происходит скачек у процесса происходит скачек у процесса 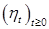 и его величина вычисляется по формуле и его величина вычисляется по формуле  . Поэтому Р - п. н. . Поэтому Р - п. н.
 . (19) . (19)
Пусть  , из (18) следует, что Р - п. н. , из (18) следует, что Р - п. н.
 . .
Очевидно, что
 . .
Далее в силу (18), имеем
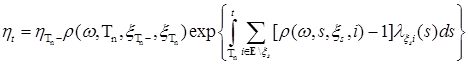 . .
Дата добавления: 2015-01-18 | Просмотры: 1228 | Нарушение авторских прав
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|

 заданы две вероятностные меры
заданы две вероятностные меры  , i = 1,2. Будем говорить, что мера
, i = 1,2. Будем говорить, что мера  абсолютно непрерывна относительно меры
абсолютно непрерывна относительно меры  и обозначать
и обозначать  , если из того, что
, если из того, что  следует, что
следует, что  .
. , то
, то . Очевидно, что достаточным условием
. Очевидно, что достаточным условием  для
для  .
. такая, что
такая, что  , которую называют производной Радона - Никодима и обозначают
, которую называют производной Радона - Никодима и обозначают  .
. .
. , на котором заданы две вероятностные меры
, на котором заданы две вероятностные меры  обозначим сужение меры
обозначим сужение меры  , т. е.
, т. е. 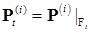 . Пусть
. Пусть  , тогда существует в силу теоремы Радона – Никодима
, тогда существует в силу теоремы Радона – Никодима  - процесс
- процесс  называемый локальной плотностью
называемый локальной плотностью  .
. - локальная плотность. Тогда
- локальная плотность. Тогда  неотрицательный мартингал относительно меры
неотрицательный мартингал относительно меры  для
для 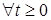 .
.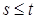 и
и  . В силу условий теоремы
. В силу условий теоремы  . Так как
. Так как  , то
, то 
 . Значит
. Значит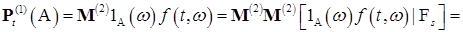
 .
.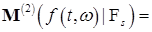


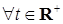 .
. , опреде-ленный на стохастическом базисе
, опреде-ленный на стохастическом базисе  со значениями в
со значениями в  и для
и для  , (17)
, (17) опциональный случайный процесс с кусочно-постоянными траекториями и неслучайной
опциональный случайный процесс с кусочно-постоянными траекториями и неслучайной  матрицей интенсивности перехода
матрицей интенсивности перехода 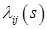 , причем
, причем  ;
;  :
:  - предсказуемая случайная функция такая, что
- предсказуемая случайная функция такая, что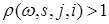 для
для  .
. - предсказуемый процесс, так как
- предсказуемый процесс, так как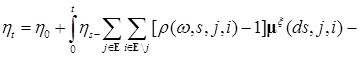
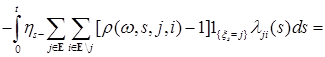
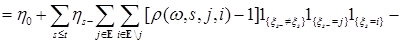
 . (18)
. (18) - последовательность марковских моментов, исчерпывающая скачки процесса
- последовательность марковских моментов, исчерпывающая скачки процесса 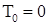 ; б)
; б)  на множестве
на множестве  ; в)
; в) 
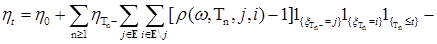
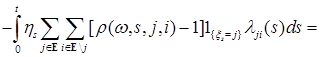

 . (18а)
. (18а) происходит скачек у процесса
происходит скачек у процесса 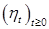 и его величина вычисляется по формуле
и его величина вычисляется по формуле  . Поэтому Р - п. н.
. Поэтому Р - п. н. . (19)
. (19) , из (18) следует, что Р - п. н.
, из (18) следует, что Р - п. н. .
. .
.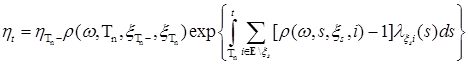 .
.