Процессы с ограниченной вариацией
5.1. Пусть  - стохастический базис. - стохастический базис.
Определение. Согласованный случайный процесс 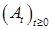 со значениями в со значениями в 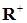 называется возрастающим, если почти все его траектории непрерывны справа и не убывают. Множество возрастающих процессов обозначим через называется возрастающим, если почти все его траектории непрерывны справа и не убывают. Множество возрастающих процессов обозначим через 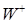 . .
Из определения возрастающего процесса следует, что:
а) возрастающий процесс имеет левый предел,
б) существует случайная величина  Р - п. н. Р - п. н.
5.2. Определение. Будем говорить, что согласованный процесс 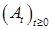 имеет ограниченную вариацию на отрезке [0,T], обозначаемую через Var имеет ограниченную вариацию на отрезке [0,T], обозначаемую через Var 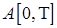 , если для любого разбиения , если для любого разбиения  отрезка [0,T] Р - п. н. конечна величина Var отрезка [0,T] Р - п. н. конечна величина Var 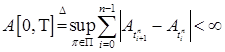 , где П - множество разбиений отрезка [0,T]. , где П - множество разбиений отрезка [0,T].
5.3. Определение. Через W обозначим множество непрерывных справа, имеющих левый предел случайных процессов таких, что почти каждая его траектория имеет ограниченную вариацию на любом компактном множестве из 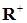 . .
Теорема 23. Согласованный случайный процесс  тогда и только тогда, когда тогда и только тогда, когда 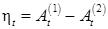 для для 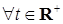 , где , где 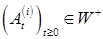 . (Докажите самостоятельно). . (Докажите самостоятельно).
Теорема 24. Пусть 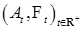 - возрастающий процесс. Тогда существует единственное разложение вида - возрастающий процесс. Тогда существует единственное разложение вида 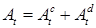 , где , где 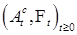 - непрерывный возрастающий процесс (т. е. предсказуемый), а - непрерывный возрастающий процесс (т. е. предсказуемый), а 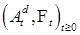 - опциональный случайный процесс. Если - опциональный случайный процесс. Если  - предсказуемый процесс, то - предсказуемый процесс, то 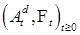 - предсказуемый процесс. - предсказуемый процесс.
Доказательство. Разложение 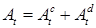 - следует из теоремы Лебега. Из доказательства теоремы 21 следует, что существует последовательность марковских моментов - следует из теоремы Лебега. Из доказательства теоремы 21 следует, что существует последовательность марковских моментов  , которая исчерпывает скачки процесса , которая исчерпывает скачки процесса 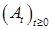 . Обозначим . Обозначим 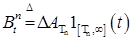 , , 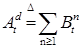 , где , где 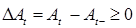 . Ясно, что при каждом п процесс . Ясно, что при каждом п процесс 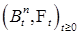 - возрастающий. Значит - возрастающий. Значит 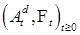 - возрастающий и непрерывен справа. Если - возрастающий и непрерывен справа. Если 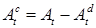 , то , то 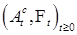 - непрерывный возрастающий процесс. Поскольку - непрерывный возрастающий процесс. Поскольку  - непрерывен справа и согласован, то в силу теоремы 15 он опционален. Доказательство закончено. - непрерывен справа и согласован, то в силу теоремы 15 он опционален. Доказательство закончено.
5.4. Обозначим через 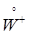 - множество интегрируемых возрастающих процессов, т. е. - множество интегрируемых возрастающих процессов, т. е. 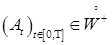 , если , если 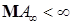 . Через . Через  обозначим множество интегрируемых возрастающих процессов, т. е. обозначим множество интегрируемых возрастающих процессов, т. е. 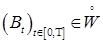 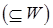 , если M Var , если M Var  . .
§6 Точечные случайные процессы. Формула Ито для считающихпроцессов. Компенсаторы.
6.1. Определение. Пусть на стохастическом базисе  задана последовательность марковских моментов задана последовательность марковских моментов 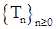 , которую мы будем называть точечным процессом, если выполняются условия: а) , которую мы будем называть точечным процессом, если выполняются условия: а) 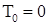 , ,
б) Р - п. н. 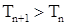 для для 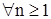 , в) существует , в) существует 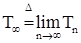 Р - п. н. Р - п. н.
Точечный процесс часто называют моновариантным процессом, процессом накопления или считающим процессом. Это связано со следующим обстоятельством.
Определим процесс 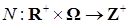 следующим образом: следующим образом: 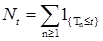 , где , где  - последовательность марковских моментов, фигурирующая в определении точечного процесса, и назовем его считающим процессом. Ясно, что процесс - последовательность марковских моментов, фигурирующая в определении точечного процесса, и назовем его считающим процессом. Ясно, что процесс 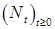 согласован с фильтрацией согласован с фильтрацией  , имеет кусочно-постоянные траектории, которые непрерывны справа и имеют левый предел. Поэтому в силу теоремы 19 он опционален и имеет конечное число скачков , имеет кусочно-постоянные траектории, которые непрерывны справа и имеют левый предел. Поэтому в силу теоремы 19 он опционален и имеет конечное число скачков 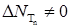 ( (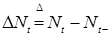 ) нa конечном интервале. Из определения считающего процесса следует, что ) нa конечном интервале. Из определения считающего процесса следует, что 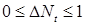 для для 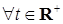 и и  при при 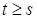 , поэтому он имеет: , поэтому он имеет:
а) ограниченную вариацию, б) является субмартингалом так как 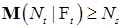 . Из сказанного выше следует, что между точечным и считающим процессом существует взаимно однозначное соответствие, так как . Из сказанного выше следует, что между точечным и считающим процессом существует взаимно однозначное соответствие, так как 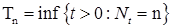 - опциональные марковские моменты обладают следующими свойствами: а) - опциональные марковские моменты обладают следующими свойствами: а) 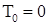 , б) Р - п. н. , б) Р - п. н. 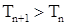 для для 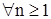 , ,
в) существует 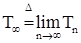 Р - п. н. Так как Р - п. н. Так как 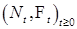 - субмартингал, то в силу теоремы Дуба - Мейера справедливо единственное разложение - субмартингал, то в силу теоремы Дуба - Мейера справедливо единственное разложение
Р - п. н.  для для 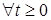 , где , где  - предсказуемый возрастающий процесс, а - предсказуемый возрастающий процесс, а 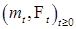 - мартингал, относительно меры Р. - мартингал, относительно меры Р.
6.2. Определение. Предсказуемый возрастающий процесс  назовём назовём 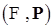 - компенсатором считающего случайного процесса - компенсатором считающего случайного процесса 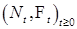 , если , если 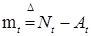 - мартингал относительно потока - мартингал относительно потока  и меры Р. и меры Р.
Пример. Пусть 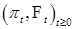 - пуассоновский процесс с интенсивностью - пуассоновский процесс с интенсивностью 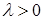 . Тогда его компенсатором является процесс . Тогда его компенсатором является процесс 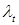 . .
6.3. Для формулировки дальнейших результатов нам понадобится конструкция интеграла Римана - Стилтьеса. Напомним ее. Пусть 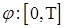 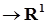 - непрерывная слева функция, а - непрерывная слева функция, а 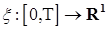 - непрерывная справа функция ограниченной вариации. Пусть - непрерывная справа функция ограниченной вариации. Пусть  - разбиение отрезка [0,T], т. е. - разбиение отрезка [0,T], т. е. 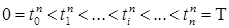 , причём , причём 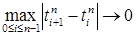 при при 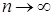 . Составим интегральную сумму . Составим интегральную сумму 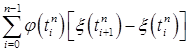 . Если при . Если при
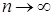 эта сумма стремиться к некоторому пределу, не зависящему от выбора способа разбиения отрезка [0,T], то этот предел называется интегралом Римана - Стилтьеса функции j по функции ограниченной вариации x и обозначается символом эта сумма стремиться к некоторому пределу, не зависящему от выбора способа разбиения отрезка [0,T], то этот предел называется интегралом Римана - Стилтьеса функции j по функции ограниченной вариации x и обозначается символом 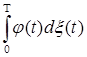 . Очевидно следующее утверждение. . Очевидно следующее утверждение.
Теорема 25. Если 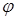 - предсказуемая функция на [0,T], а - предсказуемая функция на [0,T], а 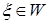 , то интеграл Римана - Стилтьеса , то интеграл Римана - Стилтьеса 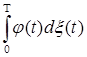 существует. существует.
Приведём без доказательства ряд свойств этого интеграла:
1) 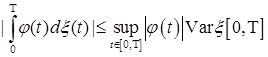 ; ;
2) если 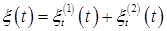 , где , где 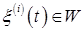 , то , то 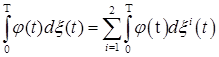 ; ;
3) если 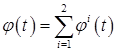 , где , где 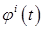 - предсказуемые функции, а - предсказуемые функции, а 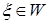 , то , то 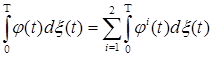 ; ;
4) 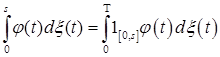 . .
6.4. Перейдем теперь к формулировке формулы Ито для считающего процесса 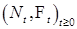 . .
Теорема 26. Пусть 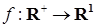 - измеримая ограниченная функция, a - измеримая ограниченная функция, a 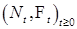 - считающий процесс. Тогда P - п. н. - считающий процесс. Тогда P - п. н.
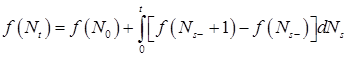 , (4) , (4)
где интеграл, стоящий в правой части (4), понимается в смысле Римана - Стилтьеса.
Доказательство.  - это марковские моменты - это марковские моменты  , которые исчерпывают скачки процесса , которые исчерпывают скачки процесса 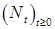 . Так как траектории процесса . Так как траектории процесса 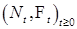 кусочнопостоянны, то справедливы равенства: кусочнопостоянны, то справедливы равенства:
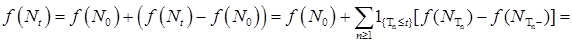
 . .
Учтем, что  ,имеем ,имеем
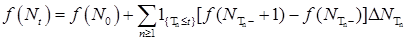 . .
Так как  , гдe , гдe 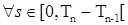 , то процесс , то процесс 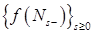 - предсказуем. В результате имеем (4). Доказательство закончено. - предсказуем. В результате имеем (4). Доказательство закончено.
Пример (применения формулы Ито). Вычислим интеграл Римана - Стилтьеса 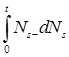 . .
Пусть 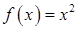 . Из (4) имеем . Из (4) имеем 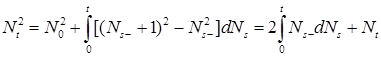 . .
Отсюда следует, что 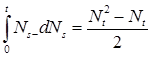 . .
6.5. Определение. Квадратической вариацией опционального процесса  , обозначаемая через , обозначаемая через 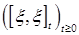 называется случайный процесс называется случайный процесс  . .
Если 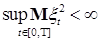 , то квадратическая вариация процесса , то квадратическая вариация процесса  является субмартингалом относительно меры Р и потока является субмартингалом относительно меры Р и потока  . Действительно, если . Действительно, если 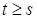 , то , то 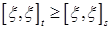 . Отсюда . Отсюда 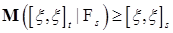 P - п.н. Поэтому, в силу теоремы Дуба - Мейера существует единственный предсказуемый процесс, обозначаемый через P - п.н. Поэтому, в силу теоремы Дуба - Мейера существует единственный предсказуемый процесс, обозначаемый через 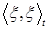 называется характеристикой такой, что называется характеристикой такой, что 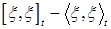 является мартингалом относительно меры Р и потока является мартингалом относительно меры Р и потока  . .
Пример. Вычислим квадратическую вариацию и характеристику точечного процесса  . .
1) 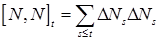 . Так как . Так как 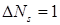 , то имеем , то имеем 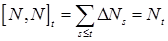 . .
2) 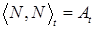 , где , где 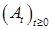 - компенсатор точечного процесса - компенсатор точечного процесса 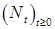 . .
6.6. Определение. Взаимной вариацией опциональных процессов  и и 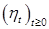 , обозначаемая , обозначаемая 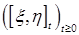 , называется опциональный процесс, определяемый равенством , называется опциональный процесс, определяемый равенством 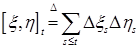 . .
Теорема 27. Пусть существуют 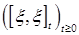 и и 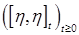 . Тогда существует . Тогда существует 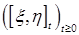 . .
Доказательство следует из равенства
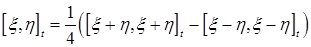 . .
Следствие 28. Пусть имеется два опциональных процесса, имеющих ограниченную вариацию 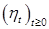 и и  . Тогда справедливо равенство P - п.н. . Тогда справедливо равенство P - п.н.  . .
Докажите самостоятельно.
6.7. Определение. Взаимной характеристикой квадратично-интегрируемых мартингалов  и и 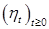 (относительно потока (относительно потока  и меры Р) называется предсказуемый случайный процесс обозначаемый через и меры Р) называется предсказуемый случайный процесс обозначаемый через 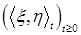 такой, что такой, что 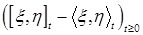 является мартингалом относительно потока является мартингалом относительно потока  и меры Р. и меры Р.
Заметим, что существование процесса 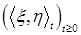 следует из теоремы Дуба - Мейера. следует из теоремы Дуба - Мейера.
Дата добавления: 2015-01-18 | Просмотры: 1116 | Нарушение авторских прав
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|

 - стохастический базис.
- стохастический базис.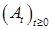 со значениями в
со значениями в 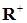 называется возрастающим, если почти все его траектории непрерывны справа и не убывают. Множество возрастающих процессов обозначим через
называется возрастающим, если почти все его траектории непрерывны справа и не убывают. Множество возрастающих процессов обозначим через 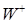 .
. Р - п. н.
Р - п. н.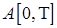 , если для любого разбиения
, если для любого разбиения  отрезка [0,T] Р - п. н. конечна величина Var
отрезка [0,T] Р - п. н. конечна величина Var 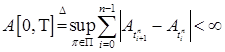 , где П - множество разбиений отрезка [0,T].
, где П - множество разбиений отрезка [0,T]. тогда и только тогда, когда
тогда и только тогда, когда 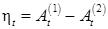 для
для 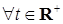 , где
, где 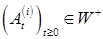 . (Докажите самостоятельно).
. (Докажите самостоятельно).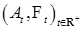 - возрастающий процесс. Тогда существует единственное разложение вида
- возрастающий процесс. Тогда существует единственное разложение вида 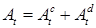 , где
, где 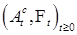 - непрерывный возрастающий процесс (т. е. предсказуемый), а
- непрерывный возрастающий процесс (т. е. предсказуемый), а 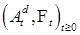 - опциональный случайный процесс. Если
- опциональный случайный процесс. Если  - предсказуемый процесс, то
- предсказуемый процесс, то  , которая исчерпывает скачки процесса
, которая исчерпывает скачки процесса 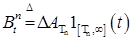 ,
, 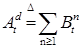 , где
, где 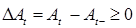 . Ясно, что при каждом п процесс
. Ясно, что при каждом п процесс 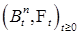 - возрастающий. Значит
- возрастающий. Значит 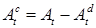 , то
, то 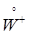 - множество интегрируемых возрастающих процессов, т. е.
- множество интегрируемых возрастающих процессов, т. е. 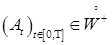 , если
, если 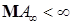 . Через
. Через  обозначим множество интегрируемых возрастающих процессов, т. е.
обозначим множество интегрируемых возрастающих процессов, т. е. 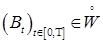
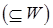 , если M Var
, если M Var  .
.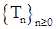 , которую мы будем называть точечным процессом, если выполняются условия: а)
, которую мы будем называть точечным процессом, если выполняются условия: а) 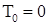 ,
,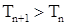 для
для 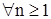 , в) существует
, в) существует 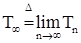 Р - п. н.
Р - п. н.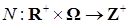 следующим образом:
следующим образом: 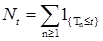 , где
, где 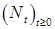 согласован с фильтрацией
согласован с фильтрацией  , имеет кусочно-постоянные траектории, которые непрерывны справа и имеют левый предел. Поэтому в силу теоремы 19 он опционален и имеет конечное число скачков
, имеет кусочно-постоянные траектории, которые непрерывны справа и имеют левый предел. Поэтому в силу теоремы 19 он опционален и имеет конечное число скачков 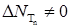 (
(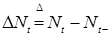 ) нa конечном интервале. Из определения считающего процесса следует, что
) нa конечном интервале. Из определения считающего процесса следует, что 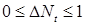 для
для  при
при 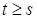 , поэтому он имеет:
, поэтому он имеет: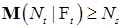 . Из сказанного выше следует, что между точечным и считающим процессом существует взаимно однозначное соответствие, так как
. Из сказанного выше следует, что между точечным и считающим процессом существует взаимно однозначное соответствие, так как 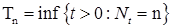 - опциональные марковские моменты обладают следующими свойствами: а)
- опциональные марковские моменты обладают следующими свойствами: а) 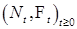 - субмартингал, то в силу теоремы Дуба - Мейера справедливо единственное разложение
- субмартингал, то в силу теоремы Дуба - Мейера справедливо единственное разложение для
для 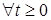 , где
, где 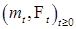 - мартингал, относительно меры Р.
- мартингал, относительно меры Р.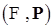 - компенсатором считающего случайного процесса
- компенсатором считающего случайного процесса 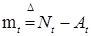 - мартингал относительно потока
- мартингал относительно потока 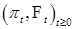 - пуассоновский процесс с интенсивностью
- пуассоновский процесс с интенсивностью 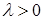 . Тогда его компенсатором является процесс
. Тогда его компенсатором является процесс 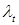 .
.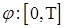
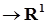 - непрерывная слева функция, а
- непрерывная слева функция, а 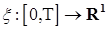 - непрерывная справа функция ограниченной вариации. Пусть
- непрерывная справа функция ограниченной вариации. Пусть  - разбиение отрезка [0,T], т. е.
- разбиение отрезка [0,T], т. е. 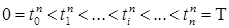 , причём
, причём 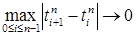 при
при 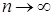 . Составим интегральную сумму
. Составим интегральную сумму 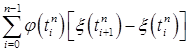 . Если при
. Если при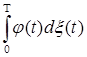 . Очевидно следующее утверждение.
. Очевидно следующее утверждение.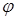 - предсказуемая функция на [0,T], а
- предсказуемая функция на [0,T], а 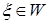 , то интеграл Римана - Стилтьеса
, то интеграл Римана - Стилтьеса 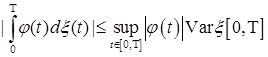 ;
;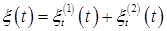 , где
, где 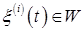 , то
, то 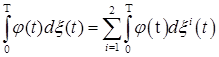 ;
;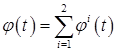 , где
, где 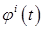 - предсказуемые функции, а
- предсказуемые функции, а 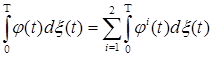 ;
;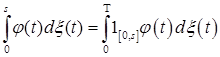 .
.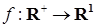 - измеримая ограниченная функция, a
- измеримая ограниченная функция, a 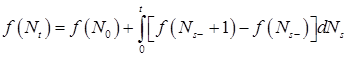 , (4)
, (4) - это марковские моменты
- это марковские моменты 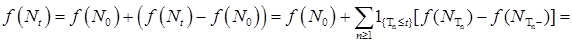
 .
. ,имеем
,имеем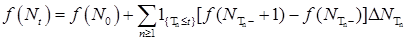 .
. , гдe
, гдe 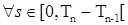 , то процесс
, то процесс 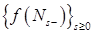 - предсказуем. В результате имеем (4). Доказательство закончено.
- предсказуем. В результате имеем (4). Доказательство закончено.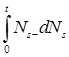 .
.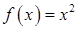 . Из (4) имеем
. Из (4) имеем 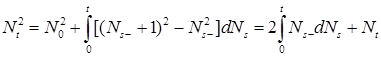 .
.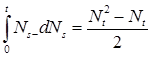 .
. , обозначаемая через
, обозначаемая через 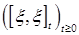 называется случайный процесс
называется случайный процесс  .
.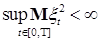 , то квадратическая вариация процесса
, то квадратическая вариация процесса  . Действительно, если
. Действительно, если 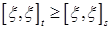 . Отсюда
. Отсюда 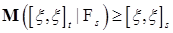 P - п.н. Поэтому, в силу теоремы Дуба - Мейера существует единственный предсказуемый процесс, обозначаемый через
P - п.н. Поэтому, в силу теоремы Дуба - Мейера существует единственный предсказуемый процесс, обозначаемый через 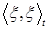 называется характеристикой такой, что
называется характеристикой такой, что 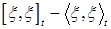 является мартингалом относительно меры Р и потока
является мартингалом относительно меры Р и потока  .
.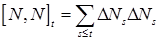 . Так как
. Так как 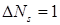 , то имеем
, то имеем 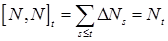 .
.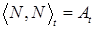 , где
, где 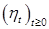 , обозначаемая
, обозначаемая 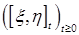 , называется опциональный процесс, определяемый равенством
, называется опциональный процесс, определяемый равенством 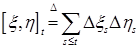 .
.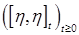 . Тогда существует
. Тогда существует 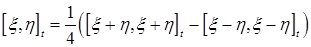 .
. .
.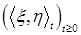 такой, что
такой, что 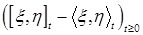 является мартингалом относительно потока
является мартингалом относительно потока