Полумартингалы
2.1. Определение. Будем говорить, что процесс  - мартингал, если выполняются условия: 1) - мартингал, если выполняются условия: 1)  , 2) , 2)  Р - п. н., Р - п. н.,  и и  . .
Будем говорить, что  - супермартингал, если: 1) - супермартингал, если: 1)  , 2) , 2)  Р - п. н. для Р - п. н. для  и и  . .
Процесс  субмартингал, если: 1) субмартингал, если: 1)  , 2) , 2)  Р - п. н. для Р - п. н. для  и и  . .
Множество случайных процессов, являющихся "суб", "супер", или просто мартингалами называется полумартингалами. Множество полумартингалов обозначим через  . .
Пример. Рассмотрим пуассоновский процесс 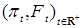 . Из его определения следует, что . Из его определения следует, что  для для  . Поэтому . Поэтому  . Следовательно, пуассоновский процесс - субмартингал. . Следовательно, пуассоновский процесс - субмартингал.
Ниже мы покажем, что если  , то он допускает представление , то он допускает представление 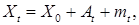 где где  - процесс имеющий ограниченную вариацию, а - процесс имеющий ограниченную вариацию, а  - мартингал. - мартингал.
2.2. Определение. Случайный процесс  называется предсказуемым, если его траектории непрерывны слева, имеют предел справа и не имеют разрывов второго рода. называется предсказуемым, если его траектории непрерывны слева, имеют предел справа и не имеют разрывов второго рода.
Теорема 5 (Дуба - Мейера). Пусть  - субмартингал относительно меры Р. Тогда существует единственный предсказуемый возрастающий процесс - субмартингал относительно меры Р. Тогда существует единственный предсказуемый возрастающий процесс  такой, что для любого такой, что для любого  Р - п. н. Р - п. н. 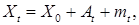
где  - мартингал. - мартингал.
(Без доказательства.)
Замечание. Если  - супермартингал, то - супермартингал, то  - субмартингал. Следовательно - субмартингал. Следовательно  значит значит 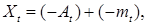 из из  где где  . .
Пример. Пусть  - пуассоновский процесс, тогда - пуассоновский процесс, тогда  Р - п. н. для Р - п. н. для 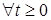 , где , где  - мартингал относительно меры Р. - мартингал относительно меры Р.
2.3. Определение. Мартингал 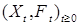 относительно меры Р называется регулярным, если существует относительно меры Р называется регулярным, если существует  -измеримая случайная величина -измеримая случайная величина  , такая, что , такая, что  Р - п. н. Р - п. н.  для для 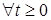 . .
2.3.1. Замечание. Очевидно, что регулярность мартингала 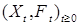 относительно меры Р эквивалентна требованию равномерной интегрируемости семейства относительно меры Р эквивалентна требованию равномерной интегрируемости семейства  . .
2.3.2. Теорема 6. Пусть 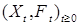 регулярный мартингал относительно меры Р, а семейство регулярный мартингал относительно меры Р, а семейство 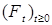 непрерывно справа. Тогда у процесса непрерывно справа. Тогда у процесса 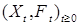 существует модификация существует модификация  с траекториями непрерывными справа и имеющими левый предел. с траекториями непрерывными справа и имеющими левый предел.
Доказательство. Так как 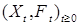 - регулярный мартингал, существует - регулярный мартингал, существует  - измеримая интегрируемая случайная величина - измеримая интегрируемая случайная величина  такая, что такая, что  . Тогда для каждого . Тогда для каждого  имеем Р - п. н. имеем Р - п. н.
 . .
Поэтому, если положить  , то получим непрерывную справа модификацию. , то получим непрерывную справа модификацию.
Покажем теперь, что существует левый предел. Действительно, если бы с положительной вероятностью этот предел не существовал, то тогда среднее число пересечений отрезка  снизу вверх за время снизу вверх за время  обозначаемое через обозначаемое через  было бы равно было бы равно 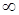 , но , но  . Указанное противоречие довершает доказательство теоремы. . Указанное противоречие довершает доказательство теоремы.
2.4. Приведем теперь условия существования непрерывной справа модификации у супермартингала.
Теорема 7. Пусть 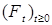 - непрерывно справа, а - непрерывно справа, а 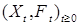 супермартингал относительно меры Р. Супермартингал супермартингал относительно меры Р. Супермартингал 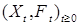 имеет непрерывную справа модификацию тогда и только тогда, когда функция времени имеет непрерывную справа модификацию тогда и только тогда, когда функция времени 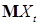 непрерывна справа. непрерывна справа.
Доказательство. В силу условий теоремы  Р - п. н., а из того, что Р - п. н., а из того, что  , имеем , имеем 
Р - п. н. для 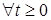 . .
Отметим  Р - п. н. тогда и только тогда, когда Р - п. н. тогда и только тогда, когда  . .
Пусть 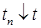 . Так как . Так как  равномерно интегрируемо, то равномерно интегрируемо, то  . Стало быть, . Стало быть,  Р - п. н. тогда и только тогда, когда Р - п. н. тогда и только тогда, когда  . Поскольку . Поскольку  как функция как функция  убывает, то это равносильно ее непрерывности справа в точке убывает, то это равносильно ее непрерывности справа в точке  . .
Пусть  - непрерывная справа модификация супермартингала - непрерывная справа модификация супермартингала  . Тогда . Тогда  для каждого для каждого  (как функция времени, в силу приведенных выше рассуждений) непрерывна справа. Обратно, если функция времени (как функция времени, в силу приведенных выше рассуждений) непрерывна справа. Обратно, если функция времени 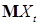 непрерывна справа, то процесс непрерывна справа, то процесс  представляет собой непрерывную справа модификацию. Доказательство закончено. представляет собой непрерывную справа модификацию. Доказательство закончено.
2.5. В дальнейшем нам понадобится неравенство Колмогорова для квадратично интегрируемых мартингалов.
Определение. Мартингал 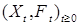 относительно меры Р назовем квадратично интегрируемым, если относительно меры Р назовем квадратично интегрируемым, если  . .
Теорема 8 (неравенство Колмогорова). Пусть 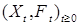 – квадратично интегрируемый мартингал. Тогда для любого – квадратично интегрируемый мартингал. Тогда для любого 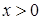
 . .
Доказательство. Пусть  , где , где  . Очевидно, что . Очевидно, что  и и 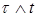 - марковские моменты, причем - марковские моменты, причем  Р - п. н. Поэтому Р - п. н. Поэтому  . Заметим теперь, что . Заметим теперь, что 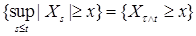 . .
Поэтому в силу неравенства Чебышева, имеем  . .
Доказательство закончено.
2.6. Далее нам понадобится одно неравенство для квадратично интегрируемых мартингалов.
Теорема 9. Пусть  квадратично интегрируемый мартингал относительно меры Р. Тогда квадратично интегрируемый мартингал относительно меры Р. Тогда
 (3) (3)
Доказательство. В силу теоремы 8 для  , имеем , имеем

Поэтому

Отсюда в силу неравенства Коши - Буняковского, имеем
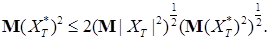
Стало быть  отсюда следует утверждение теоремы. отсюда следует утверждение теоремы.
Дата добавления: 2015-01-18 | Просмотры: 860 | Нарушение авторских прав
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|

 - мартингал, если выполняются условия: 1)
- мартингал, если выполняются условия: 1)  , 2)
, 2)  Р - п. н.,
Р - п. н.,  и
и  .
. Р - п. н. для
Р - п. н. для  Р - п. н. для
Р - п. н. для  .
.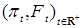 . Из его определения следует, что
. Из его определения следует, что  для
для  . Следовательно, пуассоновский процесс - субмартингал.
. Следовательно, пуассоновский процесс - субмартингал. , то он допускает представление
, то он допускает представление 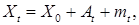 где
где  - процесс имеющий ограниченную вариацию, а
- процесс имеющий ограниченную вариацию, а  - мартингал.
- мартингал. называется предсказуемым, если его траектории непрерывны слева, имеют предел справа и не имеют разрывов второго рода.
называется предсказуемым, если его траектории непрерывны слева, имеют предел справа и не имеют разрывов второго рода. - субмартингал относительно меры Р. Тогда существует единственный предсказуемый возрастающий процесс
- субмартингал относительно меры Р. Тогда существует единственный предсказуемый возрастающий процесс  такой, что для любого
такой, что для любого  Р - п. н.
Р - п. н.  - супермартингал, то
- супермартингал, то  - субмартингал. Следовательно
- субмартингал. Следовательно  значит
значит 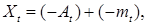 из
из  где
где  .
. - пуассоновский процесс, тогда
- пуассоновский процесс, тогда  Р - п. н. для
Р - п. н. для 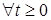 , где
, где 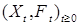 относительно меры Р называется регулярным, если существует
относительно меры Р называется регулярным, если существует  -измеримая случайная величина
-измеримая случайная величина  , такая, что
, такая, что  Р - п. н.
Р - п. н.  для
для 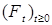 непрерывно справа. Тогда у процесса
непрерывно справа. Тогда у процесса  с траекториями непрерывными справа и имеющими левый предел.
с траекториями непрерывными справа и имеющими левый предел. .
. , то получим непрерывную справа модификацию.
, то получим непрерывную справа модификацию. снизу вверх за время
снизу вверх за время  обозначаемое через
обозначаемое через  было бы равно
было бы равно 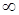 , но
, но  . Указанное противоречие довершает доказательство теоремы.
. Указанное противоречие довершает доказательство теоремы.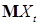 непрерывна справа.
непрерывна справа. Р - п. н., а из того, что
Р - п. н., а из того, что  , имеем
, имеем 
 Р - п. н. тогда и только тогда, когда
Р - п. н. тогда и только тогда, когда  .
.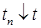 . Так как
. Так как  равномерно интегрируемо, то
равномерно интегрируемо, то  . Стало быть,
. Стало быть,  . Поскольку
. Поскольку  как функция
как функция  убывает, то это равносильно ее непрерывности справа в точке
убывает, то это равносильно ее непрерывности справа в точке  - непрерывная справа модификация супермартингала
- непрерывная справа модификация супермартингала  для каждого
для каждого  представляет собой непрерывную справа модификацию. Доказательство закончено.
представляет собой непрерывную справа модификацию. Доказательство закончено. .
.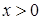
 .
. , где
, где  . Очевидно, что
. Очевидно, что  и
и 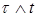 - марковские моменты, причем
- марковские моменты, причем  Р - п. н. Поэтому
Р - п. н. Поэтому  . Заметим теперь, что
. Заметим теперь, что 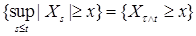 .
. .
. квадратично интегрируемый мартингал относительно меры Р. Тогда
квадратично интегрируемый мартингал относительно меры Р. Тогда (3)
(3) , имеем
, имеем

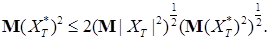
 отсюда следует утверждение теоремы.
отсюда следует утверждение теоремы.