Марковские моменты. Локальные полумартингалы
4.1. Определение. Отображение 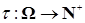 называется марковским моментом, если называется марковским моментом, если 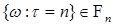 для для 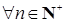 . .
Конечный марковский момент (Р ( )=1) называется моментом остановки. )=1) называется моментом остановки.
Обозначим 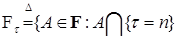 для всех для всех 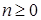 }. }.
Предложение 11.  алгебра. алгебра.
Доказательство. Очевидно, что: i) 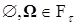 ; ii) ; ii)  замкнута относительно операции взятия счетных пересечений; iii) если замкнута относительно операции взятия счетных пересечений; iii) если 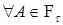 и и  , то , то 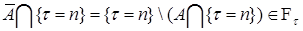 и следовательно и следовательно 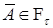 . Стало быть, . Стало быть,  алгебра. алгебра.
Примеры: 1) 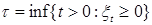 . .
2) Пусть 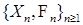 - случайная последовательность, а - случайная последовательность, а 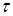 -марковский момент. Определим -марковский момент. Определим 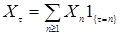 , где , где 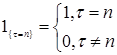 Тогда Тогда 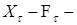 измерима. (Докажите самостоятельно). измерима. (Докажите самостоятельно).
3) Пусть 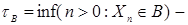 марковский момент. Действительно марковский момент. Действительно
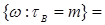  . .
Предложение 10. Пусть 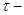 марковский момент. Тогда 1) марковский момент. Тогда 1) 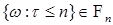 , 2) , 2) 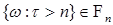
Доказательство. 1) Очевидно 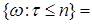 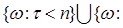  . Поэтому из определения марковского момента следует, что . Поэтому из определения марковского момента следует, что  . Второе утверждение очевидно. . Второе утверждение очевидно.
4.2. Пусть 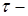 марковский момент относительно фильтрации марковский момент относительно фильтрации 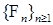 . .
Предложение 12. 1) Если t, s - марковские моменты, то  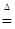 min(t,s), min(t,s),
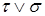 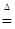 max(s,t), t+s, (t-s)+ max(s,t), t+s, (t-s)+ 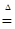 max(t-s,0) являются марковскими моментами. max(t-s,0) являются марковскими моментами.
2) Если 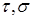 - марковские моменты и - марковские моменты и 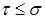 Р - п. н., то Р - п. н., то  . .
3) Если 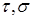 - марковские моменты, то - марковские моменты, то 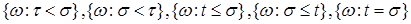 принадлежат принадлежат 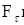 и и 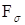 . .
4) Если 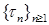 - последовательность марковских моментов. Тогда - последовательность марковских моментов. Тогда 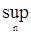 tn, tn, 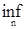 tn, tn, 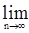 tn , tn , 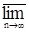 tn, tn,  tn также являются марковскими моментами. tn также являются марковскими моментами.
Докажите предложение 12 самостоятельно.
4.3. Определение. Последовательность  называется остановленной, если называется остановленной, если 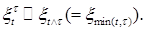
Определение. Последовательность марковских моментов 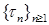 называется t-локализующей, если она неубывающая и Р - п. н. существует t = называется t-локализующей, если она неубывающая и Р - п. н. существует t = 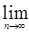 tn. Если tn. Если 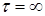 ¥, то ¥, то 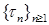 называется локализующей. называется локализующей.
4.4. Определение. Последовательность  называется локальным полумартингалом, если существует локализующая последовательность называется локальным полумартингалом, если существует локализующая последовательность 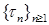 , такая, что остановленная последовательность , такая, что остановленная последовательность  является полумартингалом. является полумартингалом.
Определение. Последовательность 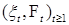 называется мартингал-разностью, если существует М (xt | называется мартингал-разностью, если существует М (xt | 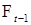 ) для любого ) для любого 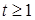 и М ( и М (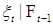 ) =0 Р - п. н. ) =0 Р - п. н.
Из этого определения следует утверждение.
Предложение 13. Последовательность  , где , где 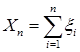 является мартингалом (относительно меры Р) тогда и только тогда, когда является мартингалом (относительно меры Р) тогда и только тогда, когда 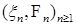 является мартингал разностью. является мартингал разностью.
4.5. Лемма 14. Пусть  - локальный мартингал с - локальный мартингал с  и и 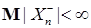 либо либо 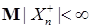 . Тогда . Тогда  - мартингал. - мартингал.
Доказательство. Сначала покажем, что если выполнено 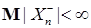 , то , то 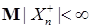 и следовательно и следовательно  , для , для 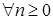 . Действительно. Пусть . Действительно. Пусть 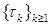 - локализующая последовательность, тогда в силу леммы Фату имеем - локализующая последовательность, тогда в силу леммы Фату имеем
М 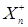 = М = М   £ £  М М  = =  М [ М [ 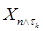 + + 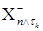 ] = ] = 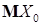 + +  М М 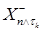 £ | £ | 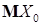 | + | +  < ¥. Поэтому < ¥. Поэтому 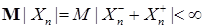 . .
Заметим, что: а) | 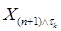 | £ | £  ; б) M ; б) M  <¥. Из того, что <¥. Из того, что  - локальный мартингал, следует М ( - локальный мартингал, следует М (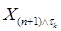 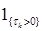 | | 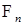 )= )= 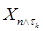 Р - п. н.. Воспользуемся теперь теоремой Лебега (о мажорируемой сходимости), в последнем равенстве имеем Р - п. н.. Воспользуемся теперь теоремой Лебега (о мажорируемой сходимости), в последнем равенстве имеем 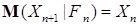 Р - п.н.. Р - п.н..
Доказательство закончено.
Следствие 15. Всякий локальный мартингал ограниченный сверху (снизу) является мартингалом.
Теорема 16. Пусть  - локальный мартингал (относительно меры Р). Тогда последовательность - локальный мартингал (относительно меры Р). Тогда последовательность  является супермартингалом (относительно меры Р). является супермартингалом (относительно меры Р).
Доказательство. В силу условий существует локализующая последовательность марковских моментов 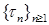 такая, что такая, что 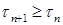
P - п. н., причем 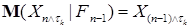 Р - п. н. Поэтому в силу леммы Фату, имеем P - п. н. Р - п. н. Поэтому в силу леммы Фату, имеем P - п. н.
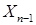 = =  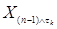 = =  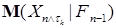 ³ M( ³ M(  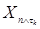 | | 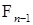 ) = ) =
=  . .
Доказательство закончено.
Дата добавления: 2015-01-18 | Просмотры: 801 | Нарушение авторских прав
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|

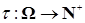 называется марковским моментом, если
называется марковским моментом, если 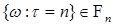 для
для 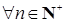 .
. )=1) называется моментом остановки.
)=1) называется моментом остановки.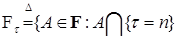 для всех
для всех 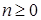 }.
}. алгебра.
алгебра.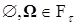 ; ii)
; ii)  замкнута относительно операции взятия счетных пересечений; iii) если
замкнута относительно операции взятия счетных пересечений; iii) если 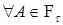 и
и  , то
, то 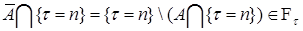 и следовательно
и следовательно 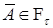 . Стало быть,
. Стало быть, 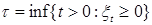 .
.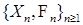 - случайная последовательность, а
- случайная последовательность, а 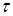 -марковский момент. Определим
-марковский момент. Определим 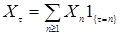 , где
, где 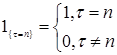 Тогда
Тогда 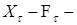 измерима. (Докажите самостоятельно).
измерима. (Докажите самостоятельно).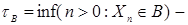 марковский момент. Действительно
марковский момент. Действительно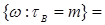
 .
.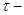 марковский момент. Тогда 1)
марковский момент. Тогда 1) 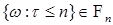 , 2)
, 2) 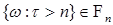
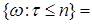
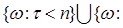
 . Поэтому из определения марковского момента следует, что
. Поэтому из определения марковского момента следует, что  . Второе утверждение очевидно.
. Второе утверждение очевидно.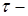 марковский момент относительно фильтрации
марковский момент относительно фильтрации 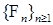 .
.
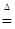 min(t,s),
min(t,s),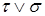
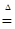 max(t-s,0) являются марковскими моментами.
max(t-s,0) являются марковскими моментами.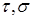 - марковские моменты и
- марковские моменты и 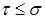 Р - п. н., то
Р - п. н., то  .
.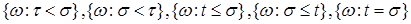 принадлежат
принадлежат 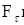 и
и 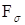 .
.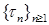 - последовательность марковских моментов. Тогда
- последовательность марковских моментов. Тогда 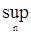 tn,
tn, 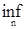 tn,
tn, 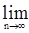 tn ,
tn , 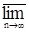 tn,
tn,  tn также являются марковскими моментами.
tn также являются марковскими моментами. называется остановленной, если
называется остановленной, если 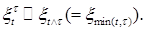
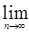 tn. Если
tn. Если 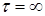 ¥, то
¥, то  называется локальным полумартингалом, если существует локализующая последовательность
называется локальным полумартингалом, если существует локализующая последовательность  является полумартингалом.
является полумартингалом.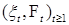 называется мартингал-разностью, если существует М (xt |
называется мартингал-разностью, если существует М (xt | 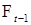 ) для любого
) для любого 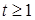 и М (
и М (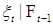 ) =0 Р - п. н.
) =0 Р - п. н. , где
, где 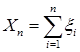 является мартингалом (относительно меры Р) тогда и только тогда, когда
является мартингалом (относительно меры Р) тогда и только тогда, когда 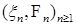 является мартингал разностью.
является мартингал разностью. и
и 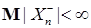 либо
либо 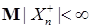 . Тогда
. Тогда  , для
, для 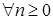 . Действительно. Пусть
. Действительно. Пусть 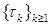 - локализующая последовательность, тогда в силу леммы Фату имеем
- локализующая последовательность, тогда в силу леммы Фату имеем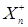 = М
= М 
 £
£ 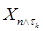 +
+ 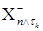 ] =
] = 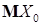 +
+ 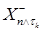 £ |
£ |  < ¥. Поэтому
< ¥. Поэтому 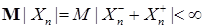 .
.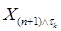 | £
| £  ; б) M
; б) M 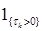 |
| 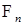 )=
)= 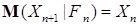 Р - п.н..
Р - п.н..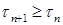
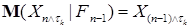 Р - п. н. Поэтому в силу леммы Фату, имеем P - п. н.
Р - п. н. Поэтому в силу леммы Фату, имеем P - п. н.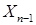 =
= 
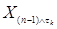 =
= 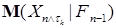 ³ M(
³ M( 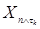 |
| 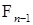 ) =
) = .
.