Мартингалы, супермартингалы, субмартингалы
3.1. Пусть ( , ,  , , 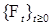 , Р) – стохастический базис, последовательность { , Р) – стохастический базис, последовательность { 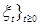 - согласована с потоком - согласована с потоком 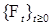 , и принимает значения в , и принимает значения в  . .
Определение. Последовательность ( , ,  ) t > 1 называется мартингалом, если: ) t > 1 называется мартингалом, если:
1)  , 2) , 2) 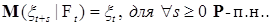
Если выполнено 1) и  Р -п. н., то последовательность ( Р -п. н., то последовательность ( , ,  ) t >0 называется супермартингалом. ) t >0 называется супермартингалом.
Если выполнено 1) и 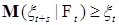 Р - п. н., то последовательность ( Р - п. н., то последовательность ( , ,  ) t >0 называется субмартингалом. ) t >0 называется субмартингалом.
Пример. Пусть  , где , где 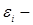 независимые в совокупности случайные величины. Пусть независимые в совокупности случайные величины. Пусть 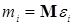 , ,  . Ясно, что . Ясно, что
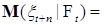  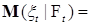 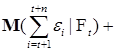  = =
=  + + 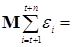  + + 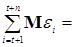  + + 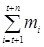 . .
Отсюда следует, что:
а) ( , ,  ) t > 1- мартингал, если ) t > 1- мартингал, если  для любого t; для любого t;
б) ( , ,  ) t > 1- супермартингал, если ) t > 1- супермартингал, если 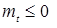 для любого t; для любого t;
в) ( , ,  ) t > 1- субмартингал, если ) t > 1- субмартингал, если 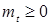 для любого t; для любого t;
Утверждение 5. Если ( , ,  ) t >0 – марковская случайная последовательность с переходной вероятностью P (s, ) t >0 – марковская случайная последовательность с переходной вероятностью P (s,  ,t,B), то ,t,B), то
P (s,  t,B) – мартингал для t,B) – мартингал для 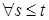 , относительно потока , относительно потока  алгебр алгебр  и меры Р. и меры Р.
Доказательство. Из соотношения Чепмена – Колмогорова имеем
Р -п. н. при  : :
M (P (u,  , t,B)| , t,B)| 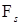 )= M (P (u, )= M (P (u,  , t,B)| , t,B)|  ) = ) = 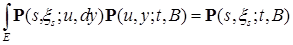 . .
3.2. Теорема 6 (Дуба). Пусть ( , ,  ) t >0 – неотрицательный супермартингал, тогда с вероятностью 1 существует ) t >0 – неотрицательный супермартингал, тогда с вероятностью 1 существует 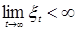 . .
Замечания. 1) Покажем, что предложения о неотрицательности супермартингала ( , ,  ) t >0 можно отказаться. Очевидно, что М ) t >0 можно отказаться. Очевидно, что М 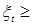 М М 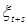 , т.е. в среднем последовательность , т.е. в среднем последовательность  - убывает. Пусть - убывает. Пусть  Образуем новую последовательность Образуем новую последовательность 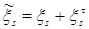 . Понятно, что . Понятно, что  .Тогда .Тогда  , значит любой супермартингал представим в виде разности двух неотрицательных супермартингалов. , значит любой супермартингал представим в виде разности двух неотрицательных супермартингалов.
2) Если 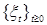 - супермартингал, то - супермартингал, то 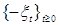 - субмартингал. Поэтому утверждение теоремы 6 верно и для субмартингалов. - субмартингал. Поэтому утверждение теоремы 6 верно и для субмартингалов.
3.2.1 Доказательство теоремы Дуба опирается на две вспомогательные леммы.
Пусть  числовая последовательность, a<b, [ a,b ] – отрезок. Обозначим числовая последовательность, a<b, [ a,b ] – отрезок. Обозначим  - число пересечений отрезка [ a,b ] последовательностью - число пересечений отрезка [ a,b ] последовательностью 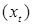 снизу вверх. снизу вверх.
Лемма 7 (О числе пересечений отрезка [ a,b ] снизу вверх).
Справедливо неравенство:
 , ,
где 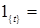 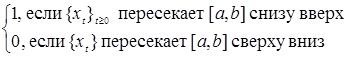
Доказательство. Обозначим
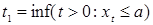 , ,  , ,
 , , 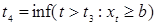 , ,
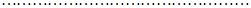
 , , 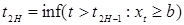
Очевидно, что 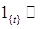 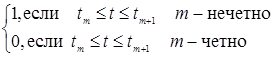
Отсюда следует, что
(b-a) 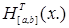 = = 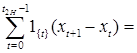 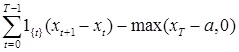 . .
Докзательство закончено.
Лемма 8. (О среднем числе пересечений). Пусть ( , ,  ) t >0 – неотрицательный супермартингал, тогда М ) t >0 – неотрицательный супермартингал, тогда М  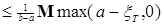 . .
Доказательство. В силу леммы 7 имеем неравенство:
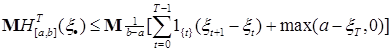 . .
Так как ( , ,  ) t >0 - супермартингал, то М ( ) t >0 - супермартингал, то М (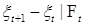 ) ≤ 0. Отсюда следует неравенство ) ≤ 0. Отсюда следует неравенство
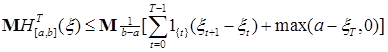  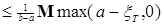 . Доказательство закончено. . Доказательство закончено.
3.2.2. Доказательство теоремы 6. Предположим, что у последовательности  не существует конечного предела. Через В обозначим множество не существует конечного предела. Через В обозначим множество 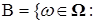 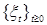 не имеет конечного предела}. Наше предположение выполнено, если: не имеет конечного предела}. Наше предположение выполнено, если:
1) 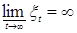 Р - п. н., Р - п. н.,
2) 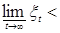 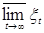 Р - п. н. Р - п. н.
Обозначим: А   }, C = }, C = 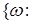  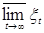 }. Очевидно, что }. Очевидно, что 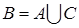 , поэтому , поэтому  . Значит для доказательства теоремы достаточно доказать, что Р (А) =0 и Р (С)=0. . Значит для доказательства теоремы достаточно доказать, что Р (А) =0 и Р (С)=0.
Покажем, что Р (А)=0. В силу неравенства Чебышева и леммы Фату имеем Р (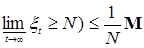  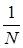 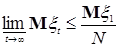 . Устремляя теперь . Устремляя теперь 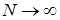 , получаем Р (А)=0. , получаем Р (А)=0.
Теперь докажем, что Р (С)=0. Заметим, что
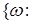    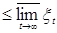 , где , где  и и 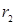 - рациональные числа}= - рациональные числа}= 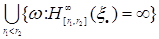 = = 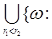  . .
Рассмотрим вероятность Р ( N) в силу неравенства Чебышева и леммы 8 мы имеем: N) в силу неравенства Чебышева и леммы 8 мы имеем:
Р (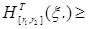 N) N) 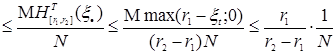 . .
Устремляя теперь  , получаем неравенство , получаем неравенство 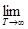 Р ( Р ( N) N) 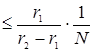 . Отсюда следует, что Р ( . Отсюда следует, что Р (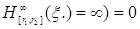 , т.е. Р (С)=0. Доказательство закончено. , т.е. Р (С)=0. Доказательство закончено.
3.3. Определение. Мартингал  называется равномерно интегрируемым, если называется равномерно интегрируемым, если 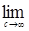  . .
Теорема 9. Пусть  равномерно интегрируемый мартингал, тогда Р -п.н. существует случайная величина равномерно интегрируемый мартингал, тогда Р -п.н. существует случайная величина 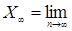 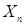 такая, что: такая, что:
а) 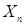 = =  Р - п. н., Р - п. н.,
б)  М | М | 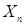 - - 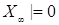 Р - п. н. Р - п. н.
Доказательство этой теоремы следует из теоремы 6.
Дата добавления: 2015-01-18 | Просмотры: 1015 | Нарушение авторских прав
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|

 ,
,  ,
, 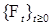 , Р) – стохастический базис, последовательность {
, Р) – стохастический базис, последовательность { 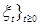 - согласована с потоком
- согласована с потоком  .
. ,
,  ) t > 1 называется мартингалом, если:
) t > 1 называется мартингалом, если:  , 2)
, 2) 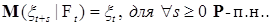
 Р -п. н., то последовательность (
Р -п. н., то последовательность (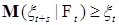 Р - п. н., то последовательность (
Р - п. н., то последовательность ( , где
, где 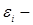 независимые в совокупности случайные величины. Пусть
независимые в совокупности случайные величины. Пусть 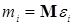 ,
,  . Ясно, что
. Ясно, что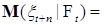

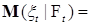
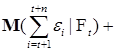
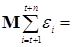
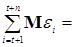
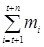 .
. для любого t;
для любого t;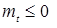 для любого t;
для любого t;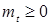 для любого t;
для любого t; ,t,B), то
,t,B), то  t,B) – мартингал для
t,B) – мартингал для 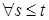 , относительно потока
, относительно потока  алгебр
алгебр  и меры Р.
и меры Р. :
: , t,B)|
, t,B)| 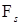 )= M (P (u,
)= M (P (u,  ) =
) = 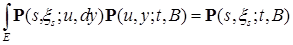 .
.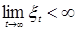 .
.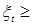 М
М 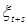 , т.е. в среднем последовательность
, т.е. в среднем последовательность  - убывает. Пусть
- убывает. Пусть  Образуем новую последовательность
Образуем новую последовательность 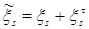 . Понятно, что
. Понятно, что  .Тогда
.Тогда  , значит любой супермартингал представим в виде разности двух неотрицательных супермартингалов.
, значит любой супермартингал представим в виде разности двух неотрицательных супермартингалов.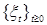 - супермартингал, то
- супермартингал, то 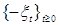 - субмартингал. Поэтому утверждение теоремы 6 верно и для субмартингалов.
- субмартингал. Поэтому утверждение теоремы 6 верно и для субмартингалов. числовая последовательность, a<b, [ a,b ] – отрезок. Обозначим
числовая последовательность, a<b, [ a,b ] – отрезок. Обозначим  - число пересечений отрезка [ a,b ] последовательностью
- число пересечений отрезка [ a,b ] последовательностью 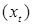 снизу вверх.
снизу вверх. ,
,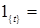
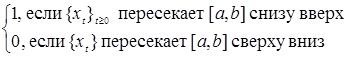
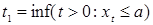 ,
,  ,
, ,
, 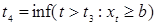 ,
,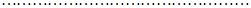
 ,
, 
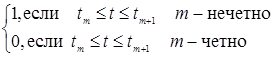
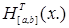 =
= 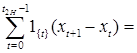
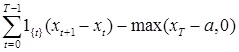 .
.
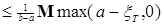 .
.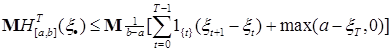 .
.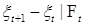 ) ≤ 0. Отсюда следует неравенство
) ≤ 0. Отсюда следует неравенство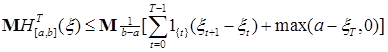

 не существует конечного предела. Через В обозначим множество
не существует конечного предела. Через В обозначим множество 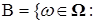
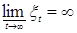 Р - п. н.,
Р - п. н.,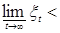
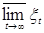 Р - п. н.
Р - п. н.
 }, C =
}, C = 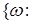

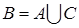 , поэтому
, поэтому  . Значит для доказательства теоремы достаточно доказать, что Р (А) =0 и Р (С)=0.
. Значит для доказательства теоремы достаточно доказать, что Р (А) =0 и Р (С)=0.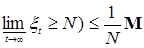

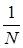
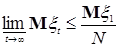 . Устремляя теперь
. Устремляя теперь 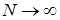 , получаем Р (А)=0.
, получаем Р (А)=0.

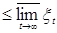 , где
, где  и
и 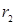 - рациональные числа}=
- рациональные числа}= 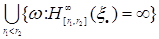 =
= 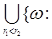
 .
. N) в силу неравенства Чебышева и леммы 8 мы имеем:
N) в силу неравенства Чебышева и леммы 8 мы имеем: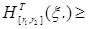 N)
N) 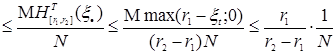 .
. , получаем неравенство
, получаем неравенство 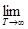 Р (
Р ( N)
N) 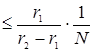 . Отсюда следует, что Р (
. Отсюда следует, что Р (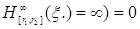 , т.е. Р (С)=0. Доказательство закончено.
, т.е. Р (С)=0. Доказательство закончено. называется равномерно интегрируемым, если
называется равномерно интегрируемым, если 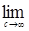
 .
.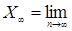
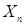 такая, что:
такая, что: Р - п. н.,
Р - п. н., М |
М | 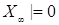 Р - п. н.
Р - п. н.