Существование случайных последовательностей
2.1. Чтобы построить случайную последовательность, надо сконструировать вероятностную меру на его траекториях. Существует два подхода к решению этой проблемы:
1) основанный на переходных вероятностях;
2) основанный на непосредственном задании случайного процесса.
2.2. В данном пункте мы построим марковский процесс (с дискретным временем) с помощью переходных вероятностей. Без ограничения общности, можно считать, что  = ( = ( ). ).
Пусть задано семейство переходных вероятностей { Р (s,  t,B)} и справедливо соотношение Чепмена – Колмогорова. Предположим еще, что задана также вероятностная мера t,B)} и справедливо соотношение Чепмена – Колмогорова. Предположим еще, что задана также вероятностная мера  на на  . Тогда существует вероятностное пространство . Тогда существует вероятностное пространство  и случайная последовательность ( и случайная последовательность ( , ,  ) t > 0 на нем такие, что для любых ) t > 0 на нем такие, что для любых 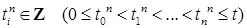 . .
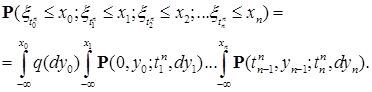
Таким образом определенный марковский процесс ( , ,  ) t > 0 называют марковским процессом с начальным распределением ) t > 0 называют марковским процессом с начальным распределением  и семейством переходных вероятностей { Р (s, и семейством переходных вероятностей { Р (s,  t,B)}. Это построение обобщает следующая теорема о существовании случайной последовательности. t,B)}. Это построение обобщает следующая теорема о существовании случайной последовательности.
Теорема 2. (Ионеску-Тулчи). Пусть  - произвольные измеримые пространства и - произвольные измеримые пространства и  , а , а  . Пусть на ( . Пусть на ( ) задана вероятностная мера Р 1 и для каждого набора ) задана вероятностная мера Р 1 и для каждого набора  на на  заданы вероятностные меры Р заданы вероятностные меры Р  , которые для каждого В , которые для каждого В  являются борелевскими функциями от являются борелевскими функциями от  ), причем для любых ), причем для любых 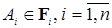
 . .
Тогда на  существуют: 1) единственная вероятностная мера Р такая, что для любого существуют: 1) единственная вероятностная мера Р такая, что для любого 
 (3) (3)
2) случайная последовательность Х =  такая, что такая, что
 (4) (4)
Доказательство этого утверждения читатель может найти в ряде известных руководств [1,3].
Пример: Пусть  ={1,2,…}, Р к (x,y) – семейство неотрицательных функций ={1,2,…}, Р к (x,y) – семейство неотрицательных функций 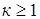 , x,y , x,y  , таких, что , таких, что  Пусть Пусть  распределение вероятностей на распределение вероятностей на 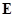 ( (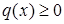  ). Тогда существуют ). Тогда существуют  и семейство случайных величин Х ={ и семейство случайных величин Х ={  на нем таких, что на нем таких, что
P (
В качестве элементов Ω можно взять  . Такая последовательность случайных величин Х ={ . Такая последовательность случайных величин Х ={  называется марковской цепью со счетным множеством состояний называется марковской цепью со счетным множеством состояний 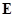 и матрицей переходных вероятностей { Р к (x,y)}, и начальным распределением и матрицей переходных вероятностей { Р к (x,y)}, и начальным распределением 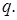
2.3. В данном пункте мы приведем методику непосредственного задания марковской случайной последовательности.
Пусть Ф:  измеримая по Борелю функция, обозначаемая через Ф(t,x,y), где измеримая по Борелю функция, обозначаемая через Ф(t,x,y), где  и и  – полные, сепарабельные, метрические пространства. Последовательность { Xt } t > 0 со значениями – полные, сепарабельные, метрические пространства. Последовательность { Xt } t > 0 со значениями  определим с помощью рекуррентного соотношения определим с помощью рекуррентного соотношения
 , ,  , (5) , (5)
где ( последовательность случайных элементов, принимающая значения в последовательность случайных элементов, принимающая значения в  . Соотношение (5) называется процессом, определенным рекуррентно. Положим, что . Соотношение (5) называется процессом, определенным рекуррентно. Положим, что  - нормированное пространство с нормой - нормированное пространство с нормой  . Возникают два вопроса: . Возникают два вопроса:
1) является ли Xt для любого t 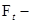 измеримым; измеримым;
2)  | |  Р - п. н. Р - п. н.
Определение. Под сильным решением процесса, определенного рекуррентно, будем понимать последовательность  измеримую относительно измеримую относительно  алгебры алгебры  такую, что: а) Р ( такую, что: а) Р ( | |  )=1; б) она обращает (5) в тождество с вероятностью 1. )=1; б) она обращает (5) в тождество с вероятностью 1.
Определение. Будем говорить, что (5) имеет единственное сильное решение, если из того что существуют  i =1,2 – два сильных решения соотношения (5), причем i =1,2 – два сильных решения соотношения (5), причем  (т.е. они начинаются из одной точки), то Р ( (т.е. они начинаются из одной точки), то Р ( для любого для любого 
Теорема 3. Пусть Ф:  , где , где  – линейное нормированное пространство, удовлетворяющее условиям: – линейное нормированное пространство, удовлетворяющее условиям:
1) ||Ф(t,x,y) – Ф(t,z,y)||  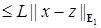
2) ||Ф(t,0,y)||   . .
Тогда: а) если выполнено 1), то решение (5) единственно; б) если выполнены 1) и 2) и Р - п. н.  , то существует сильное решение (5). , то существует сильное решение (5).
Замечание 1. Поясним смысл условий теоремы 3. Очевидны неравенства:
||Ф(t,x,y)||  = ||Ф(t,0,y)+ Ф(t,x,y)- Ф(t, 0, y)|| = ||Ф(t,0,y)+ Ф(t,x,y)- Ф(t, 0, y)||   ||Ф(t, 0, y)|| ||Ф(t, 0, y)||  + ||Ф(t,x,y) - Ф(t, 0, y)|| + ||Ф(t,x,y) - Ф(t, 0, y)||   L + L| | x| | L + L| | x| |  = L (1+|| x || = L (1+|| x ||  ) (т.е. допустим рост по х не быстрее, чем линейный). ) (т.е. допустим рост по х не быстрее, чем линейный).
Доказательство. а) Пусть имеются два сильных решения, начинающихся на одной точке  , имеем Р - п. н. , имеем Р - п. н.
     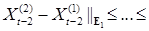
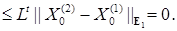
Значит, 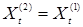 Р - п. н. для Р - п. н. для  . .
б) Заметим,  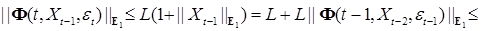
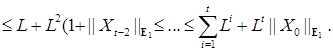
Следовательно, если  Р - п. н. – конечно, то Р - п. н. – конечно, то  Р -п. н. Р -п. н.
Замечания. 1) Пусть  удовлетворяет (5), и удовлетворяет (5), и 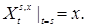 Если (5) имеет единственное сильное решение, то справедливо Р - п. н. Если (5) имеет единственное сильное решение, то справедливо Р - п. н. 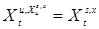 для для 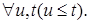
2) Обозначим Р (s,  ,t,B) ,t,B)  = P (t, = P (t,  ,B) – переходную вероятность за один шаг. Из соотношения Чепмена-Колмогорова следует, чтобы построить переходную вероятность за t шагов, достаточно знать переходную вероятность за один шаг. ,B) – переходную вероятность за один шаг. Из соотношения Чепмена-Колмогорова следует, чтобы построить переходную вероятность за t шагов, достаточно знать переходную вероятность за один шаг.
2.4. Установим условия, выполнение которых гарантирует, что процесс, определенный рекуррентно, является марковским.
Теорема 4. Пусть выполняются условия: 1) рекуррентное соотношение (5) имеет единственное сильное решение, 2)  последовательность независимых в совокупности случайных величин (со значениями в последовательность независимых в совокупности случайных величин (со значениями в 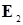 ), 3) ), 3)  не зависит от не зависит от  . Тогда 1) последовательность . Тогда 1) последовательность  - -  -измерима при каждом t и -измерима при каждом t и  - марковская, 2) переходная вероятность за один шаг имеет вид - марковская, 2) переходная вероятность за один шаг имеет вид 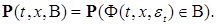
Доказательство. Нам надо доказать, что Р - п. н.
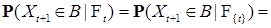  . .
Рассмотрим сначала левую часть этого равенства в силу замечания 1.3.1 Р -п.н.  = =  . .
Так как 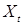 - сильное решение (5), то - сильное решение (5), то 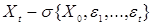 -измеримо, то по теореме Бореля для каждого t существуют функции -измеримо, то по теореме Бореля для каждого t существуют функции  такие, что Р - п. н. такие, что Р - п. н.  . Поэтому, в силу условий 2), 3) имеем Р - п. н. . Поэтому, в силу условий 2), 3) имеем Р - п. н.
 = =  = =  = =
=  = =  . .
Отсюда следует, что 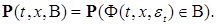 Доказательство закончено. Доказательство закончено.
2.5. Примеры процессов, определенных рекуррентно.
1) Пусть  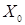 =0, где =0, где  -последовательность независимых (в совокупности) величин. В силу теоремы 4 -последовательность независимых (в совокупности) величин. В силу теоремы 4  является марковской последовательностью. является марковской последовательностью.
2) Дискретная модель диффузии. Рассмотрим рекуррентное соотношение:
  , (6) , (6)
где  - измеримые по Борелю функции, - измеримые по Борелю функции,  - последовательность независимых в совокупности случайных величин, причем - последовательность независимых в совокупности случайных величин, причем 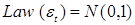 . (6) имеет единственное сильное решение, если выполнены условия: . (6) имеет единственное сильное решение, если выполнены условия:
а) 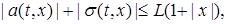
б) 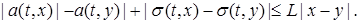
Пусть  , а , а  В этом случае В этом случае 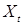 удовлетворяет рекуррентному соотношению удовлетворяет рекуррентному соотношению
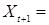  , ,  . (7) . (7)
Покажем, что  , причем , причем
 , ,  ; ;
 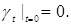
Действительно. Обозначим  , из рекуррентного соотношения (7) следует , из рекуррентного соотношения (7) следует
 М [ М [  ]= ]=  = =  . .
Ясно, что 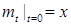 . .
Из определения дисперсии имеем   . Получили рекуррентное соотношение для . Получили рекуррентное соотношение для  . Рассмотрим разность . Рассмотрим разность  , имеем из (7): , имеем из (7):  = =   = = 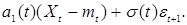
Возведем в квадрат левую и правую части последнего равенства, а затем возьмем математическое ожидание от левой и правой частей, имеем из получившегося равенства:
 = = 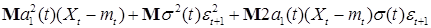
Так как  , то отсюда следует, что , то отсюда следует, что
 . .
Покажем, что  - гауссовская последовательность. Доказательство проведём по индукции. Пусть - гауссовская последовательность. Доказательство проведём по индукции. Пусть 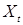 - гауссовская случайная величина. Очевидно, что - гауссовская случайная величина. Очевидно, что  тоже гауссовская. Действительно, так как сумма двух гауссовских величин есть гауссовская величина, то тоже гауссовская. Действительно, так как сумма двух гауссовских величин есть гауссовская величина, то  гауссовская случайная величина. Таким образом основной шаг индукции установлен, а с ним доказано утверждение. гауссовская случайная величина. Таким образом основной шаг индукции установлен, а с ним доказано утверждение.
Дата добавления: 2015-01-18 | Просмотры: 703 | Нарушение авторских прав
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|

 = (
= ( ).
). t,B)} и справедливо соотношение Чепмена – Колмогорова. Предположим еще, что задана также вероятностная мера
t,B)} и справедливо соотношение Чепмена – Колмогорова. Предположим еще, что задана также вероятностная мера  на
на  и случайная последовательность (
и случайная последовательность ( ,
,  ) t > 0 на нем такие, что для любых
) t > 0 на нем такие, что для любых 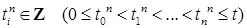 .
.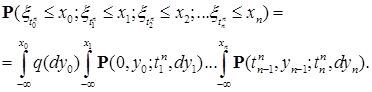
 и семейством переходных вероятностей { Р (s,
и семейством переходных вероятностей { Р (s,  - произвольные измеримые пространства и
- произвольные измеримые пространства и  , а
, а  . Пусть на (
. Пусть на ( ) задана вероятностная мера Р 1 и для каждого набора
) задана вероятностная мера Р 1 и для каждого набора  на
на  заданы вероятностные меры Р
заданы вероятностные меры Р  , которые для каждого В
, которые для каждого В  являются борелевскими функциями от
являются борелевскими функциями от  ), причем для любых
), причем для любых 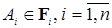
 .
. существуют: 1) единственная вероятностная мера Р такая, что для любого
существуют: 1) единственная вероятностная мера Р такая, что для любого 
 (3)
(3) такая, что
такая, что (4)
(4)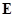 ={1,2,…}, Р к (x,y) – семейство неотрицательных функций
={1,2,…}, Р к (x,y) – семейство неотрицательных функций 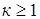 , x,y
, x,y  , таких, что
, таких, что  Пусть
Пусть  распределение вероятностей на
распределение вероятностей на 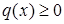
 ). Тогда существуют
). Тогда существуют  на нем таких, что
на нем таких, что
 . Такая последовательность случайных величин Х ={
. Такая последовательность случайных величин Х ={ 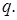
 измеримая по Борелю функция, обозначаемая через Ф(t,x,y), где
измеримая по Борелю функция, обозначаемая через Ф(t,x,y), где  и
и  – полные, сепарабельные, метрические пространства. Последовательность { Xt } t > 0 со значениями
– полные, сепарабельные, метрические пространства. Последовательность { Xt } t > 0 со значениями  ,
,  , (5)
, (5) последовательность случайных элементов, принимающая значения в
последовательность случайных элементов, принимающая значения в  . Соотношение (5) называется процессом, определенным рекуррентно. Положим, что
. Соотношение (5) называется процессом, определенным рекуррентно. Положим, что  - нормированное пространство с нормой
- нормированное пространство с нормой  . Возникают два вопроса:
. Возникают два вопроса: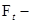 измеримым;
измеримым; |
|  Р - п. н.
Р - п. н. измеримую относительно
измеримую относительно  алгебры
алгебры  такую, что: а) Р (
такую, что: а) Р ( |
|  i =1,2 – два сильных решения соотношения (5), причем
i =1,2 – два сильных решения соотношения (5), причем  (т.е. они начинаются из одной точки), то Р (
(т.е. они начинаются из одной точки), то Р ( для любого
для любого 
 , где
, где 
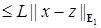
 .
. , то существует сильное решение (5).
, то существует сильное решение (5). ||Ф(t, 0, y)||
||Ф(t, 0, y)|| 




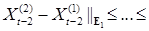
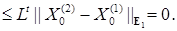
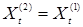 Р - п. н. для
Р - п. н. для  .
.
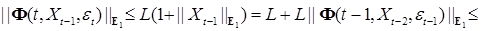
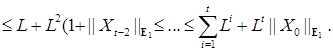
 Р - п. н. – конечно, то
Р - п. н. – конечно, то  Р -п. н.
Р -п. н. удовлетворяет (5), и
удовлетворяет (5), и 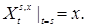 Если (5) имеет единственное сильное решение, то справедливо Р - п. н.
Если (5) имеет единственное сильное решение, то справедливо Р - п. н. 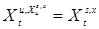 для
для 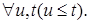
 = P (t,
= P (t,  ,B) – переходную вероятность за один шаг. Из соотношения Чепмена-Колмогорова следует, чтобы построить переходную вероятность за t шагов, достаточно знать переходную вероятность за один шаг.
,B) – переходную вероятность за один шаг. Из соотношения Чепмена-Колмогорова следует, чтобы построить переходную вероятность за t шагов, достаточно знать переходную вероятность за один шаг. последовательность независимых в совокупности случайных величин (со значениями в
последовательность независимых в совокупности случайных величин (со значениями в 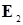 ), 3)
), 3)  не зависит от
не зависит от  . Тогда 1) последовательность
. Тогда 1) последовательность  -
-  -измерима при каждом t и
-измерима при каждом t и  - марковская, 2) переходная вероятность за один шаг имеет вид
- марковская, 2) переходная вероятность за один шаг имеет вид 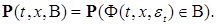
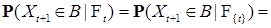
 .
. =
=  .
.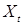 - сильное решение (5), то
- сильное решение (5), то 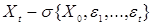 -измеримо, то по теореме Бореля для каждого t существуют функции
-измеримо, то по теореме Бореля для каждого t существуют функции  такие, что Р - п. н.
такие, что Р - п. н.  . Поэтому, в силу условий 2), 3) имеем Р - п. н.
. Поэтому, в силу условий 2), 3) имеем Р - п. н. =
= =
=  .
.
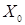 =0, где
=0, где  -последовательность независимых (в совокупности) величин. В силу теоремы 4
-последовательность независимых (в совокупности) величин. В силу теоремы 4 
 , (6)
, (6) - измеримые по Борелю функции,
- измеримые по Борелю функции, 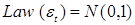 . (6) имеет единственное сильное решение, если выполнены условия:
. (6) имеет единственное сильное решение, если выполнены условия: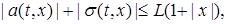
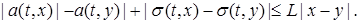
 , а
, а  В этом случае
В этом случае 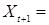
 ,
,  . (7)
. (7) , причем
, причем ,
,  ;
;
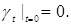
 , из рекуррентного соотношения (7) следует
, из рекуррентного соотношения (7) следует М [
М [  =
=  .
.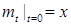 .
. 
 . Получили рекуррентное соотношение для
. Получили рекуррентное соотношение для  . Рассмотрим разность
. Рассмотрим разность  , имеем из (7):
, имеем из (7): 
 =
= 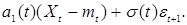
 =
= 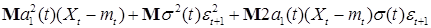
 , то отсюда следует, что
, то отсюда следует, что .
.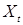 - гауссовская случайная величина. Очевидно, что
- гауссовская случайная величина. Очевидно, что  тоже гауссовская. Действительно, так как сумма двух гауссовских величин есть гауссовская величина, то
тоже гауссовская. Действительно, так как сумма двух гауссовских величин есть гауссовская величина, то