Мартингальные преобразования. Теорема Дуба - Мейера
5.1. Определение. Последовательность  называется предсказуемой, если называется предсказуемой, если  -измеримо при каждом t. -измеримо при каждом t.
Соглашение:  . .
Пусть  - мартингал относительно меры Р. Обозначим - мартингал относительно меры Р. Обозначим
 . .
Определение. Последовательность  , где , где  -предсказуемая последовательность, а -предсказуемая последовательность, а  - мартингал. Такое преобразование называется мартингальным. - мартингал. Такое преобразование называется мартингальным.
Предложение 17. Пусть  ограниченная предсказуемая последовательность, а ограниченная предсказуемая последовательность, а  , где , где  – мартингал относительно меры P, тогда – мартингал относительно меры P, тогда  - мартингал (относительно меры Р). - мартингал (относительно меры Р).
Доказательство. Действительно, очевидна оценка:
 ,так как по условию Р - п.н. ,так как по условию Р - п.н.  для для  ). Отсюда следует, что ). Отсюда следует, что  . (Здесь мы воспользовались тем, что . (Здесь мы воспользовались тем, что  .) .)
Осталось показать Р - п. н.  . Для этого достаточно доказать, что . Для этого достаточно доказать, что 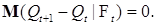 Действительно, для Действительно, для  Р - п.н. имеем Р - п.н. имеем
 . Доказательство закончено. . Доказательство закончено.
5.2. Определение. Последовательность 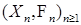 называется обобщенным мартингалом, если для каждого называется обобщенным мартингалом, если для каждого 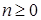 определены условные математические ожидания определены условные математические ожидания  и Р - п. н. и Р - п. н.  . .
Теорема 18. Следующие утверждения эквивалентны:
1) Последовательность 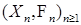 - локальный мартингал. - локальный мартингал.
2) Последовательность 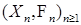 - обобщенный мартингал. - обобщенный мартингал.
3) Последовательность 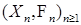 - мартингальное преобразование, т. е. существуют предсказуемая последовательность - мартингальное преобразование, т. е. существуют предсказуемая последовательность  с с 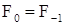 и V0= 0, а также мартингал и V0= 0, а также мартингал  такие, что Р - п. н. Для такие, что Р - п. н. Для 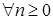

Докажите самостоятельно.
5.3. Для формулировки теоремы Дуба - Мейера нам понадобится следующее определение.
Определение. Последовательность  называется возрастающей, если называется возрастающей, если  Р - п. н. для всех Р - п. н. для всех 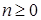 . .
Теорема 19 (Дуба - Мейера). Пусть  - субмартингал, относительно меры Р. Тогда существуют возрастающая предсказуемая последовательность - субмартингал, относительно меры Р. Тогда существуют возрастающая предсказуемая последовательность  и мартингал и мартингал  такие, что Р - п.н. для любого такие, что Р - п.н. для любого 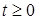
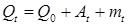 , (8) , (8)
при этом представление (8) Р -п.н. единственно.
Доказательство. Без ограничения общности, можно считать, что  и и  . Образуем две последовательности: . Образуем две последовательности:
 , (9) , (9)
 . (10) . (10)
Складывая (9), (10) получим: 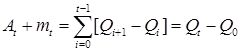 . Нам надо убедиться в том, что . Нам надо убедиться в том, что  - предсказуемый возрастающий процесс, а - предсказуемый возрастающий процесс, а  - мартингал (тем самым мы докажем теорему). - мартингал (тем самым мы докажем теорему).
Рассмотрим последовательность  . По условию . По условию  - субмартингал, следовательно Р - п. н. - субмартингал, следовательно Р - п. н.  , значит , значит  - неубывающая последовательность. Докажем, что - неубывающая последовательность. Докажем, что 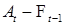 -измеримо (т. е. предсказуема). Ясно, что -измеримо (т. е. предсказуема). Ясно, что 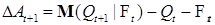 -измеримо, поэтому в силу (10) -измеримо, поэтому в силу (10) 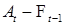 -измеримо. Заметим, что -измеримо. Заметим, что  - мартингал тогда и только тогда, когда - мартингал тогда и только тогда, когда
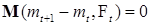 . Из определения . Из определения  следует, что следует, что  Поэтому Поэтому 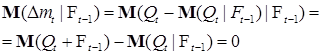
P - п. н..
Предположим, что (8) не единственно, т.е. пусть Р - п. н.
 . .
Поэтому Р - п. н.  . .
Отсюда следует Р - п. н.
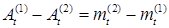 , (11) , (11)
 . (12) . (12)
Вычтем из (11), (12) имеем Р - п. н.
 . (13) . (13)
Возьмем 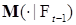 относительно левой и правой частой (13), имеем Р - п.н. относительно левой и правой частой (13), имеем Р - п.н.

Так как  -измеримо, а -измеримо, а  - мартингалы, тогда из последнего равенства следует, что - мартингалы, тогда из последнего равенства следует, что
Р - п.н. для любого t  . По построению . По построению  , поэтому , поэтому  - Р - п. н. для любого t. Следовательно, разложение - Р - п. н. для любого t. Следовательно, разложение  - единственно. Доказательство закончено. - единственно. Доказательство закончено.
Замечание. Пусть  - супермартингал, тогда - супермартингал, тогда 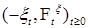 -субмартингал, поэтому -субмартингал, поэтому  , значит , значит  , где , где  - предсказуемый возрастающий процесс, - предсказуемый возрастающий процесс,  - мартингал относительно потока - мартингал относительно потока  и меры Р. и меры Р.
Следствие 20. Пусть  - предсказуемый локальный мартингал. Тогда Р - п. н. - предсказуемый локальный мартингал. Тогда Р - п. н.  .(Докажите самостоятельно). .(Докажите самостоятельно).
5.4. Пример (применения теоремы Дуба - Мейера).
Теорема 21[16]. Пусть  , где , где  - бернуллиевские случайные величины, принимающие значения +1,-1, причем - бернуллиевские случайные величины, принимающие значения +1,-1, причем 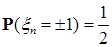 . .
Доказательство. Пусть  -число нулей последовательности -число нулей последовательности  , т.е. , т.е.  Тогда Тогда 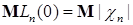 . В силу теоремы Дуба - Мейера имеем . В силу теоремы Дуба - Мейера имеем  . Заметим, что . Заметим, что
 . .
В силу марковского свойства последовательности 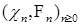 , имеем Р -п.н. , имеем Р -п.н.
 Таким образом Таким образом  , поэтому Р -п.н. , поэтому Р -п.н.
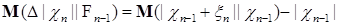 . .
Рассмотрим множество  . Заметим, что Р -п.н.: а) при . Заметим, что Р -п.н.: а) при 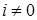
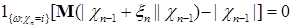 , б) , б)  . Поэтому . Поэтому 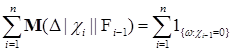 Р -п.н. Р -п.н.
Очевидно, что  -число попаданий в точку нуль последовательностью -число попаданий в точку нуль последовательностью 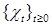 за время N. Тогда за время N. Тогда  Р - п. н. Из последнего равенства следует, что Р - п. н. Из последнего равенства следует, что 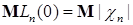 . Доказательство закончено. . Доказательство закончено.
Замечание.  - среднее число нулей последовательности - среднее число нулей последовательности  в симметричном случайном блуждании. в симметричном случайном блуждании.
Заметим, что  при при 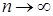 . Значит . Значит  , следовательно , следовательно  - среднее число нулей в симметричном случайном блуждании. - среднее число нулей в симметричном случайном блуждании.
Дата добавления: 2015-01-18 | Просмотры: 1372 | Нарушение авторских прав
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|

 называется предсказуемой, если
называется предсказуемой, если  -измеримо при каждом t.
-измеримо при каждом t. .
. - мартингал относительно меры Р. Обозначим
- мартингал относительно меры Р. Обозначим  .
. , где
, где  -предсказуемая последовательность, а
-предсказуемая последовательность, а  ограниченная предсказуемая последовательность, а
ограниченная предсказуемая последовательность, а  - мартингал (относительно меры Р).
- мартингал (относительно меры Р). ,так как по условию Р - п.н.
,так как по условию Р - п.н.  для
для  ). Отсюда следует, что
). Отсюда следует, что  . (Здесь мы воспользовались тем, что
. (Здесь мы воспользовались тем, что  .)
.) . Для этого достаточно доказать, что
. Для этого достаточно доказать, что 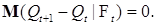 Действительно, для
Действительно, для  Р - п.н. имеем
Р - п.н. имеем . Доказательство закончено.
. Доказательство закончено.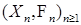 называется обобщенным мартингалом, если для каждого
называется обобщенным мартингалом, если для каждого 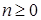 определены условные математические ожидания
определены условные математические ожидания  и Р - п. н.
и Р - п. н.  .
. с
с 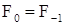 и V0= 0, а также мартингал
и V0= 0, а также мартингал 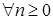

 называется возрастающей, если
называется возрастающей, если  Р - п. н. для всех
Р - п. н. для всех  и мартингал
и мартингал  такие, что Р - п.н. для любого
такие, что Р - п.н. для любого 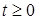
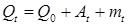 , (8)
, (8) и
и  . Образуем две последовательности:
. Образуем две последовательности: , (9)
, (9) . (10)
. (10)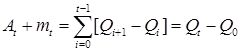 . Нам надо убедиться в том, что
. Нам надо убедиться в том, что  - мартингал (тем самым мы докажем теорему).
- мартингал (тем самым мы докажем теорему). . По условию
. По условию  - субмартингал, следовательно Р - п. н.
- субмартингал, следовательно Р - п. н.  , значит
, значит 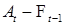 -измеримо (т. е. предсказуема). Ясно, что
-измеримо (т. е. предсказуема). Ясно, что 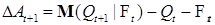 -измеримо, поэтому в силу (10)
-измеримо, поэтому в силу (10) 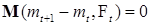 . Из определения
. Из определения  следует, что
следует, что  Поэтому
Поэтому 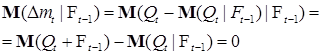
 .
. .
.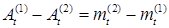 , (11)
, (11) . (12)
. (12) . (13)
. (13)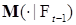 относительно левой и правой частой (13), имеем Р - п.н.
относительно левой и правой частой (13), имеем Р - п.н.
 -измеримо, а
-измеримо, а  - мартингалы, тогда из последнего равенства следует, что
- мартингалы, тогда из последнего равенства следует, что . По построению
. По построению  , поэтому
, поэтому  - Р - п. н. для любого t. Следовательно, разложение
- Р - п. н. для любого t. Следовательно, разложение  - единственно. Доказательство закончено.
- единственно. Доказательство закончено.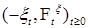 -субмартингал, поэтому
-субмартингал, поэтому  , значит
, значит  , где
, где  - мартингал относительно потока
- мартингал относительно потока  и меры Р.
и меры Р. - предсказуемый локальный мартингал. Тогда Р - п. н.
- предсказуемый локальный мартингал. Тогда Р - п. н.  .(Докажите самостоятельно).
.(Докажите самостоятельно). , где
, где  - бернуллиевские случайные величины, принимающие значения +1,-1, причем
- бернуллиевские случайные величины, принимающие значения +1,-1, причем 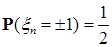 .
. -число нулей последовательности
-число нулей последовательности  , т.е.
, т.е.  Тогда
Тогда 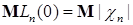 . В силу теоремы Дуба - Мейера имеем
. В силу теоремы Дуба - Мейера имеем  . Заметим, что
. Заметим, что  .
.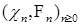 , имеем Р -п.н.
, имеем Р -п.н. Таким образом
Таким образом  , поэтому Р -п.н.
, поэтому Р -п.н.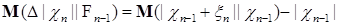 .
. . Заметим, что Р -п.н.: а) при
. Заметим, что Р -п.н.: а) при 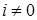
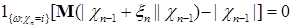 , б)
, б)  . Поэтому
. Поэтому 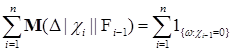 Р -п.н.
Р -п.н. -число попаданий в точку нуль последовательностью
-число попаданий в точку нуль последовательностью 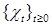 за время N. Тогда
за время N. Тогда  Р - п. н. Из последнего равенства следует, что
Р - п. н. Из последнего равенства следует, что  - среднее число нулей последовательности
- среднее число нулей последовательности  в симметричном случайном блуждании.
в симметричном случайном блуждании. при
при 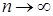 . Значит
. Значит  , следовательно
, следовательно  - среднее число нулей в симметричном случайном блуждании.
- среднее число нулей в симметричном случайном блуждании.