Теорема 1. Винеровский процесс существует
Доказательство теоремы опирается на два вспомогательных утверждения
1.1.1. Лемма 2. Пусть 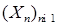 последовательность гауссовских случайных величин такая, что существует последовательность гауссовских случайных величин такая, что существует 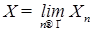 .Тогда X -гауссовская случайная величина. .Тогда X -гауссовская случайная величина.
Доказательство. Обозначим 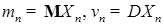 . Тогда, в силу свойства гауссовости последовательности . Тогда, в силу свойства гауссовости последовательности 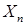 , имеем , имеем 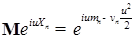 Пусть любые Пусть любые  ,а ,а 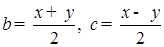 , тогда имеем , тогда имеем
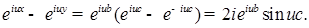
Отсюда следует, что 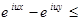 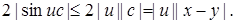
Поэтому 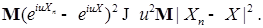
Значит, 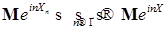 , так как , так как 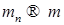 и и 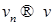 , при , при 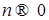 т.е. т.е.
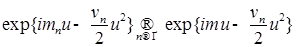 . Доказательство закончено. . Доказательство закончено.
1.1.2. Лемма 3. Пусть 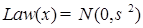 . Пусть . Пусть 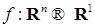 , , 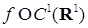 , причем , причем 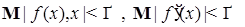 . Тогда справедливо равенство . Тогда справедливо равенство 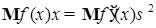 . .
Доказательство утверждения леммы следует из формулы интегрирования по частям.
1.1.3. Доказательство (теоремы 1) Пусть 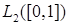 - пространство измеримых квадратично интегрируемых относительно меры Лебега функций, заданных на отрезке [0,1] со значениями в - пространство измеримых квадратично интегрируемых относительно меры Лебега функций, заданных на отрезке [0,1] со значениями в 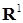 . Пусть . Пусть 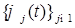 - ортонормированное семейство функций в - ортонормированное семейство функций в 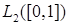 , т.е. , т.е. 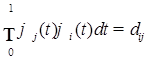 , где , где 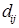 - символ Кронекера. Обозначим - символ Кронекера. Обозначим 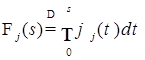 . Пусть . Пусть 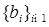 – счетное семейство независимых в совокупности стандартных нормальных случайных величин. Для доказательства теоремы достаточно доказать, что ряд – счетное семейство независимых в совокупности стандартных нормальных случайных величин. Для доказательства теоремы достаточно доказать, что ряд 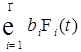 P - п. н. cходится для любого t и обладает свойствами i)-iv). P - п. н. cходится для любого t и обладает свойствами i)-iv).
Пусть 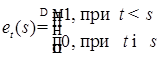 . Очевидно, что: . Очевидно, что:
1) 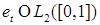 ; ;
2) 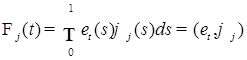 , где , где 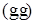 - скалярное произведение в - скалярное произведение в
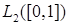 ; ;
3) 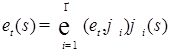 ; ;
4) 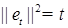 , где , где 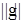 - норма в - норма в 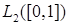 . .
Обозначим 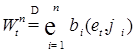 . Очевидно, что: . Очевидно, что:
1) для любого 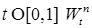 - гауссовская случайная величина, причем для любых n; - гауссовская случайная величина, причем для любых n;
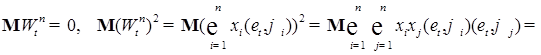 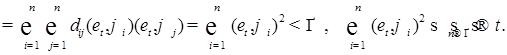 (1) (1)
Отсюда следует, что 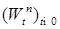 - квадратично интегрируем. Рассмотрим - квадратично интегрируем. Рассмотрим 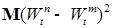 , причем без ограничения общности можно считать, что , причем без ограничения общности можно считать, что 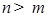 . В силу (1), имеем . В силу (1), имеем
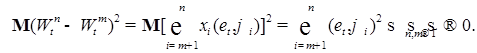
Стало быть, справедлив критерий Коши. Поэтому 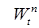 в среднеквадратичном смысле сходится к некоторой в среднеквадратичном смысле сходится к некоторой 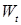 , т.е. , т.е. 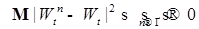 для любого для любого 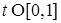 , причем в силу леммы 2 случайная величина , причем в силу леммы 2 случайная величина 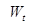 имеет гауссовское распределение. имеет гауссовское распределение.
Построенный процесс обладает свойствами.
1) 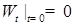 ; ;
1) Траектории 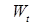 - непрерывны. - непрерывны.
Действительно, в силу леммы 3 имеем 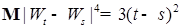 , отсюда в силу теоремы 2 главы 3 получаем утверждение. , отсюда в силу теоремы 2 главы 3 получаем утверждение.
1) 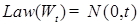 (следует из леммы 2). (следует из леммы 2).
Осталось установить, что 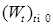 – процесс с независимыми приращениями. Для этого достаточно показать, что – процесс с независимыми приращениями. Для этого достаточно показать, что 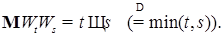 Действительно, Действительно, 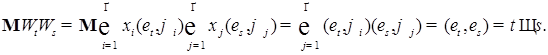
Доказательство закончено.
1.1.4. Замечания. 1) Рассмотрим 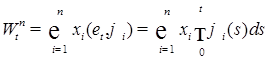 . Отсюда следует, что . Отсюда следует, что 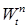 для любого для любого 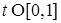 и ограниченного n дифференцируем по t, т.е. P - п. н. существует и ограниченного n дифференцируем по t, т.е. P - п. н. существует 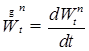 , причем , причем 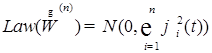 . Очевидно, что . Очевидно, что 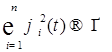 при при  для любого для любого 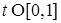 . .
2) Из неравенства Коши-Буняковского следует, что 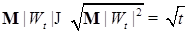 . .
1.2. Теорема 4. Обозначим 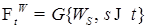 . Тогда относительно меры Р . Тогда относительно меры Р 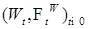 винеровский процесс является мартингалом. винеровский процесс является мартингалом.
Доказательство. Нам надо проверить: 1) 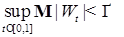 ; 2) ; 2) 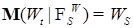 при при 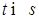 . Заметим, что 1) следует из пункта 2) замечания 1.1.4. Осталось доказать, что . Заметим, что 1) следует из пункта 2) замечания 1.1.4. Осталось доказать, что 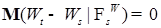 , но в силу того, что , но в силу того, что 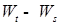 имеет независимые приращения имеем имеет независимые приращения имеем 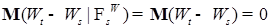 . .
Доказательство закончено.
1.2.1. Замечание. Очевидно, что 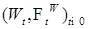 является квадратично интегрируемым мартингалом относительно меры Р. является квадратично интегрируемым мартингалом относительно меры Р.
1.3. В дальнейшем нам понадобится одно свойство приращений винеровского процесса.
Теорема 5. Пусть  и. Пусть и. Пусть 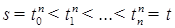 разбиение отрезка [ s,t ] такое, что разбиение отрезка [ s,t ] такое, что 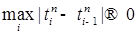 , когда , когда  . .
Тогда 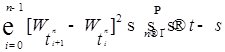 . .
Дата добавления: 2015-01-18 | Просмотры: 967 | Нарушение авторских прав
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|

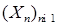 последовательность гауссовских случайных величин такая, что существует
последовательность гауссовских случайных величин такая, что существует 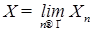 .Тогда X -гауссовская случайная величина.
.Тогда X -гауссовская случайная величина.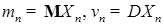 . Тогда, в силу свойства гауссовости последовательности
. Тогда, в силу свойства гауссовости последовательности 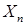 , имеем
, имеем 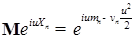 Пусть любые
Пусть любые  ,а
,а 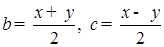 , тогда имеем
, тогда имеем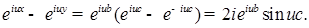
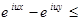
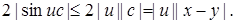
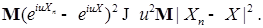
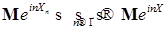 , так как
, так как 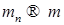 и
и 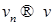 , при
, при 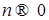 т.е.
т.е.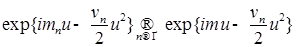 . Доказательство закончено.
. Доказательство закончено.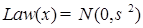 . Пусть
. Пусть 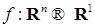 ,
, 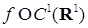 , причем
, причем 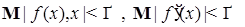 . Тогда справедливо равенство
. Тогда справедливо равенство 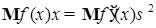 .
.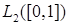 - пространство измеримых квадратично интегрируемых относительно меры Лебега функций, заданных на отрезке [0,1] со значениями в
- пространство измеримых квадратично интегрируемых относительно меры Лебега функций, заданных на отрезке [0,1] со значениями в 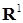 . Пусть
. Пусть 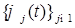 - ортонормированное семейство функций в
- ортонормированное семейство функций в 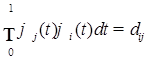 , где
, где 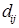 - символ Кронекера. Обозначим
- символ Кронекера. Обозначим 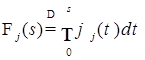 . Пусть
. Пусть 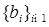 – счетное семейство независимых в совокупности стандартных нормальных случайных величин. Для доказательства теоремы достаточно доказать, что ряд
– счетное семейство независимых в совокупности стандартных нормальных случайных величин. Для доказательства теоремы достаточно доказать, что ряд 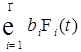 P - п. н. cходится для любого t и обладает свойствами i)-iv).
P - п. н. cходится для любого t и обладает свойствами i)-iv).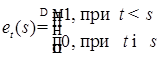 . Очевидно, что:
. Очевидно, что: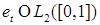 ;
;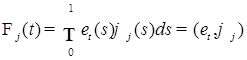 , где
, где 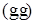 - скалярное произведение в
- скалярное произведение в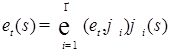 ;
;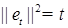 , где
, где 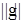 - норма в
- норма в 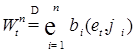 . Очевидно, что:
. Очевидно, что: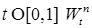 - гауссовская случайная величина, причем для любых n;
- гауссовская случайная величина, причем для любых n;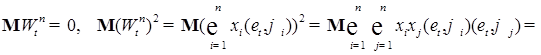
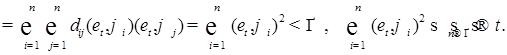 (1)
(1)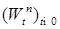 - квадратично интегрируем. Рассмотрим
- квадратично интегрируем. Рассмотрим 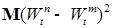 , причем без ограничения общности можно считать, что
, причем без ограничения общности можно считать, что 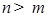 . В силу (1), имеем
. В силу (1), имеем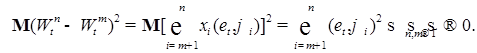
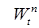 в среднеквадратичном смысле сходится к некоторой
в среднеквадратичном смысле сходится к некоторой 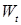 , т.е.
, т.е. 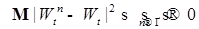 для любого
для любого 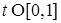 , причем в силу леммы 2 случайная величина
, причем в силу леммы 2 случайная величина 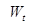 имеет гауссовское распределение.
имеет гауссовское распределение.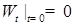 ;
;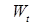 - непрерывны.
- непрерывны.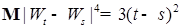 , отсюда в силу теоремы 2 главы 3 получаем утверждение.
, отсюда в силу теоремы 2 главы 3 получаем утверждение.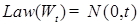 (следует из леммы 2).
(следует из леммы 2).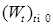 – процесс с независимыми приращениями. Для этого достаточно показать, что
– процесс с независимыми приращениями. Для этого достаточно показать, что 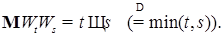 Действительно,
Действительно, 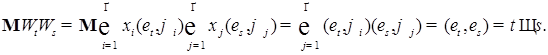
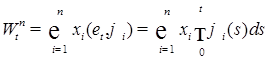 . Отсюда следует, что
. Отсюда следует, что 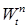 для любого
для любого 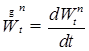 , причем
, причем 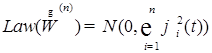 . Очевидно, что
. Очевидно, что 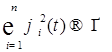 при
при  для любого
для любого 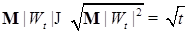 .
.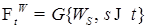 . Тогда относительно меры Р
. Тогда относительно меры Р 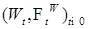 винеровский процесс является мартингалом.
винеровский процесс является мартингалом.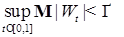 ; 2)
; 2) 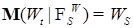 при
при 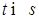 . Заметим, что 1) следует из пункта 2) замечания 1.1.4. Осталось доказать, что
. Заметим, что 1) следует из пункта 2) замечания 1.1.4. Осталось доказать, что 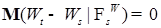 , но в силу того, что
, но в силу того, что 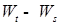 имеет независимые приращения имеем
имеет независимые приращения имеем 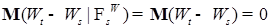 .
. и. Пусть
и. Пусть 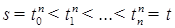 разбиение отрезка [ s,t ] такое, что
разбиение отрезка [ s,t ] такое, что 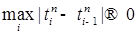 , когда
, когда 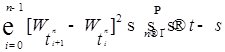 .
.