 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Уравнения Колмогорова8.1. В данном параграфе мы установим связь между стохастическими уравнениями и задачей Коши для уравнений в частных производных второго порядка параболического типа, которые соответствуют прямому и обратному уравнениям Колмогорова. 8.2. В данном пункте мы выведем обратное уравнение Колмогорова. Через Теорема 20. Пусть
Лемма 21. Пусть
где Тогда Р -п. н. Доказательство. Без ограничения общности можно считать, что Р -п. н. Очевидно, что то Но 8.2.2. Доказательство теоремы 20. Так как
В силу условий теоремы и непрерывности процесса 8.3. В данном пункте мы выведем прямое уравнение Колмогорова, соответствующее стохастическому уравнению (22). Теорема 22. Пусть выполнены условия теоремы 19. Пусть для любого
8.3.2. Доказательство теоремы 22. Пусть
Возьмем математическое ожидание относительно левой и правой частей (46), учитывая свойства стохастических интегралов, имеем
В силу условий теоремы и теоремы Фубини последнее равенство можно переписать в виде
Положим
Отсюда, в силу произвольности функции Литература. 1. А.Н.Ширяев. Вероятность. М.: Наука, 1980, 576с. 2. А.Д.Вентцель. Курс теории случайных процессов. М.: Наука, 1996, 399с. 3. Ж.Невё. Математические основания теории вероятностей. М.: Мир, 1969, 309с. 4. И.И.Гихман, Н.В.Скороход. Теория случайных процессов, т.2. М.: Наука, 1973, 639с. 5. Е.Б.Дынкин. Марковские процессы. М.: Физматиз, 1963, 859с. 6. Р.Ш.Липцер, А.Н.Ширяев. Статистика случайных процессов. М.: Наука, 1974, 696с. 7. Р.Ш.Липцер, А.Н.Ширяев. Теория мартингалов. М.: Наука, 1986, 512с. 8. Ж.Жакод, А.Н.Ширяев. Предельные теоремы для случайных процессов, т1. М.: Физ-мат. лит., 1994, 542с. 9. Р.А.Мейер. Вероятность и потенциалы. М.: Мир, 1973, 324с. 10. Дж.Дуб. Вероятностные процессы. М.: ИЛ, 1956, 605с. 11. П.Халмош. Теория меры М.: ИЛ, 1953, 291с. 12. П.Биллингсли. Сходимость вероятностных мер. М.: Наука, 1977, 351с. 13. А.Н. Колмогоров, С.В.Фомин. Элементы теории функций и функционального анализа. М.: Наука, 1989, 496с. 14. P.Bremand. Point Processes and Queunes (Martingale Dynamics). Springer-Verlag, New York-Heideberg-Berlin, 1981, 354p. 15. Н.Н.Лебедев. Специальные функции и их приложения. М.: Физ-мат. лит., 1963, 358с. 16. А.В.Булинский, А.Н.Ширяев. Теория случайных процессов. М.: Физ-мат. лит., 2003, 400с. 17. Б.Оксендаль. Стохастические дифференциальные уравнения. Введение в теорию и приложения. М.: Мир, 2003, 408с. Список обозначений.
! - единственный
Дата добавления: 2015-01-18 | Просмотры: 973 | Нарушение авторских прав |
 обозначим пространство функций, определённых на
обозначим пространство функций, определённых на  , со значениями в
, со значениями в 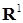 , один раз дифференцируемых по
, один раз дифференцируемых по  и два раза по
и два раза по  , причём эти производные непрерывны и ограничены.
, причём эти производные непрерывны и ограничены. - единственное сильное решение стохастического уравнения (22), коэффициенты которого непрерывны по совокупности переменных. Пусть
- единственное сильное решение стохастического уравнения (22), коэффициенты которого непрерывны по совокупности переменных. Пусть  ,
,  , причём
, причём  . Тогда
. Тогда  удовлетворяет уравнению
удовлетворяет уравнению (41)
(41) - квадратично интегрируемый мартингал, допускающий представление
- квадратично интегрируемый мартингал, допускающий представление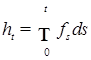 , (42)
, (42) – неупреждающий процесс такой, что Р -п. н.
– неупреждающий процесс такой, что Р -п. н.  .
.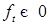 .
. . Пусть
. Пусть  - разбиение отрезка
- разбиение отрезка  такое, что
такое, что  .
. . Так как
. Так как 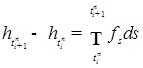 ,
,
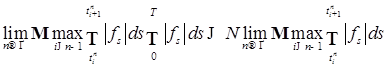 .
. Р -п. н. и при
Р -п. н. и при  Р -п. н.
Р -п. н.  . Следовательно
. Следовательно  . Доказательство закончено.
. Доказательство закончено. удовлетворяет стохастическому уравнению (36), а
удовлетворяет стохастическому уравнению (36), а  , то к
, то к  можно применить формулу Ито, имеем
можно применить формулу Ито, имеем (43)
(43)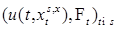 является мартингалом относительно меры Р. Кроме того, стохастический интеграл
является мартингалом относительно меры Р. Кроме того, стохастический интеграл  является мартингалом относительно меры Р. Поэтому мартингалом относительно потока
является мартингалом относительно меры Р. Поэтому мартингалом относительно потока  и меры Р является второе слагаемое правой части (43). Следовательно, в силу леммы 21 Р -п. н.
и меры Р является второе слагаемое правой части (43). Следовательно, в силу леммы 21 Р -п. н. . (44)
. (44) по
по 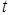 можно осуществить предельный переход равенстве (44) при
можно осуществить предельный переход равенстве (44) при  . В результате уравнение (41). Осталось отметить, что
. В результате уравнение (41). Осталось отметить, что  . Доказательство закончено.
. Доказательство закончено. существует плотность распределения
существует плотность распределения  , обозначаемая через
, обозначаемая через  . Кроме того, пусть существуют производные
. Кроме того, пусть существуют производные  ,
,  ,
,  для любых
для любых  . Тогда плотность распределения
. Тогда плотность распределения  (45)
(45) - бесконечно дифференцируемая функция с компактным носителем [13], а
- бесконечно дифференцируемая функция с компактным носителем [13], а  (46)
(46) .
.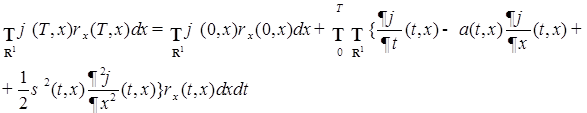
 для любого х. Кроме того, в силу формулы интегрирования по частям правая часть последнего равенства будет иметь вид (в силу свойств функции
для любого х. Кроме того, в силу формулы интегрирования по частям правая часть последнего равенства будет иметь вид (в силу свойств функции  )
) .
. - принадлежит
- принадлежит - пересечение
- пересечение - объединение
- объединение - дополнение
- дополнение - включение
- включение - пустое множество
- пустое множество - любой
- любой - существует
- существует - по определению
- по определению - градиент
- градиент - сумма
- сумма - произведение
- произведение
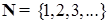
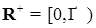
 - n- мерное евклидово пространство
- n- мерное евклидово пространство - польское (полное метрическое сепарабельное) пространство
- польское (полное метрическое сепарабельное) пространство - σ-алгебра борелевских множеств на
- σ-алгебра борелевских множеств на 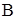
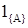 - индикатор множества А
- индикатор множества А - декартово произведение множеств X и Y
- декартово произведение множеств X и Y - σ-алгебра, равная произведению σ-алгебр
- σ-алгебра, равная произведению σ-алгебр  и
и  - точная верхняя (нижняя) грань
- точная верхняя (нижняя) грань - предел
- предел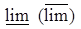 - нижний (верхний) предел
- нижний (верхний) предел - монотонно стремиться снизу (сверху)
- монотонно стремиться снизу (сверху) - знак для различных видов сходимости
- знак для различных видов сходимости - отображение
- отображение 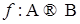
 - пространство непрерывных ограниченных функций на Е со значениями в
- пространство непрерывных ограниченных функций на Е со значениями в  - пространство измеримых ограниченных функций на Е со значениями в
- пространство измеримых ограниченных функций на Е со значениями в  - норма
- норма