 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Поэтому для доказательства теоремы достаточно показать, что
Действительно, в силу теоремы Фубини, имеем:
Заметим, что в силу леммы 3
Значит, (2) с учетом (3) будет иметь вид:
1.1 Свойства винеровского процесса. 1) Пусть 2) Свойство автомодальности: для любого 3) Достаточно показать, что 4) P – п. н. Это утверждение следует из того, что 5) Процесс 6) Неравенство Дуба. Для любого
Доказательство. Пусть Поэтому Из равенства
8) Гёльдеровское свойство Леви
Доказательство этого утверждения проведем в два этапа: 1) сначала покажем, что P - п. н.
1) Доказательство неравенства
Обозначим Так как
2) Установим неравенство
Так как Замечание. Из гёльдеровского свойства Леви следует, что P - п. н. Дата добавления: 2015-01-18 | Просмотры: 695 | Нарушение авторских прав |
 .
.
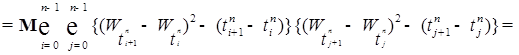
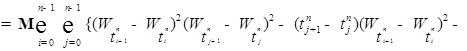
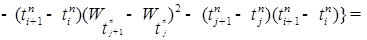
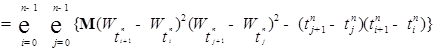 . (2)
. (2) (3)
(3) Доказательство закончено.
Доказательство закончено. - винеровский процесс, не зависящий от
- винеровский процесс, не зависящий от 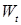 . (Докажите самостоятельно).
. (Докажите самостоятельно). процесс
процесс  , является винеровским процессом. Достаточно показать, что
, является винеровским процессом. Достаточно показать, что  . Действительно
. Действительно  .
. для любого
для любого 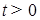 – винеровский процесс.
– винеровский процесс. . Действительно,
. Действительно,  .
.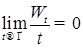 .
. и усиленного закона больших чисел.
и усиленного закона больших чисел.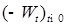 является винеровским процессом,
является винеровским процессом, Это равенство следует из леммы 3.
Это равенство следует из леммы 3.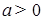
 (4)
(4) . Очевидно, что
. Очевидно, что  (докажите это неравенство самостоятельно). Заметим, что
(докажите это неравенство самостоятельно). Заметим, что 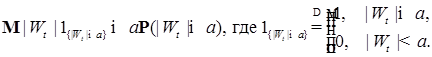
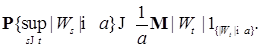 (5)
(5) P – п. н. и неравенства Иенсена
P – п. н. и неравенства Иенсена получаем, что
получаем, что Из (5) и приведенных неравенств следует неравенство Дуба.
Из (5) и приведенных неравенств следует неравенство Дуба. .
. , 2) установим неравенство
, 2) установим неравенство P – п. н.
P – п. н. и
и 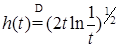 . Пусть имеется диадическое разбиение отрезка [0, t ] точками
. Пусть имеется диадическое разбиение отрезка [0, t ] точками  . Тогда имеем
. Тогда имеем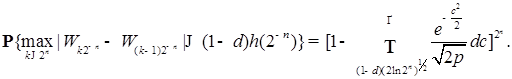
 . Значит, справедливо неравенство
. Значит, справедливо неравенство 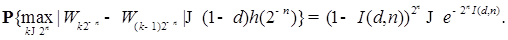
 Поэтому, в силу леммы Бореля-Кантелли, имеем при
Поэтому, в силу леммы Бореля-Кантелли, имеем при 
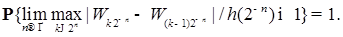
 . Тогда имеем
. Тогда имеем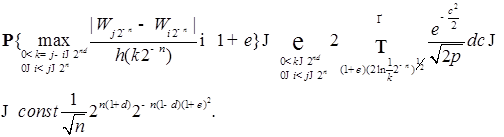
 , то правая часть последнего неравенства является общим членом сходящегося ряда. Следовательно, в силу леммы Бореля-Кантелли получаем утверждение.
, то правая часть последнего неравенства является общим членом сходящегося ряда. Следовательно, в силу леммы Бореля-Кантелли получаем утверждение.