 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Существование и единственность сильных решений стохастических уравнений5.1. В данном параграфе мы вводим понятия стохастического дифференциального уравнения, а также устанавливаем условия разрешимости этих уравнений. 5.2. Пусть имеется стохастический базис Определение. Будем говорить, что случайный процесс Ито
если В дальнейшем (22) будем называть стохастическим уравнением. Определение. Будем говорить, что стохастическое уравнение (22) имеет единственное сильное решение, если для любых его двух сильных решений 5.3. Приведём, а затем и обоснуем условия существования и единственности сильных решений стохастического уравнения (22). Теорема 12. Пусть выполняются условия: 1) 2) существует константа i) ii) 3) случайная величина Тогда у стохастического уравнения (22) существует единственное сильное решение для любого Замечание. Из условия 2) теоремы следует, что коэффициенты стохастического уравнения (22) удовлетворяют условию
Доказательство. Установим сначала единственность сильного решения стохастического уравнения (22). Пусть
Возьмём математическое ожидание относительно левой и правой частей неравенства (22), а затем к первому слагаемому правой части (22 применим неравенство Коши-Буняковского, имеем
Из свойств стохастических интегралов, условия 2) теоремы и теоремы Фубини, имеем из (22)
Отсюда, в силу леммы Гронуолла-Беллмана, следует единственность сильного решения у (22). Установим, теперь, существование сильного решения у (22). Для этого воспользуемся методом последовательных приближений. Положим
Сначала покажем, что для любых
Отсюда, в силу леммы 9 и условия 2i), имеем
Поэтому ряд
Стало быть, в силу леммы Бореля-Кантелли ряд
Покажем, что построенный процесс является решением уравнения (22). В соответствии с (25), покажем, что равномерно по t
Заметим, что: i) в силу условия Липшица, Р -п. н. имеем
ii) в силу леммы 10 и условия Липшица, имеем для любых
Так как 5.4. Замечание. Пусть
Из теоремы 12 следует, что существует функционал
Тогда очевидно следующее равенство Р-п. н. для любого
Дата добавления: 2015-01-18 | Просмотры: 663 | Нарушение авторских прав |
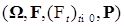 и
и  - винеровский процесс на нём. Через
- винеровский процесс на нём. Через  обозначим измеримое пространство непрерывных функций
обозначим измеримое пространство непрерывных функций 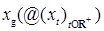 на
на  со значениями в
со значениями в 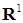 . Пусть
. Пусть  - измеримые функции.
- измеримые функции.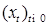 является сильным решением стохастического уравнения
является сильным решением стохастического уравнения , (22),
, (22), и при каждом
и при каждом 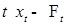 - измерим,
- измерим, 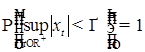 и Р -п. н. справедливо (22).
и Р -п. н. справедливо (22). , таких, что
, таких, что  , справедливо
, справедливо  .
. ,
, 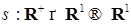 – измеримые функции;
– измеримые функции; такая, что для любых
такая, что для любых  :
: ,
,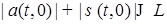 ;
;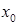 не зависит от
не зависит от 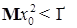 .
. .
.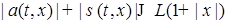 . Действительно, из условия 2) следует, что
. Действительно, из условия 2) следует, что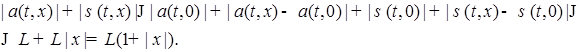
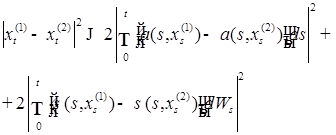 (23)
(23)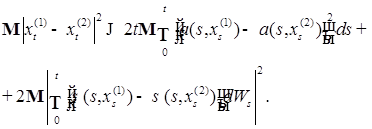 (24)
(24)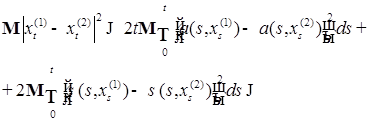
 .
.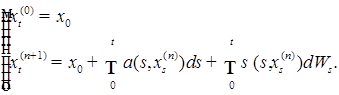 (25).
(25).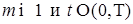 существует константа
существует константа 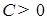 такая, что
такая, что 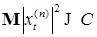 . Действительно, из (25), в силу замечания из пункта 5.3.1, имеем
. Действительно, из (25), в силу замечания из пункта 5.3.1, имеем . (26)
. (26)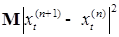 . В силу (25) и условия Липшица, имеем
. В силу (25) и условия Липшица, имеем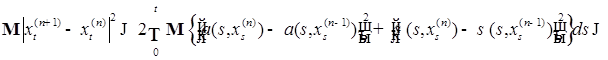
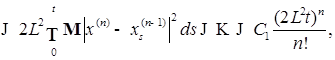 (27)
(27)  . Заметим теперь, что Р -п. н.
. Заметим теперь, что Р -п. н.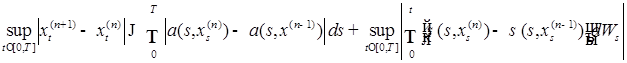
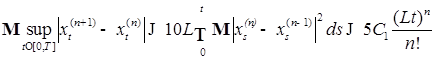 .
.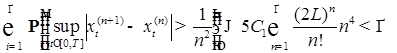 .
.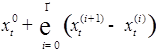 сходится Р -п. н. равномерно по t. Значит последовательность непрерывных процессов
сходится Р -п. н. равномерно по t. Значит последовательность непрерывных процессов  Р -п. н. равномерно сходится к непрерывному процессу
Р -п. н. равномерно сходится к непрерывному процессу 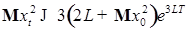 .
. при
при  . Из (23) и (25) имеем Р -п. н.
. Из (23) и (25) имеем Р -п. н. . (28).
. (28).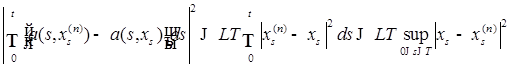 , (29).
, (29).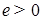 и
и 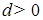
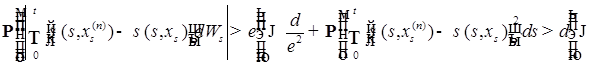
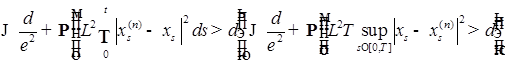 . (30).
. (30). , поэтому из (30) и (29) следует, что (28) стремится к 0 по вероятности при
, поэтому из (30) и (29) следует, что (28) стремится к 0 по вероятности при  является сильным решением, так как из предыдущих построений следует, что оно
является сильным решением, так как из предыдущих построений следует, что оно 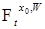 - измеримо, где
- измеримо, где 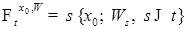 . Доказательство закончено.
. Доказательство закончено.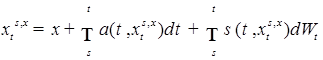 . (31).
. (31). , где
, где  - пространство непрерывных функций на
- пространство непрерывных функций на  со значениями в
со значениями в 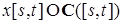 , обозначаемый через
, обозначаемый через 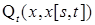 такой, что Р -п. н.
такой, что Р -п. н. 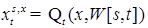 . Пусть
. Пусть 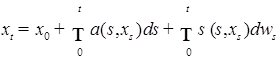 .
.
 .
.