 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Замечание. Неупреждающие функции часто называют функциями, не зависящими от будущего2.3. Определение. Функция случайные величины
Для простых функций
и, так как
Для стохастического интеграла от простой функции Очевидно, что
где Отметим, теперь основные свойства стохастических интегралов от простых функций: 1) 2) 3) 4) 5) Действительно, так как
Рассмотрим первую сумму правой части равенства (9), в силу свойства K* условного математического ожидания (смотри §12 главы 1) и свойства iii) винеровского процесса, имеем
Поэтому, имеем
Рассмотрим вторую сумму правой части (9). Воспользуемся опять свойством K* условного математического ожидания и свойствами винеровского процесса, имеем учитывая, что
Здесь мы учли тот факт,
Таким образом утверждение следует из равенств (9) – (11) 6) Если 7) Процесс 8) Действительно, из определения стохастического интеграла от простой функции имеем:
Заметим, что для любого j в силу
Отсюда следует утверждение. 2.4. Определим стохастический интеграл для функции из класса Лемма 8. Пусть функция Дата добавления: 2015-01-18 | Просмотры: 804 | Нарушение авторских прав |
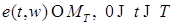 называется простой, если для конечного разбиения
называется простой, если для конечного разбиения 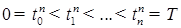 отрезка [0, T ] существуют
отрезка [0, T ] существуют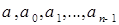 , где
, где 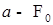 -измерима, а
-измерима, а 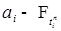 -измерима,
-измерима, 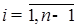 , такие, что
, такие, что 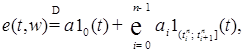 где
где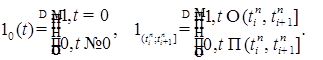
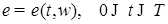 стохастический интеграл
стохастический интеграл 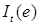 определяем равенством
определяем равенством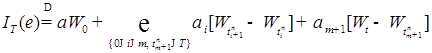
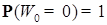 , то
, то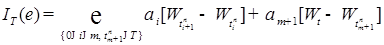 P - п. н.
P - п. н.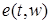 будем использовать также обозначение
будем использовать также обозначение 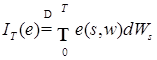 .
.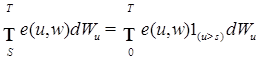 ,
,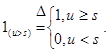
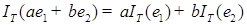 P - п. н..
P - п. н..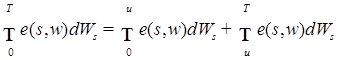 P - п. н. при
P - п. н. при 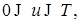
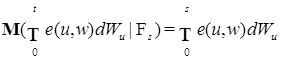 P - п. н.,
P - п. н.,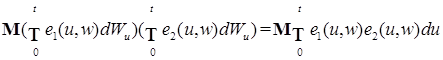 P - п. н., где
P - п. н., где 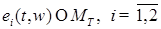 простые функции.
простые функции.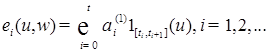 , то имеем
, то имеем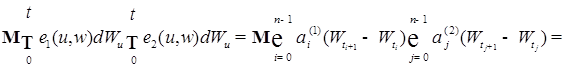
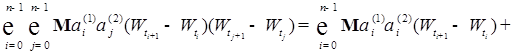
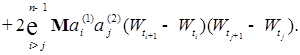 (9)
(9)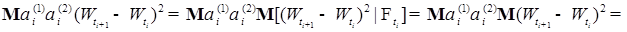
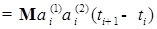 .
.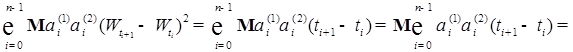
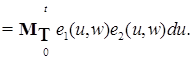 (10)
(10)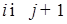
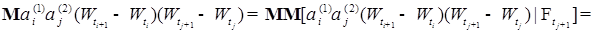
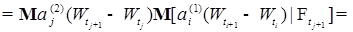
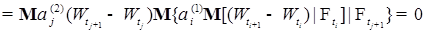
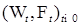 является мартингалом относительно меры Р. Значит
является мартингалом относительно меры Р. Значит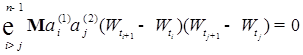 . (11)
. (11)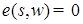 для всех
для всех 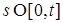 , то P -п.н.
, то P -п.н. 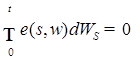 для любого
для любого 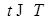 .
.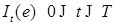 - прогрессивно измерим. Это утверждение следует из теоремы 1 главы 3 и, в частности,
- прогрессивно измерим. Это утверждение следует из теоремы 1 главы 3 и, в частности, 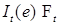 -измерим при каждом
-измерим при каждом 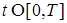 .
.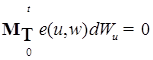 .
.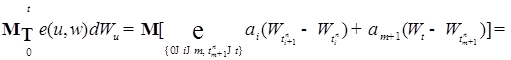
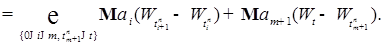
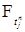 -измеримости
-измеримости 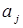 , имеем
, имеем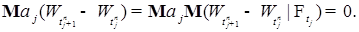
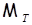 .
.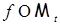 . Тогда найдется последовательность простых функций
. Тогда найдется последовательность простых функций 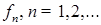 таких, что
таких, что 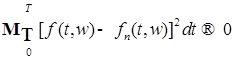 при
при  .
.