Доказательство. Сначала сделаем несколько замечаний
1) Без ограничения общности можно считать функцию 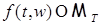 ограниченной, т.е. ограниченной, т.е. 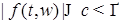 P - п. н. для P - п. н. для 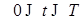 . В противном случае можно перейти от . В противном случае можно перейти от 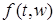 к функциям к функциям 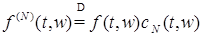 , где , где 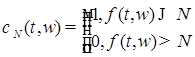
и использовать тот факт, что 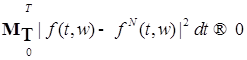 при при 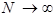 . .
2) Пусть 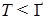 . Если . Если 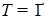 , то сразу можно считать, что функция , то сразу можно считать, что функция 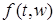 - финитна по t. - финитна по t.
3) Если функция 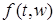 - непрерывна по t P - п. н. почти наверно, то последовательность простых функций строится просто, например, можно положить - непрерывна по t P - п. н. почти наверно, то последовательность простых функций строится просто, например, можно положить 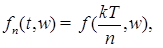 при при 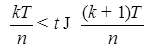 . Тогда доказательство леммы следует из теоремы Лебега о мажорируемой сходимости. . Тогда доказательство леммы следует из теоремы Лебега о мажорируемой сходимости.
4) Если функция 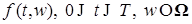 - прогрессивно измерима, то последовательность аппроксимирующих функций можно построить следующим образом. Пусть - прогрессивно измерима, то последовательность аппроксимирующих функций можно построить следующим образом. Пусть 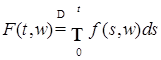 - интеграл Лебега. В силу прогрессивной измеримости - интеграл Лебега. В силу прогрессивной измеримости 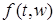 процесс процесс 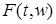 , измерим и при каждом t случайные величины , измерим и при каждом t случайные величины 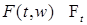 - измеримы. Положим - измеримы. Положим 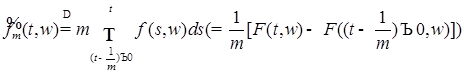 . .
Случайный процесс 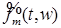 , , 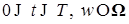 измерим, является неупреждающим и имеет P - п. н. непрерывные траектории. Поэтому, согласно пункту 3), сделанных выше замечаний, существует последовательность неупреждающих ступенчатых функций измерим, является неупреждающим и имеет P - п. н. непрерывные траектории. Поэтому, согласно пункту 3), сделанных выше замечаний, существует последовательность неупреждающих ступенчатых функций 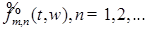 , такая, что , такая, что 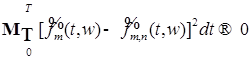 при при  . Заметим, что P - п. н. для почти всех . Заметим, что P - п. н. для почти всех 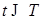 существует производная существует производная 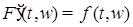 , причем в тех точках, где , причем в тех точках, где 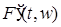 существует P - п. н. существует P - п. н. 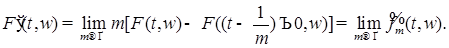 Поэтому для почти всех Поэтому для почти всех 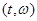 (по мере (по мере 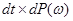 ) ) 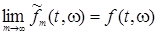 по теореме Лебега о мажорируемой сходимости, имеем по теореме Лебега о мажорируемой сходимости, имеем 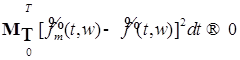
при 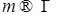 . .
5) Докажем теперь лемму в общем случае. Доопределим функцию 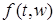 для отрицательных для отрицательных 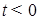 , полагая , полагая 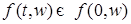 при при 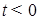 . Пусть . Пусть 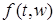 -ограничена и финитна. Положим -ограничена и финитна. Положим 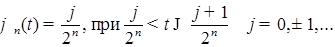 . Заметим, что функция . Заметим, что функция 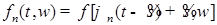 является при каждом фиксированном является при каждом фиксированном 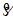 простой. Лемма будет доказана, если показать, что можно выбрать точку простой. Лемма будет доказана, если показать, что можно выбрать точку 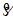 таким образом, что будет выполнено таким образом, что будет выполнено 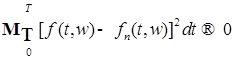 при при  . .
Для этого воспользуемся следующим замечанием: если 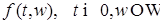 , -измеримая, ограниченная функция, то , -измеримая, ограниченная функция, то 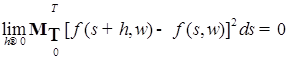 . Действительно, согласно пункту 4), для всякого . Действительно, согласно пункту 4), для всякого 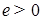 найдется почти всюду такая непрерывная функция найдется почти всюду такая непрерывная функция 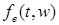 , что , что
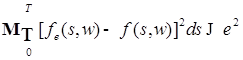 (12). (12).
Тогда в силу неравенства Минковского, имеем
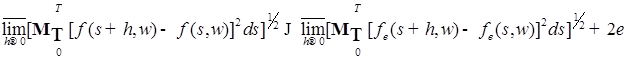 . .
Отсюда в силу произвольности 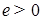 , следует (12). Из (12) вытекает также, что для , следует (12). Из (12) вытекает также, что для 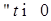
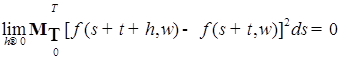
и, в частности,
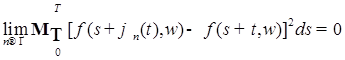 , , 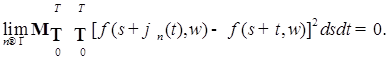
Из последнего равенства следует, что существует такая подпоследовательность чисел 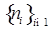 , что для почти всех , что для почти всех 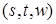 (по мере (по мере 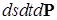 ) )
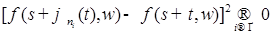
Отсюда, переходя к новым переменным 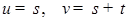 , получим, что для почти всех , получим, что для почти всех 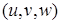 (по мере (по мере 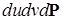 ) ) 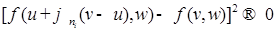 при при 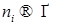 и, значит, найдется такая точка и, значит, найдется такая точка 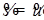 , что , что
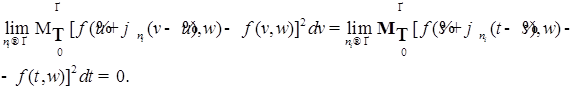
Доказательство закончено.
2.3.1. Замечание. Доказательство леммы 8, приведенное выше, имеет ту ценность, что указывает способ построения простых функций 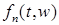 непосредственно по непосредственно по 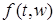 . .
2.4. Итак, пусть 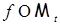 . Тогда, в силу леммы 8, существует последовательность такая, что . Тогда, в силу леммы 8, существует последовательность такая, что 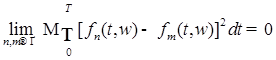 . Следовательно, . Следовательно,
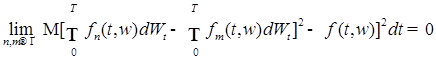 . .
Таким образом, последовательность 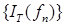 фундаментальна в смысле сходимости в среднеквадратическом, т. е. фундаментальна в смысле сходимости в среднеквадратическом, т. е. 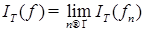 . Значение этого предела, как нетрудно увидеть, не зависит от выбора аппроксимирующей последовательности. Следовательно, определение стохастического интеграла корректно. . Значение этого предела, как нетрудно увидеть, не зависит от выбора аппроксимирующей последовательности. Следовательно, определение стохастического интеграла корректно.
2.5. Свойства стохастических интегралов. Пусть 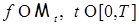 . .
1) 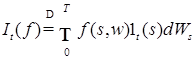 , где , где 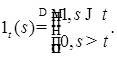
2) 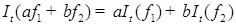 Р -п. н., где Р -п. н., где 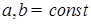 , , 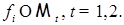
3) 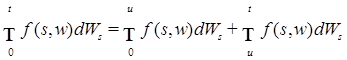 Р -п. н. при Р -п. н. при 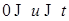 . .
4) 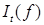 -непрерывная функция t Р -п. н.. -непрерывная функция t Р -п. н..
5) 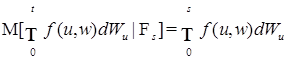 Р -п. н. при Р -п. н. при  . .
6) 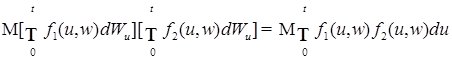 . .
7) Если 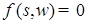 для всех для всех 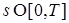 и и 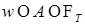 , то , то 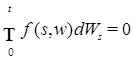 Р -п. н. для Р -п. н. для 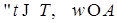 ; ;
8) Процесс 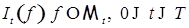 - прогрессивно измерим и, в частности, - прогрессивно измерим и, в частности, 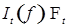 - измерим при каждом - измерим при каждом 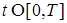 . .
9) Процесс 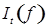 - квадратично интегрируемый мартингал с непрерывными траекториями. - квадратично интегрируемый мартингал с непрерывными траекториями.
2.6. Для построения стохастических интегралов для неупреждающих функций из класса 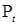 нам понадобятся 2 вспомогательные леммы. нам понадобятся 2 вспомогательные леммы.
2.6.1. Лемма 9. 1) Пусть 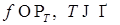 .Тогда найдётся последовательность простых функций .Тогда найдётся последовательность простых функций 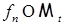 такая, что по вероятности такая, что по вероятности
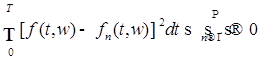 . (13). . (13).
2) Cуществует последовательность простых функций 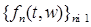 , где , где 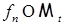 для для 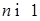 , для которых (13) выполнено как в смысле сходимости по вероятности, так и с вероятностью единица. , для которых (13) выполнено как в смысле сходимости по вероятности, так и с вероятностью единица.
Доказательство этой леммы основано на использовании леммы 8, неравенства Чебышёва и леммы Бореля-Кантелли. Из-за громоздкости доказательства его не приводим.
2.6.2. Лемма 10. Пусть 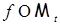 Œ Œ 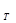 и событие и событие 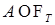 . Тогда . Тогда 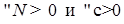
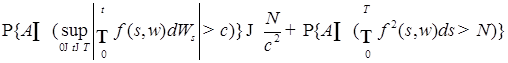 , ,
в частности
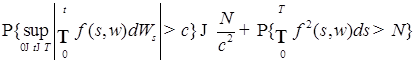 . .
Доказательство. Пусть 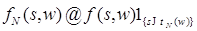 , где , где
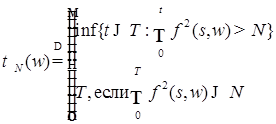 , , 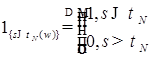 . .
Используя свойство 6) стохастических интегралов, имеем
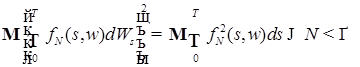 . .
В соответствии со свойствами стохастических интегралов справедливо включение
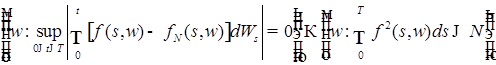 . .
Поэтому для " A Î FT, имеем
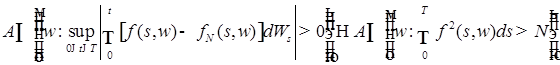 . .
Воспользуемся неравенством Колмогорова (теорема 8 главы 3)
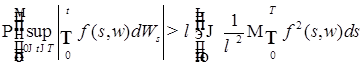 , ,
в силу которого имеем
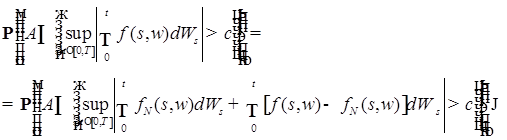 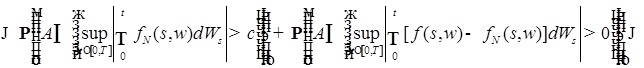
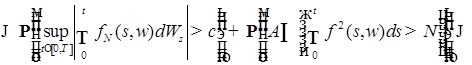
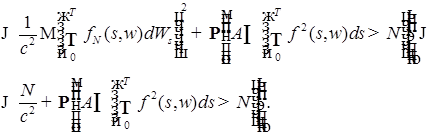
Доказательство закончено.
2.6.3. Замечание. Утверждения лемм 8, 9, 10 остаются справедливыми, если в их формулировках момент Т заменить на марковский момент s, потребовав при этом, чтобы в них 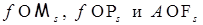 , соответственно. , соответственно.
2.7. С помощью лемм 9 и 10 легко сконструировать стохастический интеграл для неупреждающей функции из класса 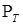 . .
Пусть 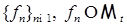 , аппроксимирующие функцию , аппроксимирующие функцию 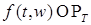 в смысле леммы 9. Тогда очевидно, что для любого в смысле леммы 9. Тогда очевидно, что для любого 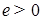
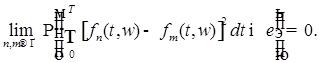
Согласно лемме 10 для любых 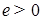 и и 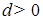
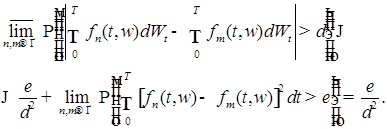
Поэтому в силу произвольности 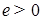 получаем получаем
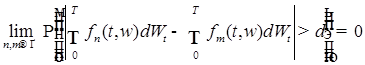 . .
Таким образом, последовательность случайных величин 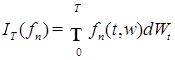 сходится по вероятности к некоторой случайной величине, которую мы обозначим через сходится по вероятности к некоторой случайной величине, которую мы обозначим через 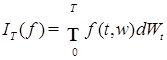 и назовём стохастическим интегралом от функции и назовём стохастическим интегралом от функции 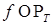 по винеровскому процессу по винеровскому процессу 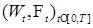 . .
В заключение заметим, легко показать, что значение 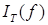 с точностью до множеств нулевой меры Р не зависит от выбора аппроксимирующей последовательности. с точностью до множеств нулевой меры Р не зависит от выбора аппроксимирующей последовательности.
Дата добавления: 2015-01-18 | Просмотры: 684 | Нарушение авторских прав
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|

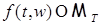 ограниченной, т.е.
ограниченной, т.е. 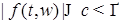 P - п. н. для
P - п. н. для 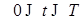 . В противном случае можно перейти от
. В противном случае можно перейти от 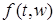 к функциям
к функциям 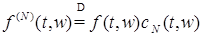 , где
, где 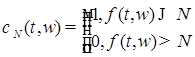
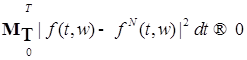 при
при 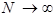 .
.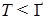 . Если
. Если 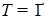 , то сразу можно считать, что функция
, то сразу можно считать, что функция 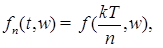 при
при 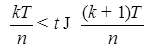 . Тогда доказательство леммы следует из теоремы Лебега о мажорируемой сходимости.
. Тогда доказательство леммы следует из теоремы Лебега о мажорируемой сходимости.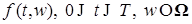 - прогрессивно измерима, то последовательность аппроксимирующих функций можно построить следующим образом. Пусть
- прогрессивно измерима, то последовательность аппроксимирующих функций можно построить следующим образом. Пусть 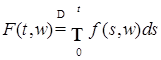 - интеграл Лебега. В силу прогрессивной измеримости
- интеграл Лебега. В силу прогрессивной измеримости 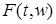 , измерим и при каждом t случайные величины
, измерим и при каждом t случайные величины 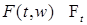 - измеримы. Положим
- измеримы. Положим 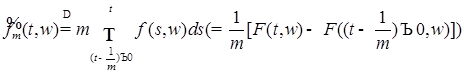 .
.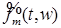 ,
, 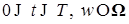 измерим, является неупреждающим и имеет P - п. н. непрерывные траектории. Поэтому, согласно пункту 3), сделанных выше замечаний, существует последовательность неупреждающих ступенчатых функций
измерим, является неупреждающим и имеет P - п. н. непрерывные траектории. Поэтому, согласно пункту 3), сделанных выше замечаний, существует последовательность неупреждающих ступенчатых функций 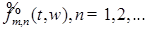 , такая, что
, такая, что 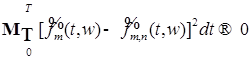 при
при  . Заметим, что P - п. н. для почти всех
. Заметим, что P - п. н. для почти всех 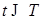 существует производная
существует производная 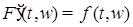 , причем в тех точках, где
, причем в тех точках, где 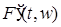 существует P - п. н.
существует P - п. н. 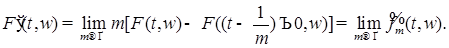 Поэтому для почти всех
Поэтому для почти всех 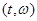 (по мере
(по мере 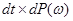 )
) 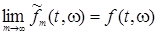 по теореме Лебега о мажорируемой сходимости, имеем
по теореме Лебега о мажорируемой сходимости, имеем 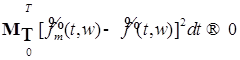
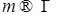 .
.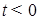 , полагая
, полагая 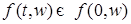 при
при 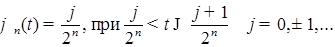 . Заметим, что функция
. Заметим, что функция 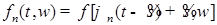 является при каждом фиксированном
является при каждом фиксированном 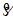 простой. Лемма будет доказана, если показать, что можно выбрать точку
простой. Лемма будет доказана, если показать, что можно выбрать точку 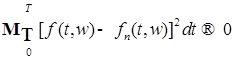 при
при 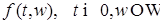 , -измеримая, ограниченная функция, то
, -измеримая, ограниченная функция, то 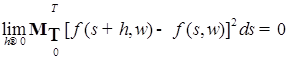 . Действительно, согласно пункту 4), для всякого
. Действительно, согласно пункту 4), для всякого 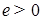 найдется почти всюду такая непрерывная функция
найдется почти всюду такая непрерывная функция 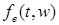 , что
, что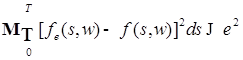 (12).
(12).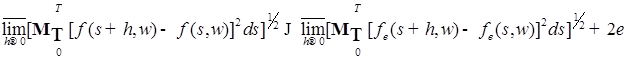 .
.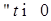
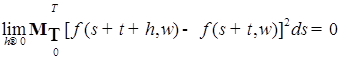
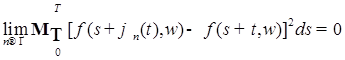 ,
, 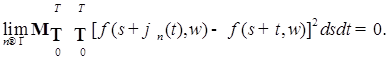
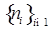 , что для почти всех
, что для почти всех 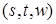 (по мере
(по мере 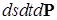 )
)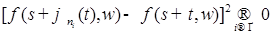
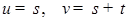 , получим, что для почти всех
, получим, что для почти всех 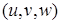 (по мере
(по мере 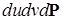 )
) 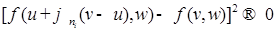 при
при 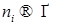 и, значит, найдется такая точка
и, значит, найдется такая точка 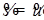 , что
, что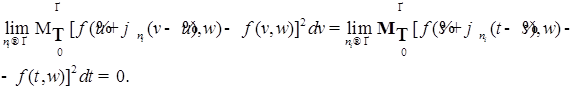
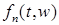 непосредственно по
непосредственно по 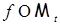 . Тогда, в силу леммы 8, существует последовательность такая, что
. Тогда, в силу леммы 8, существует последовательность такая, что 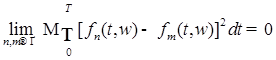 . Следовательно,
. Следовательно,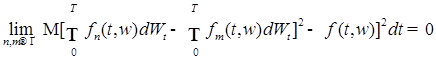 .
.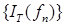 фундаментальна в смысле сходимости в среднеквадратическом, т. е.
фундаментальна в смысле сходимости в среднеквадратическом, т. е. 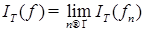 . Значение этого предела, как нетрудно увидеть, не зависит от выбора аппроксимирующей последовательности. Следовательно, определение стохастического интеграла корректно.
. Значение этого предела, как нетрудно увидеть, не зависит от выбора аппроксимирующей последовательности. Следовательно, определение стохастического интеграла корректно.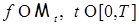 .
.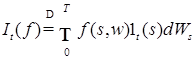 , где
, где 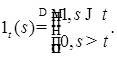
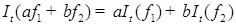 Р -п. н., где
Р -п. н., где 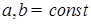 ,
, 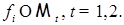
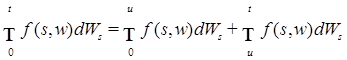 Р -п. н. при
Р -п. н. при 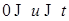 .
.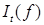 -непрерывная функция t Р -п. н..
-непрерывная функция t Р -п. н..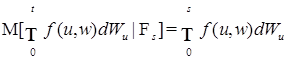 Р -п. н. при
Р -п. н. при  .
.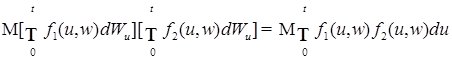 .
.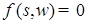 для всех
для всех 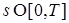 и
и 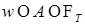 , то
, то 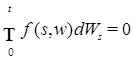 Р -п. н. для
Р -п. н. для 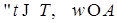 ;
;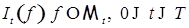 - прогрессивно измерим и, в частности,
- прогрессивно измерим и, в частности, 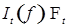 - измерим при каждом
- измерим при каждом 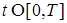 .
.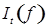 - квадратично интегрируемый мартингал с непрерывными траекториями.
- квадратично интегрируемый мартингал с непрерывными траекториями.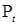 нам понадобятся 2 вспомогательные леммы.
нам понадобятся 2 вспомогательные леммы.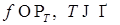 .Тогда найдётся последовательность простых функций
.Тогда найдётся последовательность простых функций 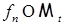 такая, что по вероятности
такая, что по вероятности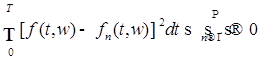 . (13).
. (13).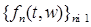 , где
, где 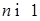 , для которых (13) выполнено как в смысле сходимости по вероятности, так и с вероятностью единица.
, для которых (13) выполнено как в смысле сходимости по вероятности, так и с вероятностью единица.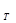 и событие
и событие 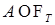 . Тогда
. Тогда 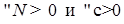
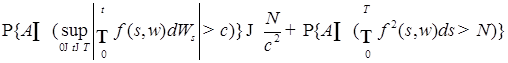 ,
,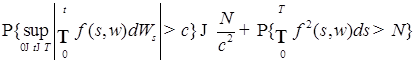 .
.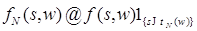 , где
, где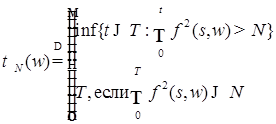 ,
, 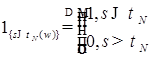 .
.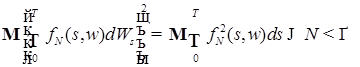 .
.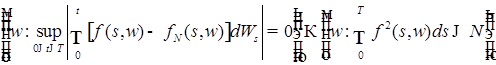 .
.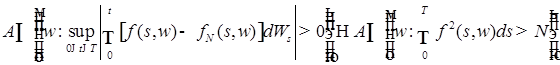 .
.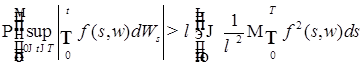 ,
,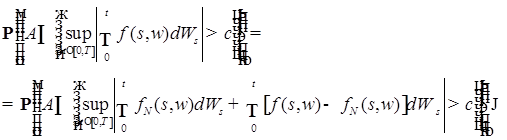
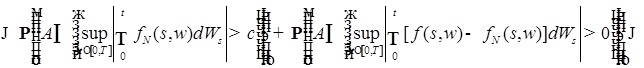
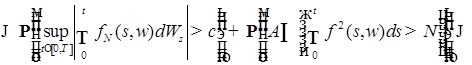
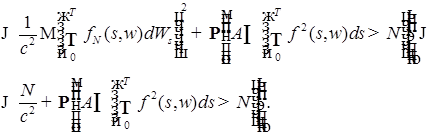
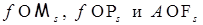 , соответственно.
, соответственно.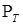 .
.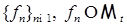 , аппроксимирующие функцию
, аппроксимирующие функцию 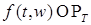 в смысле леммы 9. Тогда очевидно, что для любого
в смысле леммы 9. Тогда очевидно, что для любого 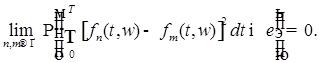
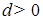
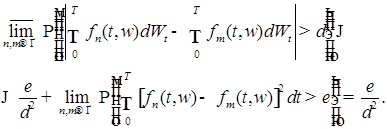
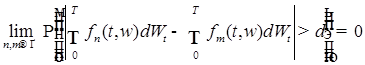 .
.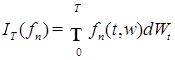 сходится по вероятности к некоторой случайной величине, которую мы обозначим через
сходится по вероятности к некоторой случайной величине, которую мы обозначим через 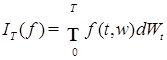 и назовём стохастическим интегралом от функции
и назовём стохастическим интегралом от функции 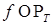 по винеровскому процессу
по винеровскому процессу 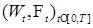 .
.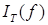 с точностью до множеств нулевой меры Р не зависит от выбора аппроксимирующей последовательности.
с точностью до множеств нулевой меры Р не зависит от выбора аппроксимирующей последовательности.