|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология
|
Доказательство. Отметим, что если выполнены условия i),ii), то выполнены условия теоремы 30 главы 3. Поэтому разрешимость этого уравнения следует из теоремы 30 главы 3
Замечания. 1) Процесс 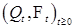 со значениями в со значениями в  , эволюция распределения вероятностей которого описывается уравнением (9), называют обычно процессом гибели-размножения, если , эволюция распределения вероятностей которого описывается уравнением (9), называют обычно процессом гибели-размножения, если  не зависят от не зависят от 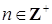 для любого для любого 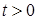 . .
2) Из доказательства теоремы 11 следует, что бесконечная система уравнений (17) является частным случаем системы уравнений Колмогорова, соответствующей марковским процессам с конечным или счетным числом состояний.
3) Систему уравнений (17) можно переписать в другом виде:
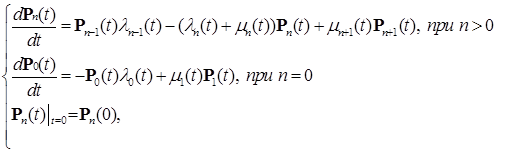 (18) (18)
которая с точки зрения теории дифференциальных уравнений представляет собой бесконечную систему дифференциально-разностных уравнений с граничным условием (18), решение которого допускает вероятностную интерпретацию:  . .
Дата добавления: 2015-01-18 | Просмотры: 708 | Нарушение авторских прав
1 | 2 | 3 | 4 | 5 | 6 |
|
