 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Две предельные теоремы теории очередей
4.1. В данном пункте установим условия существования стационарного решения уравнения (17). Определение. Пусть Для удобства формулировки следующего утверждения приведем условия (R): 1) 2) Обозначим Теорема 16. Пусть выполнены условия (R) и Тогда решение уравнения (17) имеет вид Доказательство. Рассмотрим пространство последовательностей
Относительно этой нормы пространство последовательностей становится банаховым, которое мы обозначим через B. Очевидно, что
Перепишем уравнение (17) в интегральной форме
(27) с учетом (26) можно представить в виде
Отсюда следует, что справедливо неравенство
Поэтому, в силу леммы Гронуолла – Беллмана, из последнего неравенства следует, что 3. Из теоремы 16 вытекает важное утверждение. Теорема 17. Пусть выполнены условия теоремы 16. Тогда выходной поток Доказательство. Достаточно показать, что Отсюда, в силу свойства стохастических интегралов по мартингалу, имеющему ограниченную вариацию (теорема 23 главы 3), и теоремы Фубини, имеем
В силу условий теоремы для
Дата добавления: 2015-01-18 | Просмотры: 691 | Нарушение авторских прав |
 – решение уравнения (17), если для
– решение уравнения (17), если для 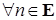 существует
существует  , обозначаемый
, обозначаемый  , то его мы будем называть стационарным решением уравнения (17).
, то его мы будем называть стационарным решением уравнения (17). для
для  ;
; (попутно заметим, отношение
(попутно заметим, отношение  называют коэффициентом нагрузки).
называют коэффициентом нагрузки). .
. .
. для
для  , в нем введем норму:
, в нем введем норму: .
. ,
,  (для любого t). Заметим, что любой
(для любого t). Заметим, что любой  , в силу условий (R), справедливо равенство
, в силу условий (R), справедливо равенство . (26)
. (26) . (27)
. (27)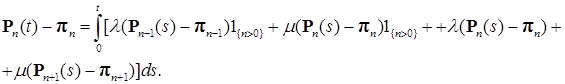
 .
. , т.е.
, т.е.  – решение уравнения (17). Доказательство закончено.
– решение уравнения (17). Доказательство закончено. является пуассоновским с интенсивностью
является пуассоновским с интенсивностью  .
. . Действительно, так как
. Действительно, так как  .
. .
. , поэтому
, поэтому  . Стало быть,
. Стало быть,