 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Простейшие системы массового обслуживания с обратной связью3.1. В данном пункте мы дадим описание простейшей системы массового обслуживания с обратной связью. Пусть на стохастическом базисе
Осуществим прореживание точечного процесса
Как и в §1, введем процессы Очевидно, что
Обозначим
и назовем его процессом (потоком) обратной связи. Через
Положим
для любого момента времени t и
где 3.2. Комментарий. Выше приведенное построение процесса
Рис. 2.
3.3. Для описанных выше систем массового обслуживания справедливы следующие утверждения. Теорема 12. Пусть 1) 2) Теорема 13. Уравнение (23) имеет единственное решение для любого
Доказательство утверждений теорем 12, 13 проводится аналогично доказательству теорем 10, 11 §2, поэтому их не приводим. 3.4. Выведем теперь уравнение, описывающее эволюцию распределения вероятности длины очереди, т.е. Теорема 14. Пусть точечные процессы Пусть Тогда
Доказательство теоремы опирается на утверждение. 3.4.1. Лемма 15. Пусть выполнены условия теоремы 14. Компенсаторы процессов
Доказательство. Достаточно найти компенсатор для потока обратной связи
Отсюда следует утверждение леммы. 3.4.2. Доказательство теоремы 14 почти дословно повторяет доказательство теоремы 10, поэтому его не приводим. 3.5. Возникает вопрос о том, можно ли предложить некоторую методику, позволяющую строить решение уравнения (17) ((24)). Такая методика существует для случая, когда коэффициенты уравнения (17) не зависят от n и t, т.е.
где
Произведем теперь преобразование Лапласа [ ] уравнения (25). Так как,
где Затем, беря обратное преобразование Лапласа относительно
где В общем случае неясно как строить решение уравнения (17). Поэтому возникает проблема разработки асимптотических методов анализа систем массового обслуживания.
Дата добавления: 2015-01-18 | Просмотры: 709 | Нарушение авторских прав |
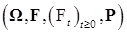 заданы два точечных процесса
заданы два точечных процесса  , с
, с  - измеримыми интенсивностями
- измеримыми интенсивностями  , соответственно, кроме того, на нем задана последовательность бернулли-евских случайных величин
, соответственно, кроме того, на нем задана последовательность бернулли-евских случайных величин  , принимающая значения {0,1}, причем
, принимающая значения {0,1}, причем  . Предположим, что
. Предположим, что  - последовательность марковских моментов, которые нагружают точечный процесс
- последовательность марковских моментов, которые нагружают точечный процесс  . Обозначим
. Обозначим  опциональный случайный процесс с кусочно-постоянными траекториями:
опциональный случайный процесс с кусочно-постоянными траекториями:
 с помощью последовательности
с помощью последовательности  :
: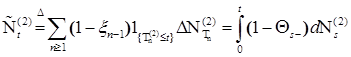

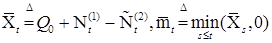 .
. Р – п. н. для любого
Р – п. н. для любого  . Теперь определим простой процесс обслуживания
. Теперь определим простой процесс обслуживания  и назовем его процессом обслуживания для системы с обратной связью. Ясно, что:
и назовем его процессом обслуживания для системы с обратной связью. Ясно, что: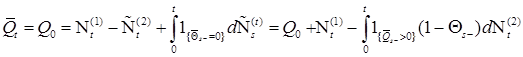
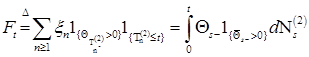
 обозначим процесс:
обозначим процесс: (20)
(20) . Очевидно, что из приведенных построений следует, что
. Очевидно, что из приведенных построений следует, что (21)
(21) , (22)
, (22) - выходной поток.
- выходной поток. имеет простую интерпретацию: на вход системы массового обслуживания (СМО) поступает поток заявок
имеет простую интерпретацию: на вход системы массового обслуживания (СМО) поступает поток заявок  . Затем, поток обслуженных заявок
. Затем, поток обслуженных заявок  прореживается последовательностью
прореживается последовательностью  по следующему правилу: если
по следующему правилу: если  , то она поступает на вход системы массового обслуживания в накопитель необслуженных заявок, т.е. должна быть обслужена снова, последнее означает, что обслуживание произведено некачественно (брак); если
, то она поступает на вход системы массового обслуживания в накопитель необслуженных заявок, т.е. должна быть обслужена снова, последнее означает, что обслуживание произведено некачественно (брак); если  , то заявка обслужена качественно (не брак) и она покидает систему массового обслуживания. Ниже на рис. 2 приведена структурная схема СМО с обратной связью.
, то заявка обслужена качественно (не брак) и она покидает систему массового обслуживания. Ниже на рис. 2 приведена структурная схема СМО с обратной связью.
 Р - п. н. допускает представление:
Р - п. н. допускает представление: ,где
,где  и
и  (23)
(23) .
. .
. и
и  не имеют общих скачков и имеют F – интенсивности
не имеют общих скачков и имеют F – интенсивности  – процесс обслуживания с обратной связью, описываемый (23), причем
– процесс обслуживания с обратной связью, описываемый (23), причем  , не зависящая от
, не зависящая от  , i =1,2. Пусть
, i =1,2. Пусть  .
. удовлетворяет уравнению:
удовлетворяет уравнению: (24)
(24) ,
,  ,
,  ,
,  относительно потока
относительно потока  и меры P имеют для
и меры P имеют для  вид, соответственно:
вид, соответственно: .
. . Пусть
. Пусть  - предсказуемый ограниченный процесс. Очевидно, что определен интеграл Римана-Стилтьеса
- предсказуемый ограниченный процесс. Очевидно, что определен интеграл Римана-Стилтьеса  и существует
и существует  . Так как
. Так как 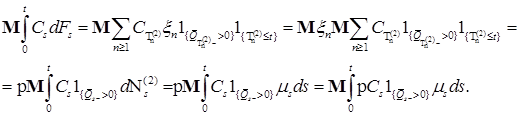
 и основана на использовании производящих функций распределения
и основана на использовании производящих функций распределения  . Напомним, производящая функция для распределения вероятностей
. Напомним, производящая функция для распределения вероятностей  ,
, . Умножим левую и правую части (17) на
. Умножим левую и правую части (17) на 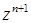 , а затем выполним суммирование по n от нуля до бесконечности. В результате получаем уравнение в частных производных первого порядка с переменными коэффициентами
, а затем выполним суммирование по n от нуля до бесконечности. В результате получаем уравнение в частных производных первого порядка с переменными коэффициентами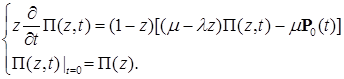 (25)
(25) , то в результате получим из (25)
, то в результате получим из (25)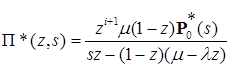 ,
, , и
, и  .
. , легко, с учетом сделанных предположений, получить, что
, легко, с учетом сделанных предположений, получить, что  для любых t, n, i имеет вид:
для любых t, n, i имеет вид:
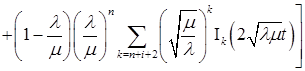 ,
, - обобщенная функция Бесселя первого рода [15]
- обобщенная функция Бесселя первого рода [15]  , Г(l)- гамма функция [15].
, Г(l)- гамма функция [15].