 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Описание простейшей системы массового обслуживания2.1. Пусть на стохастическом базисе Определение. Точечный процесс Определение. Случайную величину Определение. Пусть 2.2. Теорема 7. Пусть
Доказательство. Момент времени б)
Так как
Из (6) следует, что P - п. н.
Очевидно, что
Отсюда следует утверждение теоремы. 2.3. Из теоремы 7 вытекает определение. Определение. Точечный процесс 2.4. Установим условия, при которых уравнение (4) разрешимо. Для этих целей нам понадобится ряд определений. Без ограничения общности можно считать, что Определение. Будем говорить, что (4) имеет сильное решение, если для любого Определение. Пусть Теорема 8. Уравнение (4) имеет единственное решение. Доказательство. Из уравнения (4) следует, что для любого
Отсюда следует, что Заметим, что если решение уравнения (4) существует, то оно имеет кусочно-постоянную траекторию. Поэтому доказательство того факта, что Из последнего равенства следует, что Перейдём теперь к доказательству единственности решения (4). Его мы также проведём по индукции. Пусть
Рассмотрим разность Отсюда следует, что основной шаг индукции доказан, а вместе с ним и утверждение теоремы. 2.5. Комментарии. 1) Из выведенного нами уравнения (4) для простого процесса обслуживания следует описание функционирования системы массового обслуживания (однолинейной). Представим себе, что имеется некоторый поток заявок
Рис. 1.
(
2) Основными задачами теории массового обслуживания являются: а) математическое описание процессов обслуживания 2.6. Выведем теперь уравнения, описывающие эволюцию во времени распределения вероятностей длины очереди. Теорема 9. Пусть для любого
Доказательство. Рассмотрим
Заметим теперь, что:
i) ii) Поэтому (10) с учетом (11) и (12) можно переписать в виде:
Возьмем математическое ожидание относительно левой и правой частей равенства (13). Учитывая, что: i) ii) Имеем
В силу теоремы Фубини и того, что мера Лебега одноточечных множеств равна нулю, последнее равенство можно переписать в виде:
Заметим теперь, что для любого i)
ii)
Поэтому (14) с учетом (15), (16) будет иметь вид (9). Доказательство закончено. 2.7. Следствие 10. Пусть выполнены условия теоремы 9. Тогда для любых
Доказательство. Из доказательства теоремы 9 следует, что для любого 2.8. Приведем теперь условия, выполнение которых обеспечивает разре-шимость бесконечной системы уравнений (17). Теорема 11. Пусть выполняются условия: i) ii) Тогда в классе Дата добавления: 2015-01-18 | Просмотры: 667 | Нарушение авторских прав |
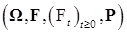 заданы 2 точечных процесса
заданы 2 точечных процесса  , i =1,2, и неотрицательная, интегрируемая,
, i =1,2, и неотрицательная, интегрируемая,  - измеримая случайная величина
- измеримая случайная величина  .
. будем называть входным потоком.
будем называть входным потоком. - измеримую будем называть внутренним состоянием или начальной очередью.
- измеримую будем называть внутренним состоянием или начальной очередью. , а
, а  . Процесс
. Процесс  назовём простым процессом обслуживания или очередью.
назовём простым процессом обслуживания или очередью.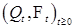 – простой процесс обслуживания. Тогда он допускает представление P –п. н.
– простой процесс обслуживания. Тогда он допускает представление P –п. н. . (4)
. (4) является моментом скачка вниз процесса
является моментом скачка вниз процесса  если и только если выполняются условия: а)
если и только если выполняются условия: а)  ,
, . Поэтому
. Поэтому  - п. н.
- п. н.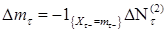 . (5)
. (5) , то из (5) следует, что P - п. н.
, то из (5) следует, что P - п. н. . (6)
. (6) . (7)
. (7) P - п. н. для любого
P - п. н. для любого  , поэтому
, поэтому  P - п. н. для любого
P - п. н. для любого 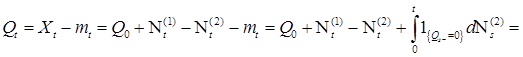

 , определяемый равенством
, определяемый равенством  , называется выходным потоком.
, называется выходным потоком.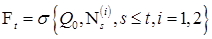 .
.
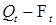 - измеримо, Р - п. н.
- измеримо, Р - п. н.  и обращает (4) в тождество.
и обращает (4) в тождество. – два решения уравнения (4), причём
– два решения уравнения (4), причём  . Будем говорить, что (4) имеет единственное сильное решение, если
. Будем говорить, что (4) имеет единственное сильное решение, если  Р - п. н., где
Р - п. н., где  .
. .
. Р - п. н. для любого
Р - п. н. для любого  .
.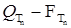 - измеримо. Покажем, что
- измеримо. Покажем, что  - измеримо, где
- измеримо, где  и
и  – марковские моменты, которые нагружают простой процесс обслуживания. Из (4) следует, что при
– марковские моменты, которые нагружают простой процесс обслуживания. Из (4) следует, что при  Р - п. н. Поэтому при
Р - п. н. Поэтому при  Р - п. н.
Р - п. н.  .
. имеет кусочно-постоянные траектории, то Р - п. н. для
имеет кусочно-постоянные траектории, то Р - п. н. для 
 . (8)
. (8) . Пусть
. Пусть  Р - п. н. Покажем, что
Р - п. н. Покажем, что  Р - п. н. Из (8) следует, что Р - п. н.
Р - п. н. Из (8) следует, что Р - п. н.  .
. , поступающий на вход системы, которая представляет собой накопитель заявок и прибор, обслуживающий эти заявки. При этом полагаем, что: а) если прибор обслуживает некоторую заявку, то из накопителя заявки не могут поступить на обслуживающий их прибор; б) если заявка обслужилась прибором, то в прибор поступает следующая заявка и т.д.; в) время, в течение которого заявка обслуживается, определяется как
, поступающий на вход системы, которая представляет собой накопитель заявок и прибор, обслуживающий эти заявки. При этом полагаем, что: а) если прибор обслуживает некоторую заявку, то из накопителя заявки не могут поступить на обслуживающий их прибор; б) если заявка обслужилась прибором, то в прибор поступает следующая заявка и т.д.; в) время, в течение которого заявка обслуживается, определяется как  , где
, где  – последовательность марковских моментов, которая погружает точечный процесс
– последовательность марковских моментов, которая погружает точечный процесс  ,г)после того, как заявка обслужилась, она покидает систему. На рисунке 1 приведена структурная схема системы массового обслуживания
,г)после того, как заявка обслужилась, она покидает систему. На рисунке 1 приведена структурная схема системы массового обслуживания
 - накопитель,
- накопитель,  - начальная очередь).
- начальная очередь).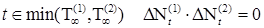 Р - п. н. Пусть
Р - п. н. Пусть  и
и  измеримы интенсивности точечных процессов
измеримы интенсивности точечных процессов  и
и 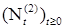 , а
, а  ,
, . Тогда для любого
. Тогда для любого 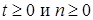
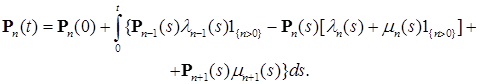 (9)
(9) . В силу условий теоремы, имеем
. В силу условий теоремы, имеем (10)
(10) . (11)
. (11) (12)
(12) (13)
(13) ,
, ,
,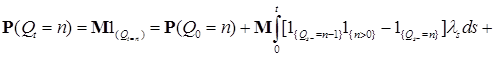
 .
. (14)
(14) имеем:
имеем: (15)
(15)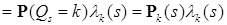 ,
,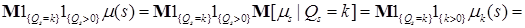
 . (16)
. (16) и почти всех t существует производная
и почти всех t существует производная  и
и  , удовлетворяет уравнению Колмогорова:
, удовлетворяет уравнению Колмогорова: (17)
(17) абсолютно непрерывнa относительно меры Лебега. Отсюда, в силу теоремы Радона – Никодима, существует плотность
абсолютно непрерывнa относительно меры Лебега. Отсюда, в силу теоремы Радона – Никодима, существует плотность  для любого n и t;
для любого n и t; .
. существует единственное решение уравнения (9).
существует единственное решение уравнения (9).