 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Выполнение теоремы об оценкеВ условиях задачи сказано, что недельный рацион должен содержать не менее 4, но не более 6 г кальция; не менее 110 г белка; не более 25 г клетчатки; и этой смеси должно быть ровно 500 г. Предположим, что эти величины могут меняться. Чтобы узнать, на сколько при этом изменится оптимальная стоимость рациона, в соответствии с третьей теоремой двойственности надо воспользоваться теневыми ценами y1-5, которые соответствуют ограничениям прямой задачи. Но для этого вначале следует провести анализ устойчивости теневых цен.
Обозначим изменение минимального содержания кальция Db1; максимального - Db2; минимального содержания белка - Db3; максимального содержания клетчатки - Db4, а массы смеси – Db5 (все эти величины измеряются в граммах). Теперь в таблице 17 вместо свободных членов (b1, b2; b3; b4; b5) следует подставить свободные члены (b1 + Db1, b2 + Db2; b3 + Db3; b4 + Db4; b5 + Db5), т.е. (4 + Db1, 6 + Db2; 44 + Db3; 25 + Db4; 0,5 + Db5). Однако, если мы просто заполним диапазон ячеек электронной таблицы D3:D7 этими выражениями, программа Microsoft Excel не сможет осуществить никаких вычислений над ними, поскольку эти ячейки станут текстовыми. Чтобы избежать этого, вставим перед столбцом Е еще пять столбцов. Теперь столбец свободных членов будет занимать 6 столбцов электронной таблицы (D, E, F, G, H, I). В столбце E запишем коэффициент, который будет умножен на Db1, в столбце F – коэффициент при Db2, и т.д., в столбце I – коэффициент при Db5, а в D – то слагаемое в выражении для свободного члена, которое ни на что не умножается (т.е. прежнее значение свободного члена). Результат представлен в таблице 22.
Теперь новые значения свободных членов, т.е. новый столбец B, записанный в диапазоне D3:I7 электронной таблицы, необходимо подвергнуть тем же линейным преобразованиям, которым подвергались ограничения прямой задачи в таблицах 17-19. Для этого нужно выделить диапазон ячеек D8:D37 и скопировать его на диапазон Е8:I 37. В результате этого новые столбцы симплексных таблиц будут пересчитаны по тем же формулам, что и столбец D. Результаты вычислений приведены в последней строке таблицы 22 и в таблице 23. Заголовки столбцов в таблице 23 отредактированы.
Таблица 22 – Подготовка исходной симплексной таблицы к проведению анализа устойчивости двойственных оценок
Из таблицы 23 видно, что во второй симплексной таблице теперь базисная искусственная переменная у1 = 3,511 + Db1 - 0,011Db3 (см. строку 10 электронной таблицы); а не 3,511, как в таблице 17. Базисная переменная x5 = Оптимальный план прямой задачи примет вид Х* = (0,011 - 0,011Db3 +
Таблица 23 – Анализ устойчивости двойственных оценок
Продолжение таблицы 23
0,011 - 0,011Db3 + Db5 ³ 0 0,489 + 0,011Db3 ³ 0 0,711 - Db1 - 4,211Db3 + 380Db5 ³ 0 1,289 + Db2 + 4,211Db3 - 380Db5 ³ 0 15,222 - 0,022Db3 + Db4 ³ 0
Чтобы решить эту систему, вначале предположим, что меняется только минимальное содержание кальция, т.е. первый свободный член. Тогда Db2 = Db3 = Db4 = Db5 = 0, и система примет вид:
0,489 ³ 0 0,711 - Db1 ³ 0 1,289 ³ 0 15,222 ³ 0 Отсюда Db1 £ 0,711. В первоначальном варианте исходных данных b1 =
Теперь предположим, что меняется только максимальное содержание кальция, т.е. второй свободный член. Тогда Db1 = Db3 = Db4 = Db5 = 0, и система примет вид:
0,489 ³ 0 0,711 ³ 0 1,289 + Db2 ³ 0 15,222 ³ 0 Отсюда Db2 ³ -1,289. Следовательно, двойственная оценка y2 = 0 будет устойчивой при норме максимального содержания кальция от 4,711 г
Следовательно, двойственная оценка y3 = 0,122 будет устойчивой при норме минимального содержания белка от 43,694 г до 44,169 г. Можно сказать, что если потребуется, чтобы в корме содержалось, например, не менее 43,7 г белка, то оптимальная стоимость рациона уменьшится на 0,122*(44 – 43,7) = 0,122*0,3 = 0,0366 (руб.). Если граничное содержание белка составит 44,1 г, то эта стоимость возрастет на 0,122*(44,1 – 44) = 0,0122 (руб.); и т.п. Но если граничное содержание белка составит, например, 43 г, или 10 г, или 44,2 г, или 100 г и т.п., то неизвестно, на сколько изменится оптимум задачи, поскольку при этом исходные данные выйдут за интервал устойчивости двойственных оценок.
При изменении нормы содержания клетчатки Db1 = Db2 = Db3 = Db5 = 0, и система примет вид:
0,489 ³ 0 0,711 ³ 0 1,289 ³ 0 15,222 + Db4 ³ 0 Отсюда Db4 ³ -15,222. Следовательно, двойственная оценка y4 = 0 будет устойчивой при норме содержания клетчатки от 9,778 г до любого значения.
И, наконец, при изменении заданной массы корма Db1 = Db2 = Db3 =
0,489 ³ 0 0,711 + 380Db5 ³ 0 1,289 - 380Db5 ³ 0 15,222 ³ 0 Отсюда -0,003 £ Db5 £ 0,002. Следовательно, двойственная оценка y5 =
Правильность полученных результатов легко проверить, изменяя столбец свободных членов в таблице 22 (ячейки D3:D7). Пока они остаются в пределах найденных интервалов, последняя симплексная таблица (см. таблицу 23) останется допустимой. При этом значения двойственных оценок (коэффициенты в критериальной строке) не изменятся, а оптимум (свободный член в критериальной строке) изменится в соответствии с теоремой об оценке. Например, подставим в ограничение по содержанию белка вместо свободного члена 44 найденное граничное значение 43,694. Для этого просто введем в ячейку D5 это число. При этом результаты вычислений в других ячейках столбца D изменятся. Новые значения в оптимальной симплексной таблице приведены в таблице 24.
Таблица 24 – Проверка результатов анализа устойчивости
Итак, решение задачи изменилось. Новое значение оптимума 7,34. Свободный член изменился на (43,694 - 44 = -0,306), поэтому оптимум должен был измениться на у4*(-0,306) = 0,122*(-0,306)» -0,037. При первоначальном варианте исходных данных оптимум составлял 7,378. Поскольку 7,378 - 0,037 = 7,34, проверка подтвердила правильность всех вычислений.
Кроме того, результаты вычислений в ячейках D37:I37 таблицы 23 как раз показывают, что оптимум задачи равен 7,378 + 0,122Db3 + 4Db5, т.е. непосредственно иллюстрируют теорему об оценке.
Следует обратить внимание, что при подстановке граничных величин свободных членов оптимальный план становится вырожденным (т.е. по крайней мере одна из базисных переменных равна нулю). Например, в таблице 24 x5 = 0. При выходе за пределы найденных интервалов допустимость заключительной таблицы нарушится, т.е. по крайней мере одно из значений в столбце В (ячейках D32:D36) станет отрицательным. Кроме того, следует помнить, что эти интервалы найдены для условий, когда одновременно изменяется только один элемент столбца свободных членов, а остальные остаются неизменными.
Отметим, что если сравнить столбец F3:F37 (коэффициенты при Db2) в таблицах 22-23 со столбцом коэффициентов при х5 I3:I37 (после вставки пяти новых столбцов ячейки I3:I37 стали занимать другой диапазон - N3:N37) в таблицах 17-19, можно убедиться, что они полностью совпадают. Это не удивительно, так как во втором ограничении дополнительная переменная х5 была базисной в исходном опорном плане, и содержимое ячеек F3:F7 в таблице 22 полностью совпадает с содержимым ячеек N3:N7. Следовательно, совпадает и результат их линейного преобразования. То же самое можно сказать про Db4 и х7.
Вопросы и упражнения 1 Определите понятие двойственности. 2 По каким правилам строится двойственная задача? 3 Сформулируйте основную теорему двойственности. 4 Сформулируйте следствие из основной теоремы двойственности. 5 Если ОДП одной из сопряженных задач пуста, какие выводы можно сделать о другой задаче? 6 Как получить решения двойственной задачи из решения исходной задачи симплекс-методом? 7 Сформулируйте теорему о равновесии. 8 Сформулируйте следствие из теоремы о равновесии. 9 Может ли двойственная оценка быть равной нулю, если соответствующее ограничение исходной задачи выполняется, как равенство? 10 В чем заключается экономическая интерпретация теоремы о равновесии? 11 Сформулируйте теорему об оценке. 12 Что такое теневая цена? 13 Что такое сокращенные затраты? 14 В чем заключается понятие устойчивости двойственных оценок? 15 В чем заключается понятие постоптимизационного анализа? 16 Нельзя ли сделать некоторые выводы (и какие) о решении двойственной задачи, если известно, что оптимальный план исходной задачи - вырожденный? 17 Построить и решить задачу, двойственную задаче 11 в разделе 3.4 (пример 3). 18 Построить задачу, двойственную задаче 11 в разделе 3.4 (пример 1), решить ее симплекс-методом и извлечь из заключительной симплексной таблицы решение прямой задачи. 19 Извлечь из решения задачи 11 (раздел 3.4, пример 1) решение двойственной задачи; проверить полученное решение с точки зрения теоремы о равновесии; провести анализ устойчивости двойственных оценок и проверить его результаты. 20 Построить и решить задачу, двойственную задаче 12 в разделе 3.4, решить ее симплекс-методом и извлечь из заключительной симплексной таблицы решение прямой задачи. 21 Извлечь из решения задачи 12 (раздел 3.4) решение двойственной задачи; проверить полученное решение с точки зрения теоремы о равновесии; провести анализ устойчивости двойственных оценок и проверить его результаты. * Не следует путать переменные Y двойственной задачи ни с дополнительными, ни с искусственными переменными, которые в предыдущих разделах иногда обозначались той же буквой. *В любом случае, их значения вычисляют, исходя из коэффициентов критериального ограничения в оптимальной симплексной таблице для прямой задачи, которые находятся в тех столбцах, которые в исходной симплексной таблице были базисными. * Это следует из физического смысла производной (скорость изменения функции в точке). * В разделе 4.2 обозначения y1, y2 и y3 использовались для искусственных переменных при построении расширенной задачи. Поскольку при изучении теории двойственности значения этих переменных использоваться почти не будут, нет необходимости использовать другие буквы латинского алфавита (хотя можно это сделать). Тем не менее, сделаем замечание о том, что не следует путать двойственные переменные с искусственными переменными, которые использовались при решении прямой задачи методом искусственного базиса. * Если при выполнении студентами упражнений для решения двойственной задачи потребуется применить метод искусственного базиса, рекомендуется обозначить искусственные переменные z1, z2 и т.д. * В таблице 19 нет оптимального значения двойственной переменной у5. Это объясняется тем, что она соответствует уравнению прямой задачи, в котором, естественно, нет дополнительной переменной. Однако при решении задачи симплекс-методом в разделе 4.2 в это ограничение вводилась искусственная переменная (ей соответствовал последний столбец N в таблицах 17-19). Отметим, что таблице 19 соответствуют строки 31-37 электронной таблицы. После того, как расширенная задача была решена, все искусственные переменные были исключены из рассмотрения и соответствующие столбцы коэффициентов более не пересчитывались. Если пересчитать их по тем же формулам, что и остальные столбцы (для этого в таблицах 18 и 19 достаточно скопировать формулы в диапазоне К25:К37 на диапазон L25:N37), то в последнем столбце критериальной строки (в N37) коэффициент будет равен 4 (у5 = 4). * Чтобы вычислить по модулю правые части неравенств во второй системе, нет необходимости проводить расчеты вручную. Можно ввести в любую свободную ячейку, например, в ячейку Т32 формулу =D32/G32, которую затем скопировать на диапазон Т33:T36.
Дата добавления: 2015-01-18 | Просмотры: 538 | Нарушение авторских прав |
Полученный ответ будет иметь смысл лишь в том случае, если значения всех переменных будут неотрицательны (т.е. последняя таблица будет допустимой). Поэтому необходимо проверить знак базисных переменных x1, x5, х2, x7, х4; т.е. определить, при каких изменениях свободных членов они будут неотрицательны. Составим систему неравенств:
0,011 ³ 0
0,011 ³ 0
Если предположить, что меняется только минимальное содержание белка, то Db1 = Db2 = Db4 = Db5 = 0, и система примет вид*:
0,011 ³ 0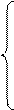
0,011 + Db5 ³ 0