 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Понятие двойственностиДля правильной постановки диагноза необходимо соблюдать алгоритм обследования хирургических больных. Алгоритм обследования хирургических больных особенно важен в экстренных ситуациях. Он включает следующие этапы: 1. Опрос (сбор жалоб и анамнеза). 2. Объективное исследование, прежде всего: - оценка общего состояния; - исследование повреждённой системы (с помощью осмотра, пальпации, перкуссии и аускультации). 3. Специальные методы обследования. Выбирают, в первую очередь, самые простые, но информативные методы. Следует отметить, что после выполнения каждого этапа появляется возможность коррекции следующего. Так, ещё при сборе жалоб и анамнеза врач определяет повреждённую систему, а часто и несколько патологических состояний, наличие которых может обусловливать жалобы. При объективном исследовании он уже целенаправленно проверяет симптомы, характерные для подозреваемых заболеваний, а при назначении специальных методов диагностики, по существу, пытается найти подтверждение своим предположениям или исключить возможность определённых состояний. Соблюдение алгоритма позволяет наиболее полно обследовать больных в кратчайшие сроки. Последовательность проведения методов исследования, указанная выше, желательна, но не обязательна. При обследовании больных, безусловно, необходимо отдавать предпочтение наиболее простым и информативным методам. Важно также отметить, что в ургентной хирургии при обследовании больных многие второстепенные моменты могут быть либо упущены, либо отнесены на более поздние этапы.
Понятие двойственности Рассмотрим задачи линейного программирования в стандартной форме, записанные в матричной форме: max CX
где С = (с1... сn), X = min YB
где Y = (y1... ym). Здесь X, Y - переменные*; A, B, C - константы.
Задача (21) и любая эквивалентная ей задача линейного программирования называется двойственной задаче (20) и любой эквивалентной ей задаче. Подчеркнем, что новых переменных вводится ровно столько, сколько в задаче (20) ограничений, т.е. m. Поскольку любая задача линейного программирования может быть записана в стандартной форме, данное определение позволяет построить двойственную задачу для любой задачи линейного программирования. Исходную задачу, по отношению к которой строится двойственная, иногда еще называют прямой задачей.
Теорема (о сопряженных задачах). Задача, двойственная двойственной, эквивалентна исходной. Доказательство. Построим задачу линейного программирования, двойственную (21). Поскольку определение дает возможность построить двойственную задачу только для задачи в той же форме записи, что и задача (20), вначале преобразуем задачу (21) таким образом, чтобы форма ее записи была такой же. Приведем задачу (21) к стандартной форме на максимум: mах Y(-B)
Транспонируем входящие сюда величины, чтобы порядок действий над векторами и матрицами был таким же, как и в задаче (20): mах -BТYТ
Теперь можно построить двойственную задачу в соответствии со сформулированным определением. Введем строку переменных Z. min Z(-CT)
Эта задача является двойственной к двойственной. Преобразуем ее. mах СZТ
Эта задача эквивалентна задаче (20) с точностью до обозначения. Теорема доказана.
Таким образом, двойственность является взаимной. Пара взаимно двойственных задач называется парой сопряженных задач.
Рассмотрим задачу в канонической форме. Чтобы построить задачу, двойственную к ней, преобразуем ее к стандартной форме.
Построим теперь двойственную задачу. Отметим, что число ограничений задачи возросло в два раза (каждое уравнение преобразовано в два неравенства). Вектор-строку переменных двойственной задачи разобьем на две части, в каждую из которых будет входить равное число переменных, и обозначим его (U,V) = (u1, …, um, v1, …, vm). При этом во всех линейных выражениях компоненты вектора В и матрицы А можно вынести за скобки, а в скобках останется разность векторов U = (u1, …, um) и V = (v1, …, vm). Например, при перемножении строки переменных на первый столбец матрицы А будет получено:
Обозначим U - V = Y. При этом переменные Y = (u1 - v1; …; um – vm) = min YB YA ³ C
Итак, ограничениям-уравнениям поставлены в соответствие неограниченные по знаку переменные. Поскольку двойственность взаимна, можно сказать, что и неограниченным по знаку переменным следует ставить в соответствие ограничения уравнения, а не неравенства. На основании проведенных рассуждений можно сделать вывод, что для построения двойственной задачи не обязательно каждый раз приводить задачу линейного программирования к стандартной форме, а именно нет необходимости преобразовывать уравнения к неравенствам, а не ограниченные по знаку переменные - к неотрицательным. Пусть в задаче в смешанной форме первые m` ограничений – уравнения, а остальные m-m` - неравенства; и первые n` переменных неотрицательны, а остальные n-n` переменных по знаку могут быть любыми. Между задачей линейного программирования в смешанной форме и двойственной ей задачей линейного программирования можно установить следующее соответствие:
Сформулируем ряд правил построения двойственной задачи: а) Переменные двойственной задачи соответствуют ограничениям исходной задачи, а ограничения - переменным. б) Если исходная задача линейного программирования задана на максимум, то двойственная строится на минимум, и наоборот. в) В задаче линейного программирования на максимум в ограничениях-неравенствах должен стоять знак £, а на минимум - ³. г) Ограничениям-неравенствам исходной задачи соответствуют неотрицательные двойственные переменные, а уравнениям – не ограниченные по знаку переменные. д) Неотрицательным переменным исходной задачи соответствуют ограничения неравенства двойственной задачи, а не ограниченным по знаку - уравнения.
Если обе сопряженные задачи записаны в стандартной форме, их называют симметричными сопряженными задачами.
Например, построим задачу, двойственную к следующей задаче: min 2х1 + 3х2 - 4х3 + х5
х1 + 4х2 + х3 + х5 = 15 2х1 - 4х2 - х3 + х4 ³ 3 х1-3, 5 ³ 0 Так как задача на минимум, умножим обе части первого ограничения на -1, чтобы получить знак неравенства ³: -4х1 + 3х2 + х3 - х4 - х5 ³ -10. Так как в прямой задаче три ограничения на пять переменных, двойственная задача будет включать пять ограничений на три переменных. Целевая функция двойственной задачи максимизируется, так как прямая задача поставлена на минимум. Коэффициенты целевой функции двойственной задачи представляют собой свободные члены прямой задачи. Первое ограничение двойственной задачи соответствует переменной х1 прямой задачи, поэтому коэффициенты этого ограничения берут из столбца коэффициентов при х1, а свободный член – из целевой функции прямой задачи. Так как х1 ³ 0, это ограничение – неравенство. Так как двойственная задача на максимум, знак неравенства £. Аналогично строятся второе, третье и пятое ограничения. Четвертое ограничение соответствует переменной х4, знак которой может быть любым. Поэтому оно – уравнение. Переменные y1 и y3 соответствуют первому и третьему ограничениям прямой задачи, которые представляют собой неравенства. Поэтому эти переменные – неотрицательные. Второе ограничение прямой задачи – уравнение, поэтому переменная y2 не ограничена по знаку.
-4y1 + y2 + 2y3 £ 2 3y1 + 4y2 - 4y3 £ 3 y1 + y2 - y3 £ -4 -y1 + y3 = 0 -y1 + y2 £ 1 y1,3 ³ 0 Дата добавления: 2015-01-18 | Просмотры: 930 | Нарушение авторских прав |

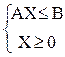 ,
,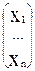 , B =
, B = 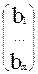 , A =
, A = 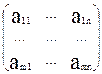

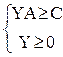 ,
,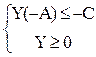
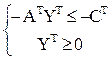
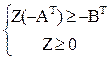
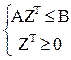
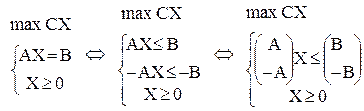
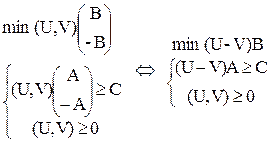
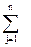 cjxj
cjxj
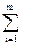 biyi
biyi
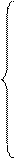
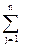 aijxj = bi,
aijxj = bi, 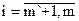
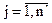
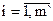
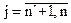
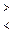 0,
0, 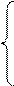 4х1 - 3х2 - х3 + х4 + х5 £10
4х1 - 3х2 - х3 + х4 + х5 £10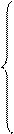 max -10y1 + 15y2 + 3y3
max -10y1 + 15y2 + 3y3