 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Первая теорема двойственностиСопряженные задачи, построенные по рассмотренным выше правилам, обладают рядом свойств, наиболее важные из которых сформулированы в виде трех теорем двойственности. Здесь они будут рассмотрены без доказательства.
Теорема 1 (основная). 1). Сопряженные задачи разрешимы или неразрешимы одновременно, и если разрешимы, то их оптимумы равны. 2). Если целевая функция одной из задач не ограничена, то область допустимых планов другой задачи пуста. Следствие: Для Х0ÎОДП(I), Y0Î ОДП(II) Х0, Y0- оптимальные Û СX0 = Y0B Т.е. допустимые планы сопряженных задач являются оптимальными тогда и только тогда, когда значения целевых функций этих задач на этих планах равны.
Замечания: а) Утверждение, обратное второй части теоремы, не всегда является верным, т.е. если ОДП одной из сопряженных задач пуста, целевая функция другой не обязательно не ограничена. ОДП может быть пуста у обеих задач. б) Логично предположить, что, поскольку сопряженные задачи могут быть разрешимы только одновременно, то, решив исходную задачу симплекс-методом, можно каким-то образом извлечь из этого решения оптимальный план двойственной задачи. Это действительно так.
Оптимальный план двойственной задачи находится в критериальной строке оптимальной симплексной таблицы для прямой задачи. Если ограничение прямой задачи представляет собой неравенство, то при приведении ее к канонической форме в этом ограничении вводится дополнительная переменная. Каждому ограничению соответствует основная переменная двойственной задачи. Ее оптимальное значение находится в том столбце симплексной таблицы для прямой задачи, который соответствует ее дополнительной переменной. Определить значения двойственных переменных, которые соответствуют уравнениям прямой задачи, несколько сложнее, и подробно останавливаться на этом вопросе мы здесь не будем*. Каждой неотрицательной основной переменной прямой задачи соответствует ограничение-неравенство двойственной задачи. При приведении двойственной задачи к канонической форме в каждое такое ограничение также вводится дополнительная переменная. Ее оптимальное значение находится в том столбце симплексной таблицы для прямой задачи, который соответствует ее основной переменной.
В качестве примера рассмотрим оптимальную симплексную таблицу (таблицу 13) для задачи, решенной в разделе 3.3. Задача, двойственная к ней, была построена в разделе 5.2. Если привести ее к канонической форме, она примет вид: max 800у1 + 600у2 + 120у3
0,5у1 + 0,4у2 + 0,1у3 – у5 = 140 у1-5 ³ 0 Три неравенства прямой задачи были преобразованы в уравнения путем введения дополнительных переменных х3, х4 и х5. Этим трем ограничениям соответствуют основные переменные двойственной задачи у1, у2 и у3. Следовательно, их оптимальные значения следует искать в трех последних столбцах таблицы 13: у1* = 125,33; у2* = 0; у3* = 773,33. Двум основным переменным прямой задачи – х1 и х2 – соответствуют два неравенства двойственной задачи. Их преобразовали в уравнения путем введения дополнительных переменных у4 и у5. Следовательно, их оптимальные значения следует искать в двух первых столбцах таблицы 13: у4* = 0; у5* = 0. Таким образом оптимальный план двойственной задачи Y* = (125,33; 0; 773,33; 0; 0). Дата добавления: 2015-01-18 | Просмотры: 911 | Нарушение авторских прав |
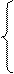 0,8у1 + 0,2у2 + 0,01у3 – у4 = 108
0,8у1 + 0,2у2 + 0,01у3 – у4 = 108