 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Исследование уравнения кривой второго порядка
Линию второго порядка на плоскости в общем виде можно задать с помощью уравнения: Ax 2 + 2 Bxy + Cy 2 + 2 Dx + 2 Ey + F = 0, в котором коэффициенты А, В и С не равны нулю одновременно. Систему координат будем предполагать декартовой прямоугольной. Предположим, что коэффициент В ≠ 0. Для того чтобы упростить общее уравнение, совершим поворот декартовой прямоугольной системы координат на угол φ вокруг начала координат. Старые координаты x и y будут связаны с новыми координатами x ′, y ′ формулами перехода: x = x ′cosφ – y ′sinφ, y = y ′sinφ + y ′cosφ. В новых координатах уравнение примет вид A (x ′cosφ – y ′sinφ)2 + 2 B (x ′cosφ – y ′sinφ)(y ′sinφ + y ′cosφ) + + C (y ′sinφ + y ′cosφ)2 + 2 D (x ′cosφ – y ′sinφ) + 2 E (y ′sinφ + y ′cosφ) + F = 0. Выпишем коэффициент, получающийся после раскрытия скобок и приведения подобных членов при произведении x ′ y ′: B ′ = –2 A cosφ sinφ – 2 B sin2φ + 2 B cos2φ + 2 C sinφ cosφ. Выберем угол φ таким образом, чтобы B ′ был равен нулю: B ′ = (C – A)2cosφ sinφ + 2 B (cos2φ – sin2φ) = 0 или 2 B cos2φ = (A – C)sin2φ. Если А = С, то в качестве угла поворота φ можно положить A ′ x ′2 + C ′ y ′2 + 2 D ′ x ′ + 2 E ′ y ′ + F ′ = 0. Если в это уравнение входит с ненулевым коэффициентом квадрат одной из координат, то при помощи переноса начала координат вдоль соответствующей оси, можно обратить в нуль член с первой степенью этой координаты. В самом деле, пусть, например, A ′ ≠ 0. Перепишем уравнение в виде A ′(x ′2 + Дополним выражение в скобках до полного квадрата, получим A ′ или A ′ Если мы сделаем перенос начала координат, определенный формулами x ′′ = x ′ + y ′′ = y ′, то уравнение примет вид A ′ x ′′2 + C ′ y ′′2 + 2 E ′ y ′′ + F ′′ = 0. Если С ′ ≠ 0, то выделяем полный квадрат со слагаемыми, содержащими y ′′ и, делая перенос начала координат вдоль оси Oy, получим еще более упрощенное уравнение. Рассматривая в упрощенных уравнениях различные комбинации знаков коэффициентов, приходим к следующей теореме. Теорема. Пусть в декартовой системе координат задано уравнение второго порядка Ax 2 + 2 Bxy + Cy 2 + 2 Dx + 2 Ey + F = 0. Тогда существует такая декартова прямоугольная система координат, в которой это уравнение принимает один из девяти канонических видов: 1) 2) 3) a 2 x 2 + c 2 y 2 = 0 – уравнение пары мнимых пересекающихся прямых; 4) 5) a 2 x 2 – c 2 y 2 = 0 – уравнение пары пересекающихся прямых; 6) y 2 = 2 px – уравнение параболы; 7) y 2 – a 2 = 0 – уравнение пары параллельных прямых; 8) y 2 + a 2 = 0 – уравнение пары мнимых параллельных прямых; 9) y 2 = 0 – уравнение пары совпавших прямых. Заметим, что уравнению мнимого эллипса и уравнению пары мнимых параллельных прямых не удовлетворяет ни одна точка на действительной плоскости. Собственно линиями второго порядка являются эллипс, гипербола, парабола. Другие случаи линий второго порядка называются вырожденными. Окружность рассматривается как частный случай эллипса. В следующих параграфах подробнее остановимся на невырожденных случаях кривых второго порядка, которые определим через их геометрические свойства и покажем, что линии с этими свойствами сводятся к перечисленным в теореме уравнениям.
Эллипс Определение. Эллипсом называется множество всех точек плоскости, для которых сумма расстояний от двух данных точек, называемых фокусами, есть величина постоянная, большая расстояния между фокусами. Для вывода уравнения эллипса введем на плоскости прямоугольную систему координаты так, чтобы фокусы эллипса лежали на оси абсцисс, а начало координат делило бы расстояние между фокусами пополам. Выведем уравнение эллипса в выбранной системе координат.
Далее, обозначим через r 1 и r 2 расстояния от точки М до фокусов (r 1 = | F 1 M |, r 2 = | F 2 M |). Числа r 1 и r 2 называют фокальными радиусами точки М. Из определения следует, что точка М (x, y) лежит на данном эллипсе тогда и только тогда, когда r 1 + r 2 = 2 a. (1) Чтобы получить искомое уравнение эллипса, нужно в равенстве (1) заменить переменные r 1 и r 2 их выражениями через координаты x и y. Так как F 1 и F 2 расположены на оси Оx, симметрично относительно начала координат, то они имеют соответственно координаты (– с; 0) и (с; 0); учитывая это и применяя формулу расстояния между двумя точками находим
Подставив эти выражения в равенство (1), получаем
Это и есть искомое уравнение эллипса. Однако, для практического использования оно неудобно, поэтому уравнение эллипса обычно приводят к более простому виду. Для этого перенесем второй радикал в правую часть уравнения (3), а затем возведем обе части равенства в квадрат: (x + c)2 + y 2 = 4 a 2 – или a Снова возведем обе части в квадрат: a 2 x 2 – 2 a 2 cx + a 2 c 2 + a 2 y 2 = a 4 – 2 a 2 cx + c 2 x 2. Отсюда (a 2 – c 2) x 2 + a 2 y 2 = a 2(a 2 – c 2). (5) Рассмотрим теперь новую величину
геометрический смысл которой будет раскрыт далее. Так как по условию а > с, то a 2 – c 2 > 0 и, следовательно, b – положительное число. Из равенства (6) имеем b 2 = a 2 – c 2, поэтому уравнение (5) можно переписать в виде b 2 x 2 + a 2 y 2 = a 2 b 2. Разделив обе части на a 2 b 2, окончательно получим
Так как уравнение (7) получено из уравнения (3), то координаты любой точки эллипса, удовлетворяющие уравнению (3), будут удовлетворять и уравнению (7). Однако, при упрощении уравнения (3) обе его части были дважды возведены в квадрат, и могли появиться «лишние» корни, так что уравнение (7) могло оказаться неравносильным уравнению (3). Убедимся в том, что если координаты точки удовлетворяют уравнению (7), то они удовлетворяют и уравнению (3), т.е. уравнения (3) и (7) равносильны. Для этого, очевидно, достаточно показать, что величины r 1 и r 2 для любой точки, координаты которой удовлетворяют уравнения (7), удовлетворяют соотношению (1). Действительно, пусть координаты x и y некоторой точки удовлетворяют уравнению (7). Тогда, подставляя в выражения (2) для r 1 значение Складывая почленно эти равенства, получаем соотношение (1), что и требовалось установить. Итак, любая точка, координаты которой удовлетворяют уравнению (7), принадлежит эллипсу, и наоборот, т.е. (7) – уравнение эллипса. Уравнение (7) называется каноническим (или простейшим) уравнением эллипса. Таким образом, эллипс – это линия второго порядка. Исследуем теперь форму эллипса по его каноническому уравнению (7). Заметим, что уравнение (7) содержит члены только с четными степенями координат х и у, поэтому эллипс симметричен относительно осей Оx и Оy, а также относительно начала координат. В силу сказанного, будет известна форма всего эллипса, если установить вид той его части, которая лежит в I координатном угле. Для этого разрешим уравнение (7) относительно у и получим
Учитывая, что в I четверти
Из равенства (8) вытекают следующие утверждения: 1) 2) при возрастании х от 0 до а значение у уменьшается; 3) если х = а, то у = 0, т. е. точка А (а; 0) лежит на эллипсе; 4) при х > а получаем мнимые значения у, т. е. точек эллипса, у которых х > а, не существует. Итак, частью эллипса, расположенной в I координатном угле, является дуга ВА. Отразив эту дугу симметрично относительно обеих координатных осей, получаем весь эллипс (рис. 40). Замечание. Если а = b, то уравнение (7) принимает вид x 2 + y 2 = a 2. Это уравнение окружности радиуса а. Таким образом, окружность – это частный случай эллипса. Заметим, что эллипс можно получить из окружности радиуса а, если сжать ее в
Оси симметрии эллипса называются его осями, а центр симметрии (точка пересечения осей) – центром эллипса. Точки, в которых эллипс пересекает оси, называются его вершинами. Так как на основании равенства (6) a Ведем еще одну величину, характеризующую форму эллипса. Определение. Эксцентриситетом эллипса называется отношение с / а, где с – половина расстояния между фокусами, а – большая полуось эллипса. Эксцентриситет обычно обозначают буквой ε: ε = с / а. Так как c < a, то 0
Откуда
Из последнего равенства легко получить геометрическое истолкование эксцентриситета эллипса. При очень малом ε числа а и b почти равны, т.е. эллипс близок к окружности. Если же ε близко к единице, то число b мало по сравнению с числом а и эллипс сильно вытянут вдоль большей оси. Следовательно, эксцентриситет эллипса характеризует меру вытянутости эллипса. Как известно, планеты и некоторые кометы движутся по эллиптическим орбитам. Оказывается, что эксцентриситеты планетных орбит очень малы, а кометных – велики, т. е. близки к единице. Таким образом, планеты движутся почти по окружности, а кометы то приближаются к Солнцу (Солнце находится в одном из фокусов), то удаляются от него. Пример. Составить каноническое уравнение эллипса, проходящего через точки М 1(2; 3) и М 2(1; Решение. Пусть искомое уравнение эллипса есть
Положим
решив которую, найдем m = 1/16, n = 1/12, откуда a 2 = 16, b 2 = 12. Следовательно, искомое уравнение эллипса имеет вид
Дата добавления: 2015-01-18 | Просмотры: 2054 | Нарушение авторских прав |
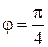 . Если А ≠ С, то получаем
. Если А ≠ С, то получаем 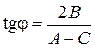 и угол
и угол  . Важно, что такой угол существует, и после поворота системы координат на этот угол рассматриваемое уравнение заменяется на уравнение
. Важно, что такой угол существует, и после поворота системы координат на этот угол рассматриваемое уравнение заменяется на уравнение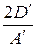 x ′) + C ′ y ′2 + 2 E ′ y ′ + F ′ = 0.
x ′) + C ′ y ′2 + 2 E ′ y ′ + F ′ = 0.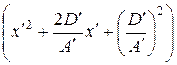 –
– 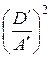 + C ′ y ′2 + 2 E ′ y ′ + F ′ = 0
+ C ′ y ′2 + 2 E ′ y ′ + F ′ = 0 + C ′ y ′2 + 2 E ′ y ′ + F ′ –
+ C ′ y ′2 + 2 E ′ y ′ + F ′ – 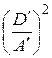 = 0.
= 0.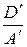 ,
, – уравнение эллипса;
– уравнение эллипса; – уравнение мнимого эллипса;
– уравнение мнимого эллипса;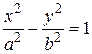 – уравнение гиперболы;
– уравнение гиперболы; Обозначим фокусы эллипса через F 1 и F 2 (рис. 39). Пусть М – произвольная точка эллипса. Расстояние | F 1 F 2| между фокусами обозначим через 2 с, сумму расстояний от точки М до фокусов – через 2 а. Так как по определению эллипса | F 1 M | + | F 2 M | > | F 1 F 2|, то 2 а > 2 с или а > с.
Обозначим фокусы эллипса через F 1 и F 2 (рис. 39). Пусть М – произвольная точка эллипса. Расстояние | F 1 F 2| между фокусами обозначим через 2 с, сумму расстояний от точки М до фокусов – через 2 а. Так как по определению эллипса | F 1 M | + | F 2 M | > | F 1 F 2|, то 2 а > 2 с или а > с. ,
,  . (2)
. (2) +
+ 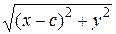 = 2 a. (3)
= 2 a. (3)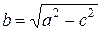 , (6)
, (6)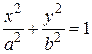 . (7)
. (7) , полученное из (7), после несложных преобразований найдем
, полученное из (7), после несложных преобразований найдем  . Так как | x |< a (это следует из (7)) и
. Так как | x |< a (это следует из (7)) и  < 1, то a +
< 1, то a +  > 0 и поэтому r 1 = a +
> 0 и поэтому r 1 = a +  .
. , рассмотрим уравнение
, рассмотрим уравнение . (8)
. (8) если х = 0, то у = b, т. е. точка В (0; b) лежит на эллипсе;
если х = 0, то у = b, т. е. точка В (0; b) лежит на эллипсе;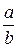 раз вдоль оси Oy. При таком сжатии точка (х; у) перейдет в точку (x; y 1), где
раз вдоль оси Oy. При таком сжатии точка (х; у) перейдет в точку (x; y 1), где 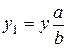 . Подставив
. Подставив  .
. b, то 2 а – длина большой оси симметрии эллипса, 2 b – малой оси. Следовательно, числа а и b являются длинами соответственно большой и малой полуосей эллипса.
b, то 2 а – длина большой оси симметрии эллипса, 2 b – малой оси. Следовательно, числа а и b являются длинами соответственно большой и малой полуосей эллипса.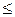 ε < 1, т. е. эксцентриситет эллипса меньше единицы. Учитывая, что c 2 = a 2 – b 2, найдем
ε < 1, т. е. эксцентриситет эллипса меньше единицы. Учитывая, что c 2 = a 2 – b 2, найдем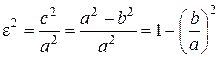 .
. .
. ).
).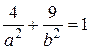 ;
; 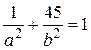 .
. ;
; 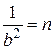 и придем к системе
и придем к системе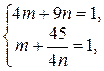
 .
.