 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Асимптоты кривойПонятие асимптоты кривой вводится для кривых, ветви которых уходят в бесконечность. Это может быть в случаях, когда функция не ограничена или когда она задана на неограниченном промежутке. Определение. Прямая линия называется асимптотой кривой Различают три вида асимптот: вертикальные, горизонтальные и наклонные. 1) Вертикальные асимптоты.
О
Таким образом, чтобы найти вертикальные асимптоты, нужно исследовать поведение функции вблизи точек разрыва и границ области определения. Пример 1. Найдем вертикальные асимптоты кривой Решение. Функция 2) Горизонтальные асимптоты.
    у у
М О х Таким образом, горизонтальные асимптоты могут быть только у кривых, заданных на неограниченном промежутке. Для их отыскания нужно найти пределы функции на бесконечности. Пример 2.Найдем горизонтальные асимптоты кривой Решение. Имеем
3)
К N M О
является необходимым и достаточным для того, чтобы прямая
откуда
Из условия (*) следует также, что Таким образом, чтобы найти уравнение наклонной асимптоты, нужно найти коэффициент k по формуле (11.1), подставить его в формулу
и найти коэффициент b. Если пределы в (11.1) и (11.2) существуют и конечны, причем Пример 3. Найдем наклонные асимптоты кривой Решение. Имеем
Дата добавления: 2015-01-18 | Просмотры: 1257 | Нарушение авторских прав |
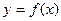 , если расстояние от точки М, лежащей на кривой, до этой прямой стремится к нулю при движении точки М вдоль какой-нибудь части кривой в бесконечность.
, если расстояние от точки М, лежащей на кривой, до этой прямой стремится к нулю при движении точки М вдоль какой-нибудь части кривой в бесконечность.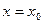 . Расстояние МА от точки
. Расстояние МА от точки 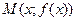 до прямой
до прямой 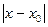 .
. 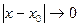 тогда, когда
тогда, когда 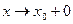 или
или 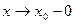 . Чтобы прямая
. Чтобы прямая  стремилась к
стремилась к 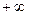 или
или 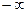 .
.



 А М
А М х
х
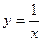 .
.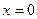 . Исследуем поведение функции при
. Исследуем поведение функции при 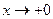 и
и 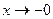 :
: 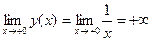 ,
, 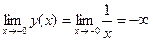 . Отсюда следует, что прямая
. Отсюда следует, что прямая 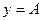 . Расстояние МВ от точки
. Расстояние МВ от точки 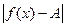 . Чтобы это расстояние стремилось к нулю при
. Чтобы это расстояние стремилось к нулю при 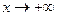 или
или  , нужно, чтобы
, нужно, чтобы 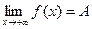 или
или 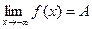 .
.
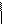 В у = А
В у = А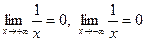 , поэтому прямая
, поэтому прямая  (ось Ох) является горизонтальной асимптотой кривой
(ось Ох) является горизонтальной асимптотой кривой  Так как
Так как 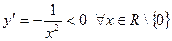 , то функция
, то функция 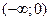 и
и 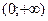 . Поскольку
. Поскольку 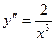 , то
, то 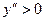 при
при 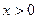 и
и 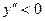 при
при 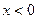 , откуда следует, что
, откуда следует, что  у
у
 О х
О х



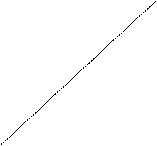


 Наклонные асимптоты.
Наклонные асимптоты.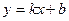 , где
, где 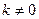 . Чтобы найти постоянные k и b, вычислим расстояние от точки
. Чтобы найти постоянные k и b, вычислим расстояние от точки 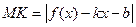 ,
, 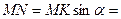
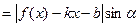 , где
, где 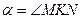 . Угол
. Угол 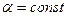 , поэтому
, поэтому 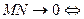
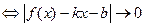 при
при 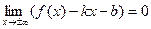 (*)
(*)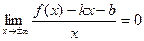 или
или 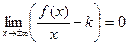 ,
,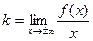 . (11.1)
. (11.1)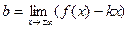 .
.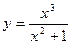 .
.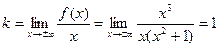 , то есть
, то есть 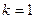 и при
и при 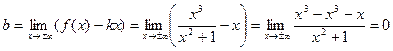 . Таким образом,
. Таким образом, 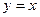 – наклонная асимптота данной кривой и при
– наклонная асимптота данной кривой и при