Степенная функция
Определение 1. Степенной функцией называется функция вида 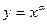 , где , где 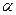 – любое действительное число. – любое действительное число.
Свойства степенной функции зависят от 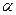 . Рассмотрим случай, когда . Рассмотрим случай, когда 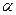 – иррациональное число. – иррациональное число.
Область определения 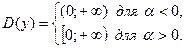 Если Если 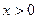 , то , то 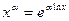 и и 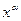 непрерывна как сложная функция в силу непрерывности показательной и логарифмической функций. непрерывна как сложная функция в силу непрерывности показательной и логарифмической функций.
При 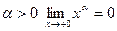 , поэтому функция непрерывна в точке , поэтому функция непрерывна в точке 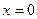 справа. Следовательно, при справа. Следовательно, при 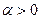 вертикальных асимптот нет. вертикальных асимптот нет.
Если 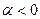 , то , то 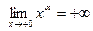 , то есть , то есть 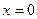 – вертикальная асимптота. – вертикальная асимптота.
Функция не является ни четной, ни нечетной, непериодическая.
Если 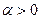 , то , то 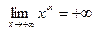 , то есть горизонтальных асимптот нет. , то есть горизонтальных асимптот нет.
Если 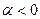 , то , то 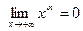  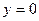 – горизонтальная асимптота. Нетрудно показать, что наклонных асимптот нет. – горизонтальная асимптота. Нетрудно показать, что наклонных асимптот нет.
При 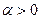 (0; 0) – точка пересечения с осями координат, при (0; 0) – точка пересечения с осями координат, при 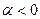 таких точек нет. таких точек нет.
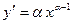  критических точек нет. критических точек нет.
+ 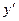 – – 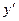
  · ◦ · ◦
0 0
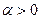 , всюду возрастает в , всюду возрастает в 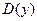 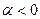 , всюду убывает в , всюду убывает в 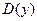
 точек перегиба нет. точек перегиба нет.
+ 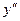 – – 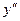 + + 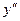
   · · ◦ · · ◦
0 0 0
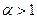 , выпукла вниз , выпукла вниз 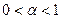 , выпукла вверх , выпукла вверх 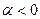 , выпукла вниз , выпукла вниз
у
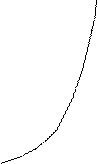 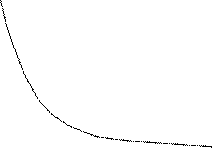   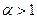

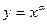 , ,
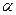 – иррациональное – иррациональное
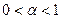
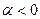
О 1 х
Дата добавления: 2015-01-18 | Просмотры: 617 | Нарушение авторских прав
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|
