 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Наибольшее и наименьшее значения функции на отрезке
Определение 1. Точка Заметим, что точкой экстремума функции может быть только внутренняя точка промежутка, в котором функция определена, поскольку указанные в определении неравенства должны выполняться в некоторой окрестности точки
Теорема 1 (необходимое условие экстремума). Для того чтобы дифференцируемая функция Доказательство. Пусть Определение 2. Точки, в которых производная равна нулю, называются стационарными точками функции. Из доказанной теоремы следует, что точками экстремума функции могут быть только стационарные точки и точки, в которых производная не существует. Такие точки называют подозрительными на экстремум или критическими точками функции. Заметим, что не всякая критическая точка является точкой экстремума. Например, для функции Таким образом, нам надо найти условия, при которых критическая точка является точкой экстремума – достаточные условия экстремума. Есть два типа таких условий. Одни используют производную 1-го порядка, другие – производную 2-го порядка. Рассмотрим достаточное условие экстремума, опирающиеся на 1-ю производную функции. Предположим, что функция 1) 2) 3) При переходе через точку Таким образом, достаточное условие экстремума состоит в следующем: если производная функции при переходе через критическую точку Сформулируем правило исследования функции на экстремум. Нужно: 1) найти область определения функции; 2) найти производную; 3) найти критические точки функции из области определения, то есть точки, в которых производная равна нулю или не существует; 4) определить знак производной слева и справа от каждой из критических точек; 5) на основании достаточного условия экстремума сделать выводы относительно каждой из критических точек. Пример 1. Найдем экстремумы функции Решение. Область определения
0 т.е. при переходе через критическую точку Достаточное условие экстремума функции, опирающееся на 2-ю производную, формулируется следующим образом. Теорема 2. Пусть Доказательство. Пусть Если Замечание. Доказанная теорема позволяет исследовать функции на экстремум только в стационарных точках, т.е. в точках, в которых первая производная равна нулю. Вопрос остается открытым и в том случае, когда вторая производная равна нулю. В этом случае нужно либо изучать поведение высших производных, либо пользоваться правилом, опирающимся на первую производную. Пример 2. Найдем экстремумы функции Решение. Область определения функции Остановимся теперь на задаче о нахождении наибольшего и наименьшего значений функции на отрезке. Пусть функция Таким образом, правило нахождения наибольшего и наименьшего значений функции на отрезке состоит в следующем. Нужно: 1) найти производную данной функции; 2) найти критические точки, принадлежащие данному отрезку; 3) вычислить значения функции в найденных точках и на концах отрезка; 4) из всех найденных значений функции выбрать наибольшее и наименьшее. Пример 3. Найдем наибольшее и наименьшее значения функции Решение. Имеем
Дата добавления: 2015-01-18 | Просмотры: 816 | Нарушение авторских прав |
 называется точкоймаксимума (минимума) функции
называется точкоймаксимума (минимума) функции 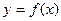 , если существует окрестность
, если существует окрестность 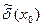 , такая, что
, такая, что 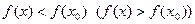 для всех
для всех 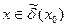 . Точки максимума и минимума функции называются ее точками экстремума, а значения функции в этих точках – экстремумами функции.
. Точки максимума и минимума функции называются ее точками экстремума, а значения функции в этих точках – экстремумами функции.
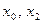 – точки максимума,
– точки максимума, 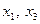 – точки минимума функции
– точки минимума функции  .
.



 О
О 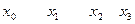 х
х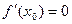 .
.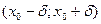 точки
точки 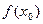 будет наибольшим или наименьшим значением функции
будет наибольшим или наименьшим значением функции 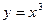 критической является стационарная точка
критической является стационарная точка 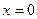 , так как
, так как 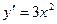 существует для всех х,
существует для всех х, 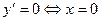 . Но точка
. Но точка 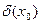 критической точки
критической точки 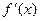 , сохраняющая определенный знак как слева, так и справа от точки
, сохраняющая определенный знак как слева, так и справа от точки 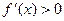 при
при  и
и 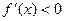 при
при 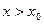 , то есть
, то есть 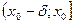 и убывает в промежутке
и убывает в промежутке 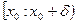 , поэтому значение
, поэтому значение 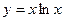 .
.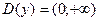 ,
, 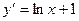 существует во всех точках области определения,
существует во всех точках области определения, 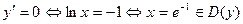 ,
, 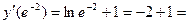
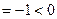 ,
, 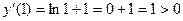 , – +
, – + 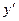


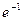
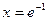 производная меняет знак с минуса на плюс, поэтому
производная меняет знак с минуса на плюс, поэтому 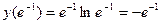 – минимум функции.
– минимум функции. , то
, то  , то
, то  есть производная функции
есть производная функции 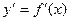 , то по теореме 4 § 8 функция
, то по теореме 4 § 8 функция 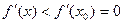 , а справа
, а справа 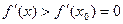 , т.е. при переходе через точку
, т.е. при переходе через точку 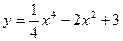 .
.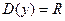 ,
, 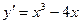 существует всюду в
существует всюду в 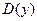 ,
, 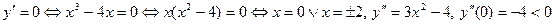

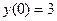 ;
; 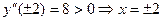 – точки минимума,
– точки минимума, 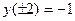 .
.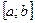 . Тогда по 2-ой теореме Вейерштрасса она принимает на
. Тогда по 2-ой теореме Вейерштрасса она принимает на 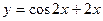 на отрезке
на отрезке 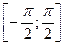 .
.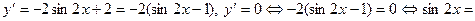
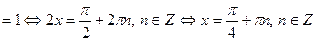 . Из найденных стационарных точек функции только
. Из найденных стационарных точек функции только 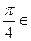
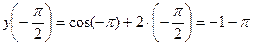 ,
, 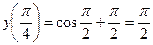 ,
, 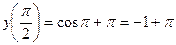 . Видим, что
. Видим, что 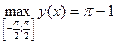 ,
, 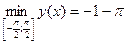 .
.