Показательная функция
Определение 1. Функция вида  называется показательной функцией. называется показательной функцией.
Согласно §13 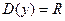 . Поскольку при а = 1 имеем . Поскольку при а = 1 имеем 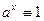 , т.е. функция постоянная, будем предполагать в дальнейшем, что , т.е. функция постоянная, будем предполагать в дальнейшем, что 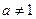 . .
Теорема 1. Если 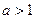 , то функция , то функция 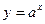 строго возрастает, если строго возрастает, если 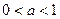 , то , то 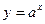 строго убывает. строго убывает.
Доказательство. Пусть  – произвольные действительные числа, – произвольные действительные числа, 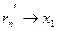 , , 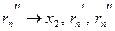 – рациональные числа. Пусть – рациональные числа. Пусть 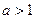 . В силу усиленной плотности множества R найдем рациональные числа . В силу усиленной плотности множества R найдем рациональные числа 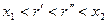 . Начиная с некоторого . Начиная с некоторого  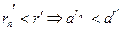 (лемма 2) и (лемма 2) и 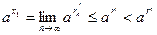 , аналогично , аналогично  , поэтому , поэтому 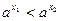 , т.е. , т.е. 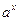 строго возрастает. строго возрастает.
Если 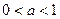 , то , то 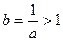 , поэтому , поэтому 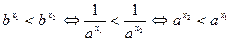 , т.е. , т.е. 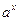 строго убывает. Теорема доказана. строго убывает. Теорема доказана.
Следствие. Показательная функция не имеет точек экстремума.
Теорема 2. Функция 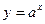 , , 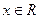 , всюду непрерывна. , всюду непрерывна.
Доказательство. Пусть 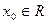 – произвольная точка, – произвольная точка, 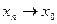 – произвольная – произвольная
последовательность точек. Между числами 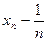 и и 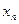 , , 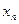 и и  возьмем рациональные числа возьмем рациональные числа 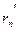 и и 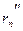 , n = 1, 2, … соответственно (это можно сделать в силу усиленной плотности множества R). Тогда , n = 1, 2, … соответственно (это можно сделать в силу усиленной плотности множества R). Тогда  и и 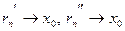 . Поэтому по формуле (13.4) . Поэтому по формуле (13.4) 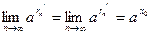 . Поскольку по теореме 1 при . Поскольку по теореме 1 при 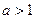 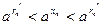 , а при , а при 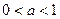 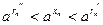 , то по теореме о промежуточной переменной , то по теореме о промежуточной переменной 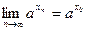 . В силу произвольности последовательности . В силу произвольности последовательности 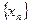 , сходящейся к , сходящейся к  , функция , функция 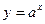 непрерывна в точке непрерывна в точке  по Гейне. Теорема доказана. по Гейне. Теорема доказана.
Следствие. Кривая 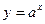 вертикальных асимптот не имеет. вертикальных асимптот не имеет.
Теорема 3. Если 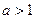 , то , то
1) 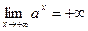 ; 2) ; 2) 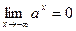 ; 3) ; 3) 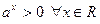 . .
Доказательство. Поскольку 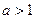 , можно записать , можно записать 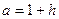 , где , где  . Тогда по неравенству Бернулли . Тогда по неравенству Бернулли 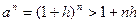 . Какое бы . Какое бы 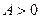 ни взять, найдется ни взять, найдется  такое, что при такое, что при 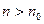 выполняется неравенство выполняется неравенство 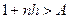 (достаточно взять (достаточно взять 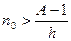 ). Поскольку ). Поскольку 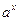 – возрастающая функция, то при – возрастающая функция, то при  имеем имеем 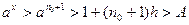 , а это и означает, что , а это и означает, что 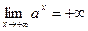 , то есть 1) доказано. , то есть 1) доказано.
Докажем 2). Имеем 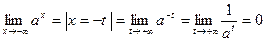 . .
3) следует из 2) и строгого возрастания функции 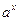 при при 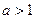 . Теорема доказана. . Теорема доказана.
Следствия. 1) Если 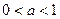 , то , то  , , 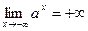 , , 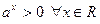 . .
Для доказательства достаточно рассмотреть 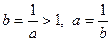 . Тогда . Тогда 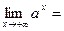  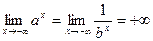 , , 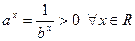 . .
2) Из 2) следует, что 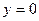 – горизонтальная асимптота при – горизонтальная асимптота при  для для 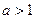 и при и при 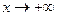 для для 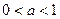 . Наклонных асимптот нет, так как . Наклонных асимптот нет, так как 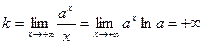 при при 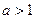 , , 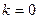 при при  и и 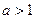 . Аналогичные рассуждения проводятся и для . Аналогичные рассуждения проводятся и для 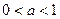 . .
3) область значений показательной функции – множество 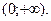 Это следует из теорем 3, 2 и 2-ой теоремы Больцано-Коши. Это следует из теорем 3, 2 и 2-ой теоремы Больцано-Коши.
Поскольку 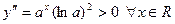 , то кривая выпукла вниз на , то кривая выпукла вниз на 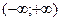 , точек перегиба нет. , точек перегиба нет.
График функции 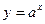 имеет вид: имеет вид:
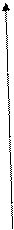  у у 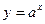 , , 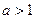
 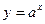 , , 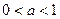
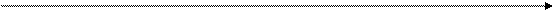
О х
Дата добавления: 2015-01-18 | Просмотры: 569 | Нарушение авторских прав
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|

 называется показательной функцией.
называется показательной функцией.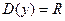 . Поскольку при а = 1 имеем
. Поскольку при а = 1 имеем 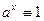 , т.е. функция постоянная, будем предполагать в дальнейшем, что
, т.е. функция постоянная, будем предполагать в дальнейшем, что 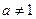 .
.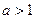 , то функция
, то функция 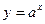 строго возрастает, если
строго возрастает, если 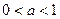 , то
, то  – произвольные действительные числа,
– произвольные действительные числа, 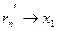 ,
, 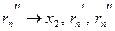 – рациональные числа. Пусть
– рациональные числа. Пусть 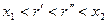 . Начиная с некоторого
. Начиная с некоторого 
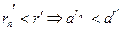 (лемма 2) и
(лемма 2) и 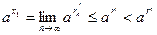 , аналогично
, аналогично  , поэтому
, поэтому 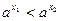 , т.е.
, т.е. 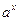 строго возрастает.
строго возрастает.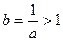 , поэтому
, поэтому 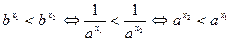 , т.е.
, т.е. 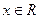 , всюду непрерывна.
, всюду непрерывна.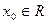 – произвольная точка,
– произвольная точка, 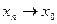 – произвольная
– произвольная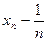 и
и 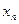 ,
,  возьмем рациональные числа
возьмем рациональные числа 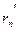 и
и 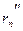 , n = 1, 2, … соответственно (это можно сделать в силу усиленной плотности множества R). Тогда
, n = 1, 2, … соответственно (это можно сделать в силу усиленной плотности множества R). Тогда  и
и 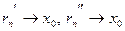 . Поэтому по формуле (13.4)
. Поэтому по формуле (13.4) 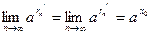 . Поскольку по теореме 1 при
. Поскольку по теореме 1 при 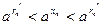 , а при
, а при 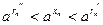 , то по теореме о промежуточной переменной
, то по теореме о промежуточной переменной 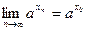 . В силу произвольности последовательности
. В силу произвольности последовательности 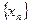 , сходящейся к
, сходящейся к  , функция
, функция 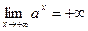 ; 2)
; 2) 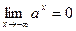 ; 3)
; 3) 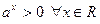 .
.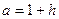 , где
, где  . Тогда по неравенству Бернулли
. Тогда по неравенству Бернулли 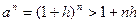 . Какое бы
. Какое бы 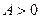 ни взять, найдется
ни взять, найдется 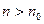 выполняется неравенство
выполняется неравенство 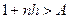 (достаточно взять
(достаточно взять 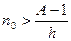 ). Поскольку
). Поскольку  имеем
имеем 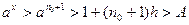 , а это и означает, что
, а это и означает, что 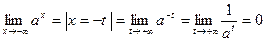 .
. ,
, 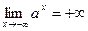 ,
, 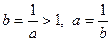 . Тогда
. Тогда 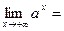

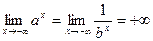 ,
, 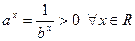 .
.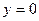 – горизонтальная асимптота при
– горизонтальная асимптота при  для
для 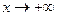 для
для 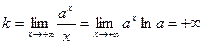 при
при 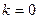 при
при 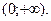 Это следует из теорем 3, 2 и 2-ой теоремы Больцано-Коши.
Это следует из теорем 3, 2 и 2-ой теоремы Больцано-Коши.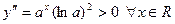 , то кривая выпукла вниз на
, то кривая выпукла вниз на 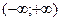 , точек перегиба нет.
, точек перегиба нет.
 у
у