Выпуклые кривые. Точки перегиба кривой
Определение 1. Кривая 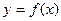 называется выпуклой вверх (выпуклой вниз) в точке называется выпуклой вверх (выпуклой вниз) в точке 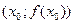 , если в некоторой окрестности точки , если в некоторой окрестности точки  она лежит ниже (соответственно, выше) касательной она лежит ниже (соответственно, выше) касательной  . Если кривая выпукла вверх (вниз) в каждой точке некоторого промежутка, то она называется выпуклой вверх (вниз) на этом промежутке. . Если кривая выпукла вверх (вниз) в каждой точке некоторого промежутка, то она называется выпуклой вверх (вниз) на этом промежутке.
В точке 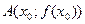 кривая выпукла вверх, в точке кривая выпукла вверх, в точке  выпукла вниз. выпукла вниз.
| |  у у
 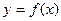
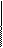  А А
 В В
 О О  х х
Теорема 1 (достаточные условия выпуклости кривой). Пусть функция 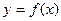 определена, непрерывна и дифференцируема в некоторой окрестности точки определена, непрерывна и дифференцируема в некоторой окрестности точки  и имеет в этой точке 2-ю производную. Тогда, если и имеет в этой точке 2-ю производную. Тогда, если  , то кривая , то кривая 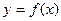 выпукла вниз в точке выпукла вниз в точке 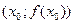 , если , если  , то в этой точке кривая , то в этой точке кривая 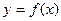 выпукла вверх. выпукла вверх.
Доказательство. Запишем уравнение касательной к кривой  в точке в точке 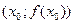 в виде в виде  и рассмотрим функцию и рассмотрим функцию  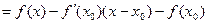 . Имеем . Имеем  . Если . Если  , то и , то и  , и по второму достаточному условию экстремума функция , и по второму достаточному условию экстремума функция  имеет в точке имеет в точке  минимум. Поскольку минимум. Поскольку 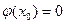 , то в некоторой окрестности точки , то в некоторой окрестности точки  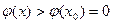 для всех для всех  , то есть , то есть   кривая кривая 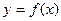 выпукла вниз в точке выпукла вниз в точке 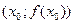 . .
Если  , то и , то и  , и аналогично показывается, что , и аналогично показывается, что  из некоторой окрестности точки из некоторой окрестности точки  , поэтому , поэтому  в этой проколотой окрестности в этой проколотой окрестности  кривая кривая 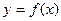 выпукла вверх в точке выпукла вверх в точке 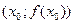 . Теорема доказана. . Теорема доказана.
Определение 2. Точка 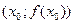 называется точкой перегиба кривой называется точкой перегиба кривой 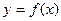 , если в этой точке кривая переходит с одной стороны касательной на другую, то есть если в некоторой окрестности точки , если в этой точке кривая переходит с одной стороны касательной на другую, то есть если в некоторой окрестности точки  для всех для всех  все точки кривой лежат по одну сторону от касательной, а для всех все точки кривой лежат по одну сторону от касательной, а для всех 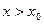 – по другую. – по другую.
 у у
| | | | | | | |
Точка 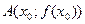 – точка перегиба кривой – точка перегиба кривой 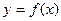 . .
| | | |  | | |
  А А
 О О  х х
Теорема 2 (необходимое условие точки перегиба). Для того, чтобы кривая 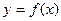 имела перегиб в точке имела перегиб в точке 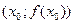 , необходимо, чтобы в точке , необходимо, чтобы в точке  2-я производная функции 2-я производная функции  либо не существовала, либо была равна нулю. либо не существовала, либо была равна нулю.
Доказательство. Предположим противное, то есть что 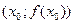 – точка перегиба кривой – точка перегиба кривой 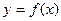 и существует и существует  , причем , причем  . Тогда либо . Тогда либо  и по предыдущей теореме кривая выпукла вниз в точке и по предыдущей теореме кривая выпукла вниз в точке 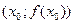 , либо , либо  и кривая выпукла вверх в этой точке. И в том, и в другом случае кривая лежит по одну сторону от касательной в некоторой окрестности точки и кривая выпукла вверх в этой точке. И в том, и в другом случае кривая лежит по одну сторону от касательной в некоторой окрестности точки 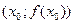 , то есть эта точка не является точкой перегиба. Полученное противоречие доказывает теорему. , то есть эта точка не является точкой перегиба. Полученное противоречие доказывает теорему.
Теорема 3 (достаточное условие точки перегиба). Пусть функция 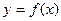 дифференцируема в некоторой окрестности дифференцируема в некоторой окрестности 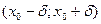 точки точки  , на интервалах , на интервалах 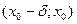 и и  существует 2-я производная существует 2-я производная  , причем она сохраняет знак на каждом из этих интервалов. Тогда, если на , причем она сохраняет знак на каждом из этих интервалов. Тогда, если на 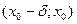 и и  знаки 2-ой производной различны, то точка знаки 2-ой производной различны, то точка 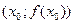 является точкой перегиба кривой является точкой перегиба кривой 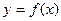 , если одинаковы, то перегиба нет. , если одинаковы, то перегиба нет.
Доказательство. Пусть  – уравнение касательной в точке – уравнение касательной в точке 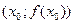 к кривой к кривой  . Рассмотрим функцию . Рассмотрим функцию   . Применим к разности . Применим к разности 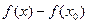 формулу Лагранжа: формулу Лагранжа: 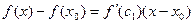 , где , где 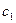 – точка между х и – точка между х и  . Получим . Получим  . Вновь применим формулу Лагранжа, теперь к разности . Вновь применим формулу Лагранжа, теперь к разности 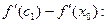 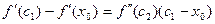 , где , где  – точка между – точка между 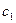 и и  . Таким образом, . Таким образом, 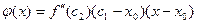 . Заметим, что точки х и . Заметим, что точки х и 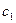
| | | | находятся по одну сторону от точки  , поэтому , поэтому  . Следовательно, знак . Следовательно, знак  зависит от знака зависит от знака  . Если . Если  имеет разные знаки на интервалах имеет разные знаки на интервалах 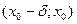 и и  , то , то  имеет имеет
| |
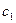 х х
| | •  • • • • • •
•  • • • • • •
разные знаки, когда 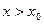 и и  , т.е. , т.е.  меняет знак при переходе через точку меняет знак при переходе через точку  . Это означает, что кривая . Это означает, что кривая 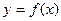 лежит с одной стороны от точки лежит с одной стороны от точки 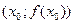 выше, а с другой стороны – ниже касательной, т.е. выше, а с другой стороны – ниже касательной, т.е. 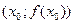 – точка перегиба. – точка перегиба.
Если же на интервалах 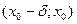 и и   имеет один и тот же знак, то имеет один и тот же знак, то  имеет один знак, имеет один знак,  тоже сохраняет знак на интервале тоже сохраняет знак на интервале 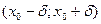 , поэтому точка , поэтому точка 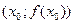 не является точкой перегиба. Теорема доказана. не является точкой перегиба. Теорема доказана.
Сформулируем правило отыскания точек перегиба кривой 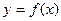 . Нужно: . Нужно:
1) найти область определения 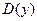 ; ;
2) вычислить  ; ;
3) найти точки из 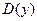 , в которых , в которых  не существует или равна нулю; не существует или равна нулю;
4) исследовать знак  слева и справа от каждой из найденных точек; слева и справа от каждой из найденных точек;
5) сделать вывод об этих точках на основании достаточного условия точки перегиба.
Пример. Найдем точки перегиба и интервалы выпуклости вверх и вниз функции 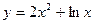 . .
Поэтому точка 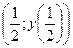 , то есть точка , то есть точка 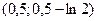 – точка перегиба кривой, – точка перегиба кривой, 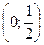 – –
| | Решение. Область определения  не существует в точке не существует в точке 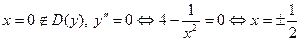 , причем , причем  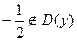 . Отметим точки 0 и . Отметим точки 0 и 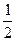 на числовой прямой и определим знак на числовой прямой и определим знак 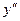 на каждом из двух полученных интервалов области определения: на каждом из двух полученных интервалов области определения:  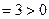 . – + . – + 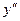
 
Поэтому точка 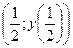 , т.е. точка , т.е. точка 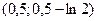 – точка перегиба кривой, – точка перегиба кривой, 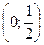 –интервал выпуклости вверх кривой, –интервал выпуклости вверх кривой,  – интервал выпуклости вниз кривой. – интервал выпуклости вниз кривой.
Замечание. Определение выпуклой кривой нами было дано с помощью касательной к кривой, т.е. соответствующая функция предполагалась дифференцируемой. Есть и другие, более общие определения, не предполагающие дифференцируемости функции. Теоремы при этом доказываются несколько более сложно.
Дата добавления: 2015-01-18 | Просмотры: 1157 | Нарушение авторских прав
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|

 у
у
 • • •
• • •
 • • •
• • •
 не существует в точке
не существует в точке 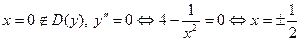 , причем
, причем 
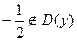 . Отметим точки 0 и
. Отметим точки 0 и 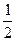 на числовой прямой и определим знак
на числовой прямой и определим знак  на каждом из двух полученных интервалов области определения:
на каждом из двух полученных интервалов области определения: 
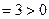 . – +
. – + 


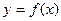 называется выпуклой вверх (выпуклой вниз) в точке
называется выпуклой вверх (выпуклой вниз) в точке 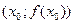 , если в некоторой окрестности точки
, если в некоторой окрестности точки  она лежит ниже (соответственно, выше) касательной
она лежит ниже (соответственно, выше) касательной  . Если кривая выпукла вверх (вниз) в каждой точке некоторого промежутка, то она называется выпуклой вверх (вниз) на этом промежутке.
. Если кривая выпукла вверх (вниз) в каждой точке некоторого промежутка, то она называется выпуклой вверх (вниз) на этом промежутке.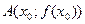 кривая выпукла вверх, в точке
кривая выпукла вверх, в точке  выпукла вниз.
выпукла вниз.


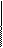
 А
А В
В О
О  х
х , то кривая
, то кривая  , то в этой точке кривая
, то в этой точке кривая  в точке
в точке  и рассмотрим функцию
и рассмотрим функцию 
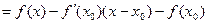 . Имеем
. Имеем  . Если
. Если  , и по второму достаточному условию экстремума функция
, и по второму достаточному условию экстремума функция  имеет в точке
имеет в точке 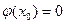 , то в некоторой окрестности точки
, то в некоторой окрестности точки 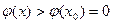 для всех
для всех  , то есть
, то есть 
 кривая
кривая  , и аналогично показывается, что
, и аналогично показывается, что  из некоторой окрестности точки
из некоторой окрестности точки  в этой проколотой окрестности
в этой проколотой окрестности  все точки кривой лежат по одну сторону от касательной, а для всех
все точки кривой лежат по одну сторону от касательной, а для всех 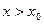 – по другую.
– по другую. у
у

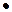 А
А О
О  либо не существовала, либо была равна нулю.
либо не существовала, либо была равна нулю. , причем
, причем  . Тогда либо
. Тогда либо 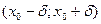 точки
точки 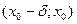 и
и  существует 2-я производная
существует 2-я производная  , причем она сохраняет знак на каждом из этих интервалов. Тогда, если на
, причем она сохраняет знак на каждом из этих интервалов. Тогда, если на 
 . Применим к разности
. Применим к разности 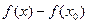 формулу Лагранжа:
формулу Лагранжа: 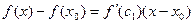 , где
, где 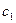 – точка между х и
– точка между х и  . Вновь применим формулу Лагранжа, теперь к разности
. Вновь применим формулу Лагранжа, теперь к разности 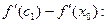
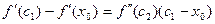 , где
, где  – точка между
– точка между 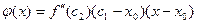 . Заметим, что точки х и
. Заметим, что точки х и  . Следовательно, знак
. Следовательно, знак  . Если
. Если 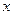
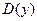 ;
;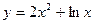 .
.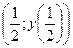 , то есть точка
, то есть точка 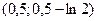 – точка перегиба кривой,
– точка перегиба кривой, 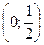 –
–
 – интервал выпуклости вниз кривой.
– интервал выпуклости вниз кривой.