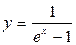|
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Полное исследование функций и построение их графиковЕсть различные схемы полного исследования функций. Одна из возможных схем следующая. Нужно: 1. Установить область определения функции. Исследовать функцию на четность, нечетность, периодичность. Установить точки разрыва и характер разрыва. Исследовать поведение функции на границе области определения. Найти асимптоты. Найти точки пересечения графика функции с осями координат. 2. Исследовать функцию на экстремум. Установить интервалы монотонности функции. 3. Исследовать направление выпуклости графика функции, найти точки перегиба. 4. Построить график функции, используя все полученные результаты. При необходимости вычислить значения функции при некоторых значениях ее аргумента. Пример. Проведем полное исследование функции Решение. Знаменатель дроби равен нулю в точке Исследуем функцию на экстремум и на монотонность:
Исследуем график функции на выпуклость и точки перегиба:
Точек перегиба нет, так как
О х -1
Рассмотрим теперь основные элементарные функции и установим их свойства.
Дата добавления: 2015-01-18 | Просмотры: 726 | Нарушение авторских прав |
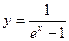 и построим ее график.
и построим ее график.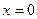 , поэтому
, поэтому 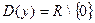 – симметрична относительно начала координат. Функция не является четной и нечетной, так как
– симметрична относительно начала координат. Функция не является четной и нечетной, так как 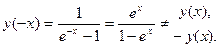 Функция не является периодической, так как не существует только в одной точке
Функция не является периодической, так как не существует только в одной точке 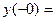
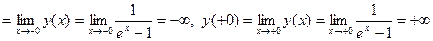 , поэтому
, поэтому 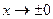 . Горизонтальные асимптоты:
. Горизонтальные асимптоты: 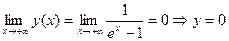 – горизонтальная асимптота при
– горизонтальная асимптота при 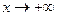 ;
; 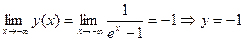 – горизонтальная асимптота при
– горизонтальная асимптота при  . Так как
. Так как 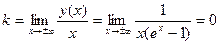 , то наклонных асимптот нет. С осью Оу график не пересекается, так как точка
, то наклонных асимптот нет. С осью Оу график не пересекается, так как точка 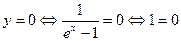 , что невозможно, поэтому с осью Ох пересечения тоже нет.
, что невозможно, поэтому с осью Ох пересечения тоже нет.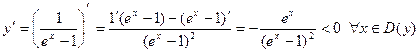 , поэтому точек экстремума нет,
, поэтому точек экстремума нет, 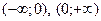 – интервалы убывания функции. _ _
– интервалы убывания функции. _ _ 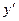

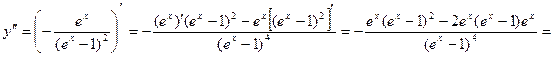
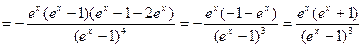 . Видим, что числитель всегда положителен, а знаменатель больше нуля при
. Видим, что числитель всегда положителен, а знаменатель больше нуля при 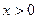 , и меньше нуля при
, и меньше нуля при 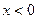 , то есть распределение знаков
, то есть распределение знаков 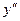 следующее: – +
следующее: – + 
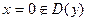 ,
, 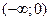 – интервал выпуклости вверх,
– интервал выпуклости вверх, 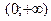 – интервал выпуклости вниз.
– интервал выпуклости вниз.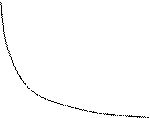

 Строим график функции, используя все полученные результаты.
Строим график функции, используя все полученные результаты. у
у