|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология
|
Условия постоянства, возрастания и убывания функции
| Вид нити
| МЗКРС
(Россия)
| Этикон (США)
| Аутосьюче (США)
| Девис&Гек (США)
| БиБраун Германия
| Кетгут ГмбХ Германия
| Резорба Германия
| | Рассасывающиеся нити
| | Рассасывающаяся плетеная синтетическая нить
| ПГА (Полигликолид) (фиолет.)
| Викрил (фиолет.)
| Полисорб (фиолет., неокраш.)
| Дексон-2, Дексон S (неокраш.) Дексон С (бежевый, зеленый)
| Сафил (зеленый, бежевый)
| Марлин (фиолет.)
| ПГА (фиолет.)
| | Рассасывающаяся монофиламентная нить
| ПДО (фиолет.)
| Монокрил (бесцветн.) ПДС-2 (фиолет.)
| Биосин (фиолет.)
| Максон (зеленый)
| Мавносин (фиолет.)
| –
| Капролон (фиолет.)
| | Нерассасывающиеся нити
| | Полипропиленовая нить
| Полипропилен (синий)
| Пролей (синий)
| Серджипло (синий)
| Сурджилен (синий)
| Премилен (голубой)
| Марилон (синий)
| Мопилен Резопрен (голубой)
| | Полиамидная мононить
| Полиамид / капрон моно
| Этилон (черный)
| Нейлон/монософ (черный)
| Дермалон/нейлон (черный), Новафил (голубой)
| Дафилон, сурамид (голубой, черный)
| –
| Нейлон, Резолон (белый, черный)
| | Полиамидная нить плетеная или крученая
| Полиамид/капрон крученый (белый)
| Нуролон (черный)
| Бралон/нейлон (черный)
| Серджилон плетеный (черный)
| –
| –
| –
| | Полиэфирная нить плетеная или крученая без покрытия
| Лавсан плетеный крученый (белый, зеленый)
| Мерсилен (зеленый)
| –
| –
| Марален (голубой), Дагрофил (зеленый)
| Полистер без покрытия (белый)
| Полистер без покрытия (белый, черный, зеленый)
| | Полиэфирная нить плетеная или крученая с покрытием
| Фторест (белый)
| Этибонт (зеленый)
| –
| Тигрон (синий)
| Синтофил (зеленый)
| Полистер S с покрытием (зеленый)
| Суполен с тефлоновым покрытием (зеленый)
|
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
Основная литература:
1. Кузин М.И. Хирургические болезни / М.И. Кузин, О.С. Шкроб, Н.М. Кузин. – М.: Медицина, 2005. – 784 с.
Дополнительная литература:
1. Заривчацкий М.Ф. Гнойные раны мягких тканей / М.Ф. Заривчацкий. – Пермь, 2008. – 304 с.
2. Булынин В. И. Лечение ран / В.И. Булынин, А.А. Глухов, И.П. Мошуров. – Воронеж, 1998. – 248 с.
3. Светухин А.М. Гнойная хирургия: современное состояние проблемы / А.М. Светухин, Ю.А. Амирасланов. – М.: 2004. – 640 с.
Условия постоянства, возрастания и убывания функции
Теорема 1 (условие постоянства функции). Пусть функция  определена и непрерывна на промежутке Х и имеет внутри него конечную производную определена и непрерывна на промежутке Х и имеет внутри него конечную производную 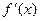 . Для того чтобы . Для того чтобы  была постоянной на Х, необходимо и достаточно условие была постоянной на Х, необходимо и достаточно условие  внутри Х. внутри Х.
Доказательство. Необходимость.
Пусть  на промежутке Х. Тогда внутри Х на промежутке Х. Тогда внутри Х 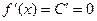 , то есть условие теоремы выполнено. , то есть условие теоремы выполнено.
Достаточность.
Зафиксируем точку  и возьмем произвольную точку и возьмем произвольную точку  . К отрезку . К отрезку  применим формулу Лагранжа (6.2) (это можно сделать, так как на этом отрезке функция применим формулу Лагранжа (6.2) (это можно сделать, так как на этом отрезке функция  непрерывна и внутри него имеет конечную производную по условию теоремы), получим непрерывна и внутри него имеет конечную производную по условию теоремы), получим  , так как , так как  внутри Х, а внутри Х, а  . Отсюда следует, что . Отсюда следует, что  , т.е. постоянна на Х. Теорема доказана. , т.е. постоянна на Х. Теорема доказана.
Теорема 2 (условие монотонности функции). Пусть функция  определена и непрерывна на промежутке Х и имеет внутри него конечную производную определена и непрерывна на промежутке Х и имеет внутри него конечную производную 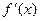 . Для того чтобы . Для того чтобы  была на Х неубывающей (невозрастающей), необходимо и достаточно условие была на Х неубывающей (невозрастающей), необходимо и достаточно условие 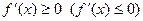 внутри Х. внутри Х.
Доказательство. Рассмотрим случай неубывающей функции.
Необходимость. Пусть функция  не убывает на Х. Возьмем внутри промежутка Х произвольную точку х и не убывает на Х. Возьмем внутри промежутка Х произвольную точку х и  . Тогда . Тогда  и, переходя в последнем неравенстве к пределу при и, переходя в последнем неравенстве к пределу при 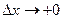 , получим , получим  . .
Достаточность. Пусть  внутри Х. Возьмем произвольные точки внутри Х. Возьмем произвольные точки 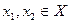 , ,  и применим формулу Лагранжа (6.2) на отрезке и применим формулу Лагранжа (6.2) на отрезке  : :  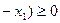 , так как , так как 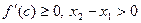 . Поэтому . Поэтому  , то есть функция , то есть функция  является неубывающей. является неубывающей.
Аналогично рассматривается случай невозрастающей функции. Теорема доказана.
Теорема 3 (достаточное условие строгой монотонности функции). Если функция  определена и непрерывна на промежутке Х, внутри него имеет конечную производную определена и непрерывна на промежутке Х, внутри него имеет конечную производную 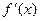 и всюду внутри Х и всюду внутри Х  , то , то  строго возрастает (убывает) на Х. строго возрастает (убывает) на Х.
Доказательство. Возьмем произвольные точки 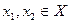 , ,  и применим к и применим к  на отрезке на отрезке  формулу Лагранжа (6.2): формулу Лагранжа (6.2):   , где , где  . Поскольку . Поскольку  , из условия , из условия  следует, что следует, что  , то есть , то есть  строго возрастает, а из условия строго возрастает, а из условия  следует, что следует, что  , то есть , то есть  строго убывает. Теорема доказана. строго убывает. Теорема доказана.
Замечание. Условие  не является необходимым для строгого возрастания (убывания) функции не является необходимым для строгого возрастания (убывания) функции  . Например, для функции . Например, для функции  в точке в точке 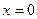 , в то же время эта функция строго возрастает на всей числовой прямой. Вообще, если , в то же время эта функция строго возрастает на всей числовой прямой. Вообще, если 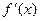 обращается в нуль в конечном числе точек, а в остальных точках сохраняет знак, то обращается в нуль в конечном числе точек, а в остальных точках сохраняет знак, то  – строго монотонная функция. Для доказательства этого достаточно применить формулу Лагранжа к промежуткам между соседними нулями производной. – строго монотонная функция. Для доказательства этого достаточно применить формулу Лагранжа к промежуткам между соседними нулями производной.
Определение 1. Функция  называется возрастающей (убывающей) в точке называется возрастающей (убывающей) в точке  , если существует окрестность , если существует окрестность 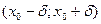 точки точки  такая, что функция определена в этой окрестности и знак приращения функции такая, что функция определена в этой окрестности и знак приращения функции 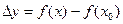 в этой окрестности совпадает со знаком (противоположен знаку) приращения аргумента. в этой окрестности совпадает со знаком (противоположен знаку) приращения аргумента.
| | | | | | | 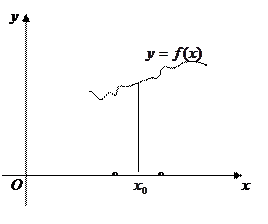 | | | | Если  , то
для , то
для  ,
для ,
для  ,
поэтому функция ,
поэтому функция  возрастает
в точке возрастает
в точке  . .
| | | |
Теорема 4 (достаточное условие монотонности функции в точке). Если функция  определена в некоторой окрестности точки определена в некоторой окрестности точки  и имеет в этой точке положительную производную и имеет в этой точке положительную производную 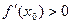 , то функция , то функция  возрастает в точке возрастает в точке  . Если же . Если же  , то , то  убывает в точке убывает в точке  . .
Доказательство. В силу теоремы 1 § 2
 , где , где  при при  . Поскольку . Поскольку  при при  , а , а 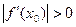 , существует , существует 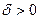 такое, что такое, что  при при 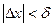 или или  . Если . Если 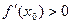 , то в окрестности , то в окрестности 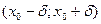  , откуда , откуда  и знак и знак  совпадает со знаком совпадает со знаком  , т.е. функция , т.е. функция  возрастает в точке возрастает в точке  . Если . Если  , то , то  , откуда , откуда 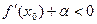 и знак и знак  противоположен знаку противоположен знаку  , т.е. функция , т.е. функция  убывает в точке убывает в точке  . Теорема доказана. . Теорема доказана.
Пример. Найдем интервалы монотонности функции  . .
Решение. Найдем область определения функции: функция существует, когда 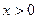 и и  , то есть , то есть  . Далее, . Далее,  = =  , в области определения , в области определения  существует. Отметим на числовой прямой область определения функции и точку существует. Отметим на числовой прямой область определения функции и точку  , в которой производная равна нулю. После этого определим в каждом из полученных промежутков знак производной с помощью пробных точек: , в которой производная равна нулю. После этого определим в каждом из полученных промежутков знак производной с помощью пробных точек:  , ,  . .
– – + 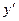
 
0 1 е
Видим, что функция убывает на интервалах (0; 1) и (1; е), возрастает на интервале  . .
Дата добавления: 2015-01-18 | Просмотры: 1688 | Нарушение авторских прав
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|

 определена и непрерывна на промежутке Х и имеет внутри него конечную производную
определена и непрерывна на промежутке Х и имеет внутри него конечную производную 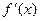 . Для того чтобы
. Для того чтобы  внутри Х.
внутри Х. на промежутке Х. Тогда внутри Х
на промежутке Х. Тогда внутри Х 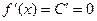 , то есть условие теоремы выполнено.
, то есть условие теоремы выполнено. и возьмем произвольную точку
и возьмем произвольную точку  . К отрезку
. К отрезку  применим формулу Лагранжа (6.2) (это можно сделать, так как на этом отрезке функция
применим формулу Лагранжа (6.2) (это можно сделать, так как на этом отрезке функция  , так как
, так как  . Отсюда следует, что
. Отсюда следует, что  , т.е. постоянна на Х. Теорема доказана.
, т.е. постоянна на Х. Теорема доказана.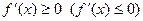 внутри Х.
внутри Х. . Тогда
. Тогда  и, переходя в последнем неравенстве к пределу при
и, переходя в последнем неравенстве к пределу при 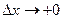 , получим
, получим  .
.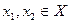 ,
,  и применим формулу Лагранжа (6.2) на отрезке
и применим формулу Лагранжа (6.2) на отрезке  :
: 
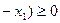 , так как
, так как 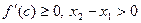 . Поэтому
. Поэтому  , то есть функция
, то есть функция  , то
, то  , где
, где  . Поскольку
. Поскольку  , из условия
, из условия  следует, что
следует, что  , то есть
, то есть  следует, что
следует, что  , то есть
, то есть  в точке
в точке 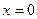 , в то же время эта функция строго возрастает на всей числовой прямой. Вообще, если
, в то же время эта функция строго возрастает на всей числовой прямой. Вообще, если  , если существует окрестность
, если существует окрестность 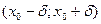 точки
точки 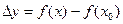 в этой окрестности совпадает со знаком (противоположен знаку) приращения аргумента.
в этой окрестности совпадает со знаком (противоположен знаку) приращения аргумента.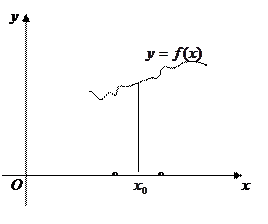
 , то
для
, то
для  ,
для
,
для  ,
поэтому функция
,
поэтому функция 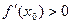 , то функция
, то функция  , то
, то  , где
, где  при
при  . Поскольку
. Поскольку 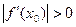 , существует
, существует 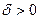 такое, что
такое, что  при
при 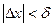 или
или  . Если
. Если  , откуда
, откуда  и знак
и знак  совпадает со знаком
совпадает со знаком  , т.е. функция
, т.е. функция  , откуда
, откуда 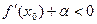 и знак
и знак  .
.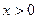 и
и  , то есть
, то есть  . Далее,
. Далее,  =
=  , в области определения
, в области определения  существует. Отметим на числовой прямой область определения функции и точку
существует. Отметим на числовой прямой область определения функции и точку  , в которой производная равна нулю. После этого определим в каждом из полученных промежутков знак производной с помощью пробных точек:
, в которой производная равна нулю. После этого определим в каждом из полученных промежутков знак производной с помощью пробных точек:  ,
,  .
.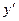


 .
.