Тригонометрические функции
При определении синуса и косинуса произвольного угла в 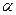 радиан пользуются окружностью, причем наиболее наглядно свойства их видны, если окружность имеет единичный радиус. радиан пользуются окружностью, причем наиболее наглядно свойства их видны, если окружность имеет единичный радиус.
 у Определение 1. Ордината точки у Определение 1. Ордината точки 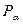 , полученной при , полученной при
повороте точки 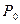 (1; 0) вокруг начала координат на (1; 0) вокруг начала координат на
угол 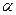 радиан, называется синусом числа радиан, называется синусом числа 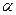 sin 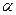
| |  , а , а
   s s 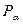 абсцисса этой точки – косинусом абсцисса этой точки – косинусом 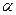 . Обозначаются . Обозначаются
соответственно sin 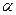 и cos и cos 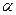 . .
О cos 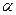 1 x 1 x
| | 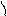  Сопоставляя каждому числу х его синус и косинус, Сопоставляя каждому числу х его синус и косинус,
J получим две функции sin х и cos х, определенные на
всей числовой прямой.
Непосредственно из определения следует, что
областью значений этих функций является отрезок 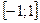 ; обе функции – периодические с основным ; обе функции – периодические с основным
периодом 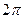 ; cos х – функция четная (так как ; cos х – функция четная (так как
cos (– 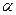 ) = cos ) = cos 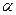 ), sin х – функция нечетная (так как sin (– ), sin х – функция нечетная (так как sin (– 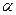 ) = – sin ) = – sin 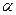 ), поэтому их графики симметричны относительно оси Оу и начала координат соответственно. ), поэтому их графики симметричны относительно оси Оу и начала координат соответственно.
sin х > 0 в I и II четвертях, sin х < 0 в III и IV четвертях, sin х = 0 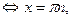 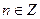 , то есть , то есть 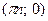 – точки пересечения графика sin х с осью Ох, (0; 0) – с осью Оу. – точки пересечения графика sin х с осью Ох, (0; 0) – с осью Оу.
cos х > 0 в I и IV четвертях, cos х < 0 во II и III четвертях, cos х = 0 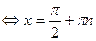 , ,
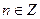 , т.е. , т.е. 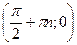 – точка пересечения графика cos х с осью Ох, (0; 1) – с осью Оу. – точка пересечения графика cos х с осью Ох, (0; 1) – с осью Оу.
Функция 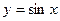 возрастает от – 1 до 1 на отрезках возрастает от – 1 до 1 на отрезках 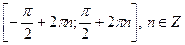 , убывает от 1 до – 1 на отрезках , убывает от 1 до – 1 на отрезках 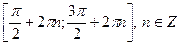 , поэтому , поэтому 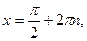 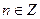 –точки максимума, –точки максимума, 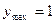 , , 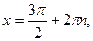 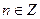 – точки минимума, – точки минимума, 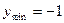 . .
Функция 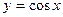 возрастает от – 1 до 1 на отрезках возрастает от – 1 до 1 на отрезках 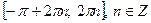 , убывает от 1 до – 1 на отрезках , убывает от 1 до – 1 на отрезках 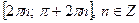 , поэтому , поэтому 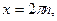 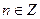 – точки максимума, – точки максимума, 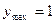 , , 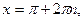 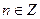 – точки минимума, – точки минимума, 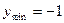 . .
Установим непрерывность функций cos х и sin х в каждой точке 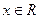 , пользуясь известным неравенством , пользуясь известным неравенством
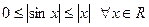 . .
Теорема 1. Функции cos х и sin х непрерывны в каждой точке числовой прямой.
Доказательство. Пусть  – произвольная точка числовой прямой. Докажем, что функция cos х непрерывна в этой точке. Имеем – произвольная точка числовой прямой. Докажем, что функция cos х непрерывна в этой точке. Имеем
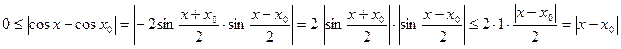
Поскольку 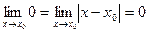 , по теореме о промежуточной переменной , по теореме о промежуточной переменной 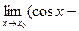 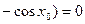 и и 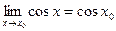 , то есть функция cos х непрерывна в точке , то есть функция cos х непрерывна в точке  и в силу произвольности точки и в силу произвольности точки 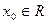 функция cos х непрерывна в каждой точке числовой прямой. функция cos х непрерывна в каждой точке числовой прямой.
По формуле приведения 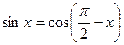 , поэтому по теореме о непрерывности сложной функции функция sin х непрерывна в каждой точке числовой прямой, так как функции cos t и , поэтому по теореме о непрерывности сложной функции функция sin х непрерывна в каждой точке числовой прямой, так как функции cos t и 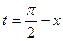 непрерывны всюду. Теорема доказана. непрерывны всюду. Теорема доказана.
Из теоремы 1 и того, что 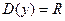 , следует, что вертикальных асимптот нет (это следует и из ограниченности функций). Поскольку , следует, что вертикальных асимптот нет (это следует и из ограниченности функций). Поскольку 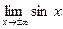 и и 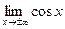 не существуют, нет и горизонтальных асимптот. Наклонных асимптот тоже нет, так как не существуют, нет и горизонтальных асимптот. Наклонных асимптот тоже нет, так как 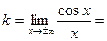 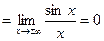 . .
Рассмотрим функцию 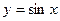 . Имеем . Имеем 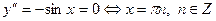 . .
 – + – + – – + – + – 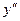 · · · · · · – 2π – π 0 π 2π 3π · · · · · · – 2π – π 0 π 2π 3π
Видим, что (π n; 0) – точки перегиба, 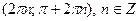 – интервалы выпуклости вверх, – интервалы выпуклости вверх, 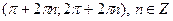 – интервалы выпуклости вниз. – интервалы выпуклости вниз.
Графиком функции 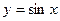 является синусоида. является синусоида.
 у у
   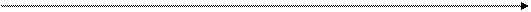
–2 π – π О π 2 π х
Из равенства 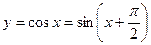 видим, что графиком функции видим, что графиком функции 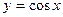 является сдвинутая влево на является сдвинутая влево на 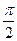 синусоида. синусоида.
 у у
   х х
– 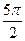 – – 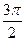 – – 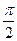 О О 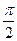 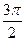 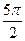
Определение 2. Тангенсом числа 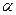 называется отношение синуса этого числа к его косинусу: называется отношение синуса этого числа к его косинусу: 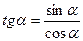 . .
Котангенсом числа 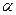 называется отношение косинуса этого числа к его синусу: называется отношение косинуса этого числа к его синусу: 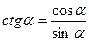 . .
Свойства функций 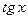 и и 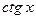 вытекают из свойств функций вытекают из свойств функций 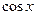 и и 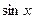 . .
Рассмотрим функцию 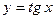 . .
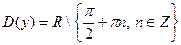 . Нечетная. Периодическая с основным периодом . Нечетная. Периодическая с основным периодом 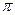 . Это следует из равенств . Это следует из равенств 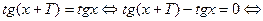 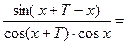 0 0 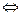 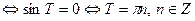 . Аналогично, . Аналогично, 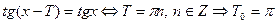 . .
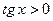 в I и III четвертях, в I и III четвертях, 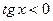 во II и IV четвертях. во II и IV четвертях.
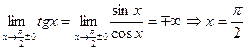 – вертикальная асимптота, в силу периодичности, – вертикальная асимптота, в силу периодичности, 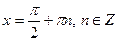 – вертикальные асимптоты. В силу периодичности – вертикальные асимптоты. В силу периодичности 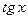 , горизонтальных и наклонных асимптот нет. Непрерывность в , горизонтальных и наклонных асимптот нет. Непрерывность в 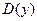 следует из теоремы о непрерывности частного непрерывных функций. следует из теоремы о непрерывности частного непрерывных функций.
(π n; 0) – точки пересечения с осью Ох, (0; 0) – точка пересечения с осью Оу.
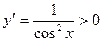 в в 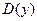 , поэтому функция , поэтому функция 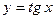 возрастает в интервалах возрастает в интервалах 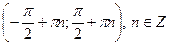 , точек экстремума нет. , точек экстремума нет.
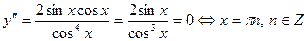 . .
 – + – + – + – + 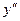 ◦ • ◦ • ◦ ◦ • ◦ • ◦ 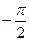 0 0 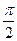 π π 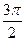
(π n; 0) – точки перегиба, 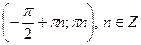 – интервалы выпуклости вверх, – интервалы выпуклости вверх, 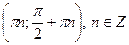 – интервалы выпуклости вниз. – интервалы выпуклости вниз.
Аналогично исследуется функция 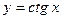 . .
     у у у у
 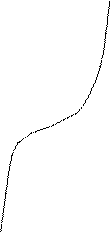   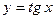 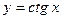
х х
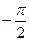 О О  О О  π π
Обратные тригонометрические функции arcsin x, arccos x, arctg x, arcctg x были рассмотрены в главе I. Их свойства устанавливаются с помощью свойств функций sin x, co s x, tg x, ctg x и теоремы о существовании и непрерывности обратной функции.
Дата добавления: 2015-01-18 | Просмотры: 708 | Нарушение авторских прав
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|

 , а
, а
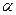 и cos
и cos 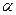 .
.
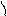
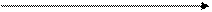 Сопоставляя каждому числу х его синус и косинус,
Сопоставляя каждому числу х его синус и косинус,
 у Определение 1. Ордината точки
у Определение 1. Ордината точки 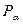 , полученной при
, полученной при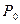 (1; 0) вокруг начала координат на
(1; 0) вокруг начала координат на

 s
s 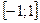 ; обе функции – периодические с основным
; обе функции – периодические с основным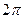 ; cos х – функция четная (так как
; cos х – функция четная (так как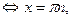
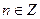 , то есть
, то есть 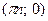 – точки пересечения графика sin х с осью Ох, (0; 0) – с осью Оу.
– точки пересечения графика sin х с осью Ох, (0; 0) – с осью Оу.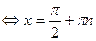 ,
,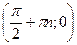 – точка пересечения графика cos х с осью Ох, (0; 1) – с осью Оу.
– точка пересечения графика cos х с осью Ох, (0; 1) – с осью Оу.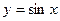 возрастает от – 1 до 1 на отрезках
возрастает от – 1 до 1 на отрезках 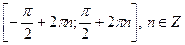 , убывает от 1 до – 1 на отрезках
, убывает от 1 до – 1 на отрезках 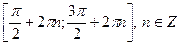 , поэтому
, поэтому 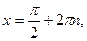
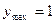 ,
, 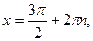
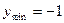 .
.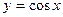 возрастает от – 1 до 1 на отрезках
возрастает от – 1 до 1 на отрезках 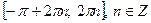 , убывает от 1 до – 1 на отрезках
, убывает от 1 до – 1 на отрезках 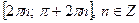 , поэтому
, поэтому 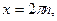
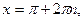
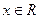 , пользуясь известным неравенством
, пользуясь известным неравенством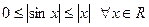 .
. – произвольная точка числовой прямой. Докажем, что функция cos х непрерывна в этой точке. Имеем
– произвольная точка числовой прямой. Докажем, что функция cos х непрерывна в этой точке. Имеем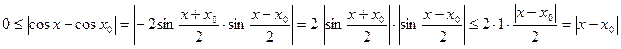
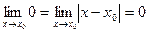 , по теореме о промежуточной переменной
, по теореме о промежуточной переменной 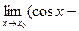
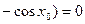 и
и 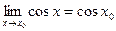 , то есть функция cos х непрерывна в точке
, то есть функция cos х непрерывна в точке 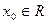 функция cos х непрерывна в каждой точке числовой прямой.
функция cos х непрерывна в каждой точке числовой прямой.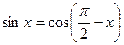 , поэтому по теореме о непрерывности сложной функции функция sin х непрерывна в каждой точке числовой прямой, так как функции cos t и
, поэтому по теореме о непрерывности сложной функции функция sin х непрерывна в каждой точке числовой прямой, так как функции cos t и 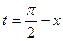 непрерывны всюду. Теорема доказана.
непрерывны всюду. Теорема доказана.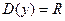 , следует, что вертикальных асимптот нет (это следует и из ограниченности функций). Поскольку
, следует, что вертикальных асимптот нет (это следует и из ограниченности функций). Поскольку 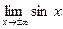 и
и 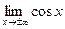 не существуют, нет и горизонтальных асимптот. Наклонных асимптот тоже нет, так как
не существуют, нет и горизонтальных асимптот. Наклонных асимптот тоже нет, так как 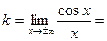
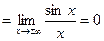 .
.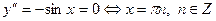 .
. – + – + –
– + – + – 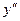 · · · · · · – 2π – π 0 π 2π 3π
· · · · · · – 2π – π 0 π 2π 3π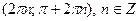 – интервалы выпуклости вверх,
– интервалы выпуклости вверх, 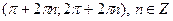 – интервалы выпуклости вниз.
– интервалы выпуклости вниз. у
у





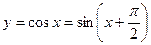 видим, что графиком функции
видим, что графиком функции 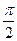 синусоида.
синусоида.




 х
х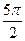 –
– 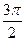 –
– 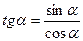 .
.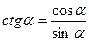 .
.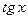 и
и 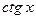 вытекают из свойств функций
вытекают из свойств функций 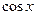 и
и 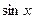 .
.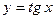 .
.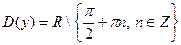 . Нечетная. Периодическая с основным периодом
. Нечетная. Периодическая с основным периодом 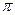 . Это следует из равенств
. Это следует из равенств 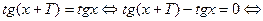
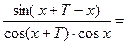 0
0 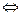
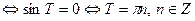 . Аналогично,
. Аналогично, 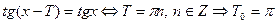 .
.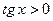 в I и III четвертях,
в I и III четвертях, 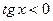 во II и IV четвертях.
во II и IV четвертях.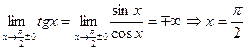 – вертикальная асимптота, в силу периодичности,
– вертикальная асимптота, в силу периодичности, 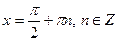 – вертикальные асимптоты. В силу периодичности
– вертикальные асимптоты. В силу периодичности 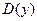 следует из теоремы о непрерывности частного непрерывных функций.
следует из теоремы о непрерывности частного непрерывных функций.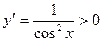 в
в 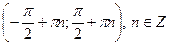 , точек экстремума нет.
, точек экстремума нет.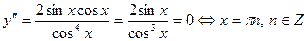 .
. – + – +
– + – + 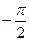 0
0 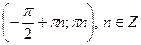 – интервалы выпуклости вверх,
– интервалы выпуклости вверх, 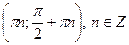 – интервалы выпуклости вниз.
– интервалы выпуклости вниз.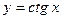 .
.




