Определение и свойства степени
Определение 1. Степенью числа а с натуральным показателем 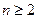 называется произведение n множителей, каждый из которых равен а: называется произведение n множителей, каждый из которых равен а:
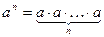 . (13.1) . (13.1)
Степенью числа а с показателем 1 называется само число а:
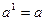 . (13.2) . (13.2)
Заметим, что в определении 1 а – любое действительное число. Равенствами (13.1) и (13.2) степень 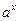 определена на множестве N натуральных чисел. определена на множестве N натуральных чисел.
Справедливы два основных свойства степени:
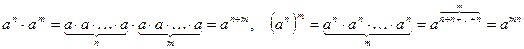 , ,
т.е. при умножении степеней с одинаковыми основаниями показатели складываются, при возведении степени в степень показатели перемножаются.
Далее степень 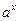 определяется на множестве всех целых чисел. определяется на множестве всех целых чисел.
Определение 2. Если 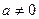 , то , то 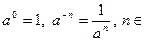 N. N.
Проверка двух основных свойств степени проводится без труда. Например,
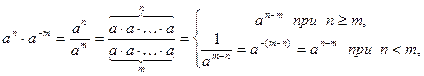
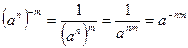 . .
Чтобы определить степень 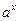 на множестве рациональных чисел, сначала определим арифметический корень n -ой степени. на множестве рациональных чисел, сначала определим арифметический корень n -ой степени.
Определение 3. Арифметическим корнем n-ой степени из неотрицательного числа а называется неотрицательное число, n -я степень которого равна а. Обозначается 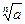 . .
Докажем, что такое число существует и единственно. Для этого рассмотрим функцию 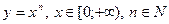 . Эта функция непрерывна и возрастает на . Эта функция непрерывна и возрастает на 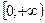 , так как , так как 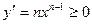 , причем , причем 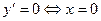 . Кроме того, . Кроме того, 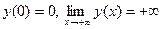 . Поэтому по теореме существования и непрерывности обратной функции на промежутке . Поэтому по теореме существования и непрерывности обратной функции на промежутке 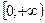 существует, возрастает и непрерывна обратная функция существует, возрастает и непрерывна обратная функция 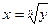 . Отсюда следует, что уравнение . Отсюда следует, что уравнение 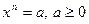 имеет единственный неотрицательный корень имеет единственный неотрицательный корень  . .
Определение 4. Если 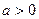 , то , то 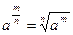 . .
Этим равенством степень 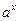 определена на множестве Q рациональных чисел. Основные свойства степени справедливы и на этом множестве. Например, справедливость равенства определена на множестве Q рациональных чисел. Основные свойства степени справедливы и на этом множестве. Например, справедливость равенства 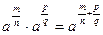 следует из того, что при взведении обеих частей этого равенства в степень nq получаем: следует из того, что при взведении обеих частей этого равенства в степень nq получаем: 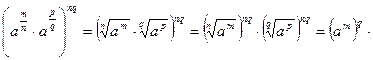 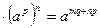 , , 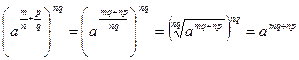 , т.е. одинаковые выражения. , т.е. одинаковые выражения.
Определим далее степень 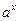 на множестве R всех действительных чисел. Для этого установим сначала несколько вспомогательных утверждений. на множестве R всех действительных чисел. Для этого установим сначала несколько вспомогательных утверждений.
Лемма 1. Для любого иррационального числа 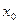 существует возрастающая последовательность рациональных чисел существует возрастающая последовательность рациональных чисел 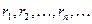 , сходящаяся к , сходящаяся к 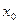 . .
Доказательство. Рассмотрим последовательность чисел 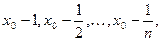 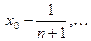 . В силу свойства усиленной плотности множества R действительных чисел между числами . В силу свойства усиленной плотности множества R действительных чисел между числами 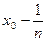 и и 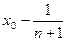 найдется рациональное число найдется рациональное число 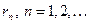 , то есть , то есть 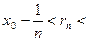 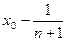 . Очевидно, что последовательность . Очевидно, что последовательность 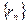 возрастающая и сходится к возрастающая и сходится к
 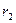 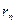
 • • • • • • • • • • • • • • • • • •
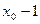 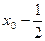 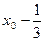 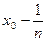 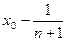 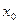
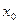 по теореме о промежуточной переменной, так как по теореме о промежуточной переменной, так как 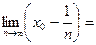 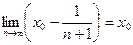 . Лемма доказана. . Лемма доказана.
Лемма 2. Если 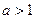 , то функция , то функция 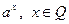 возрастает. возрастает.
Доказательство. Заметим, что если 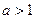 , то и , то и 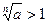 , где n – натуральное число. Это следует из возрастания функции , где n – натуральное число. Это следует из возрастания функции 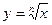 (см. доказательство существования арифметического корня). Поэтому для (см. доказательство существования арифметического корня). Поэтому для 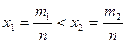 имеем имеем 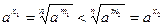 . Поскольку знаменатели рациональных чисел всегда можно сделать общими, утверждение доказано. . Поскольку знаменатели рациональных чисел всегда можно сделать общими, утверждение доказано.
Лемма 3. Если 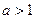 , то , то 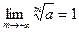 . .
Доказательство. Поскольку 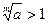 (см. доказательство леммы 2), положим (см. доказательство леммы 2), положим 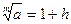 , где , где  . Тогда . Тогда 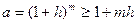 по неравенству Бернулли, или по неравенству Бернулли, или 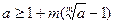 . Отсюда . Отсюда 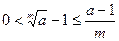 и по теореме о промежуточной переменной и по теореме о промежуточной переменной 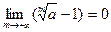 , то есть , то есть 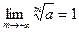 . Лемма доказана. . Лемма доказана.
Лемма 4. Для любой последовательности рациональных чисел 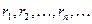 , сходящейся к нулю, последовательность , сходящейся к нулю, последовательность 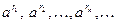 (где (где 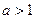 ) сходится к 1, т.е. ) сходится к 1, т.е. 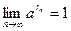 . .
Доказательство. Возьмем 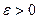 произвольно. Поскольку по лемме 3 произвольно. Поскольку по лемме 3 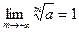 , , 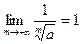 , то найдется номер , то найдется номер 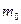 такой, что такой, что 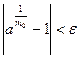 и и 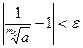 , откуда , откуда 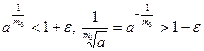 . А так как . А так как 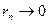 при при 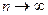 , то найдется номер , то найдется номер  , такой, что для , такой, что для 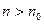 будет будет 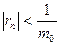 , то есть , то есть 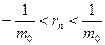 и по лемме 2 и по лемме 2 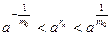 , откуда , откуда 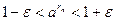 и и 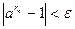 для для 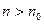 . Лемма доказана. . Лемма доказана.
Лемма 5. Пусть 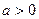 и и 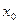 – произвольное иррациональное число. Тогда для любой последовательности рациональных чисел – произвольное иррациональное число. Тогда для любой последовательности рациональных чисел 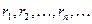 , сходящейся к , сходящейся к 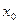 , последовательность , последовательность 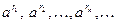 сходится к одному и тому же пределу. сходится к одному и тому же пределу.
Доказательство. Если 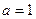 , то , то 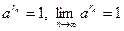 , то есть утверждение справедливо. , то есть утверждение справедливо.
Пусть 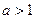 . Рассмотрим сначала какую-нибудь неубывающую последовательность рациональных чисел . Рассмотрим сначала какую-нибудь неубывающую последовательность рациональных чисел 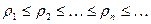 , сходящуюся к , сходящуюся к 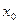 . Такая последовательность существует по лемме 1. Тогда по лемме 2 . Такая последовательность существует по лемме 1. Тогда по лемме 2
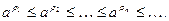 (13.3) (13.3)
Возьмем рациональное число 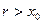 . Тогда . Тогда 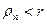 и по лемме 2 и по лемме 2 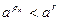 для всех n, т.е. последовательность (13.3) ограничена сверху. По теореме о существовании предела монотонной и ограниченной последовательности существует для всех n, т.е. последовательность (13.3) ограничена сверху. По теореме о существовании предела монотонной и ограниченной последовательности существует 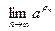 , который мы обозначим буквой А. При этом , который мы обозначим буквой А. При этом 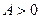 , так как , так как 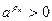 и последовательность (13.3) неубывающая. и последовательность (13.3) неубывающая.
Пусть теперь 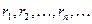 – произвольная последовательность рациональных чисел, сходящаяся к – произвольная последовательность рациональных чисел, сходящаяся к 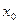 . Тогда последовательность рациональных чисел . Тогда последовательность рациональных чисел 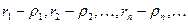 сходится к нулю и по лемме 4 сходится к нулю и по лемме 4 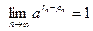 . Следовательно, . Следовательно, 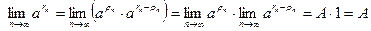 и утверждение леммы справедливо. и утверждение леммы справедливо.
Рассмотрим теперь случай 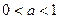 . Положим . Положим 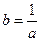 . Тогда . Тогда 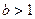 и по уже доказанному для любой последовательности рациональных чисел и по уже доказанному для любой последовательности рациональных чисел 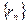 , , 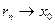 , существует один и тот же предел , существует один и тот же предел 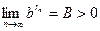 . Отсюда . Отсюда 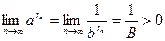 . .
Лемма доказана.
Определение 5. Пусть 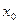 – произвольное иррациональное число, – произвольное иррациональное число, 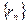 – любая последовательность рациональных чисел, сходящаяся к – любая последовательность рациональных чисел, сходящаяся к 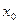 , , 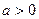 . Тогда полагают . Тогда полагают
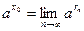 . (13.4) . (13.4)
Заметим, что формула (13.4) справедлива и в случае, когда 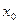 – рациональное число. Тогда – рациональное число. Тогда 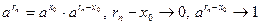 и и 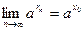 . Таким образом, формула (13.4) имеет место для любого действительного числа . Таким образом, формула (13.4) имеет место для любого действительного числа 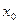 . .
Теорема 1. Справедливы равенства
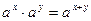 , (13.5) , (13.5)
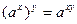 , (13.6) , (13.6)
где 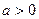 , а х, у – любые действительные числа. , а х, у – любые действительные числа.
Доказательство. Пусть 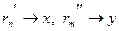 , где , где 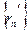 и и 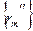 – последовательности рациональных чисел. Поскольку для рациональных х и у равенство (13.5) справедливо, имеем – последовательности рациональных чисел. Поскольку для рациональных х и у равенство (13.5) справедливо, имеем 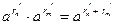 и в пределе при и в пределе при 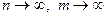 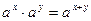 . .
Докажем теперь (13.6). Имеем 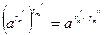 . Переходя к пределу при . Переходя к пределу при 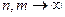 , получим , получим 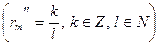 : :
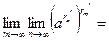 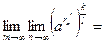 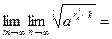 (непрерывность обратной функции, т.е. (непрерывность обратной функции, т.е. 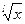 ) = ) = 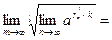 (см. (13.4)) = (см. (13.4)) = 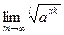 = = 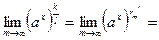 (см. (13.4)) = (см. (13.4)) = 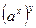 , ,
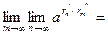 (см. (13.4)) = (см. (13.4)) = 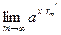 = (непрерывность показательной функции) = = (непрерывность показательной функции) = 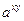 , поэтому , поэтому 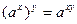 . Теорема доказана. . Теорема доказана.
Замечание. Аналогично можно доказать, что 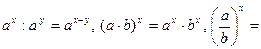 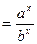 , где , где 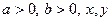 – любые действительные числа. – любые действительные числа.
Дата добавления: 2015-01-18 | Просмотры: 1561 | Нарушение авторских прав
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|

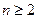 называется произведение n множителей, каждый из которых равен а:
называется произведение n множителей, каждый из которых равен а: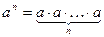 . (13.1)
. (13.1)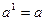 . (13.2)
. (13.2)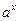 определена на множестве N натуральных чисел.
определена на множестве N натуральных чисел.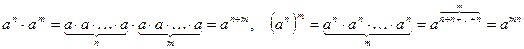 ,
,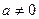 , то
, то 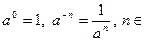 N.
N.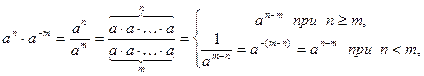
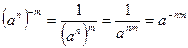 .
.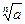 .
.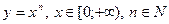 . Эта функция непрерывна и возрастает на
. Эта функция непрерывна и возрастает на 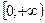 , так как
, так как 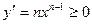 , причем
, причем 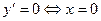 . Кроме того,
. Кроме того, 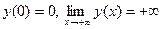 . Поэтому по теореме существования и непрерывности обратной функции на промежутке
. Поэтому по теореме существования и непрерывности обратной функции на промежутке 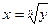 . Отсюда следует, что уравнение
. Отсюда следует, что уравнение 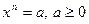 имеет единственный неотрицательный корень
имеет единственный неотрицательный корень  .
.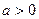 , то
, то 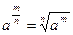 .
.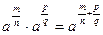 следует из того, что при взведении обеих частей этого равенства в степень nq получаем:
следует из того, что при взведении обеих частей этого равенства в степень nq получаем: 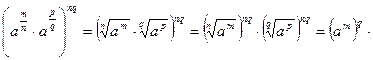
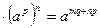 ,
, 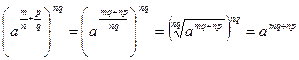 , т.е. одинаковые выражения.
, т.е. одинаковые выражения. существует возрастающая последовательность рациональных чисел
существует возрастающая последовательность рациональных чисел 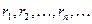 , сходящаяся к
, сходящаяся к 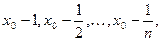
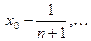 . В силу свойства усиленной плотности множества R действительных чисел между числами
. В силу свойства усиленной плотности множества R действительных чисел между числами 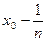 и
и 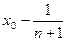 найдется рациональное число
найдется рациональное число 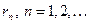 , то есть
, то есть 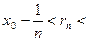
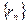 возрастающая и сходится к
возрастающая и сходится к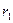
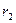
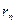
 • • • • • • • • •
• • • • • • • • •
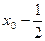
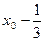
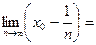
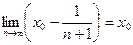 . Лемма доказана.
. Лемма доказана.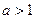 , то функция
, то функция 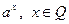 возрастает.
возрастает.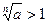 , где n – натуральное число. Это следует из возрастания функции
, где n – натуральное число. Это следует из возрастания функции 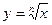 (см. доказательство существования арифметического корня). Поэтому для
(см. доказательство существования арифметического корня). Поэтому для 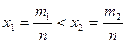 имеем
имеем 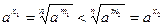 . Поскольку знаменатели рациональных чисел всегда можно сделать общими, утверждение доказано.
. Поскольку знаменатели рациональных чисел всегда можно сделать общими, утверждение доказано.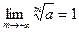 .
.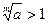 (см. доказательство леммы 2), положим
(см. доказательство леммы 2), положим 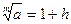 , где
, где  . Тогда
. Тогда 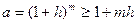 по неравенству Бернулли, или
по неравенству Бернулли, или 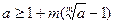 . Отсюда
. Отсюда 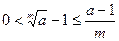 и по теореме о промежуточной переменной
и по теореме о промежуточной переменной 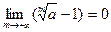 , то есть
, то есть 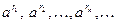 (где
(где 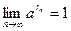 .
.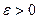 произвольно. Поскольку по лемме 3
произвольно. Поскольку по лемме 3 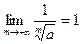 , то найдется номер
, то найдется номер 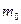 такой, что
такой, что 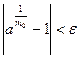 и
и 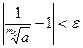 , откуда
, откуда 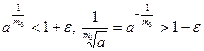 . А так как
. А так как 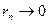 при
при 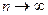 , то найдется номер
, то найдется номер  , такой, что для
, такой, что для 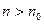 будет
будет 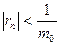 , то есть
, то есть 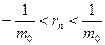 и по лемме 2
и по лемме 2 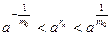 , откуда
, откуда 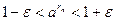 и
и 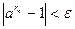 для
для 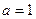 , то
, то 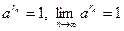 , то есть утверждение справедливо.
, то есть утверждение справедливо.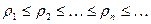 , сходящуюся к
, сходящуюся к 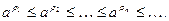 (13.3)
(13.3)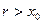 . Тогда
. Тогда 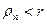 и по лемме 2
и по лемме 2 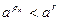 для всех n, т.е. последовательность (13.3) ограничена сверху. По теореме о существовании предела монотонной и ограниченной последовательности существует
для всех n, т.е. последовательность (13.3) ограничена сверху. По теореме о существовании предела монотонной и ограниченной последовательности существует 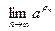 , который мы обозначим буквой А. При этом
, который мы обозначим буквой А. При этом 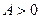 , так как
, так как 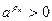 и последовательность (13.3) неубывающая.
и последовательность (13.3) неубывающая.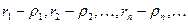 сходится к нулю и по лемме 4
сходится к нулю и по лемме 4 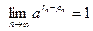 . Следовательно,
. Следовательно, 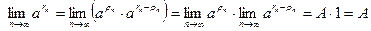 и утверждение леммы справедливо.
и утверждение леммы справедливо.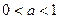 . Положим
. Положим 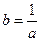 . Тогда
. Тогда 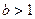 и по уже доказанному для любой последовательности рациональных чисел
и по уже доказанному для любой последовательности рациональных чисел 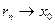 , существует один и тот же предел
, существует один и тот же предел 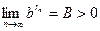 . Отсюда
. Отсюда 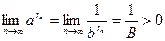 .
.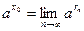 . (13.4)
. (13.4)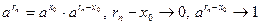 и
и 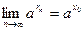 . Таким образом, формула (13.4) имеет место для любого действительного числа
. Таким образом, формула (13.4) имеет место для любого действительного числа 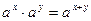 , (13.5)
, (13.5)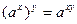 , (13.6)
, (13.6)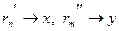 , где
, где 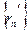 и
и 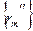 – последовательности рациональных чисел. Поскольку для рациональных х и у равенство (13.5) справедливо, имеем
– последовательности рациональных чисел. Поскольку для рациональных х и у равенство (13.5) справедливо, имеем 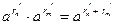 и в пределе при
и в пределе при 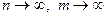
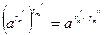 . Переходя к пределу при
. Переходя к пределу при 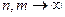 , получим
, получим 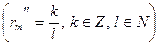 :
: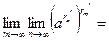
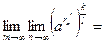
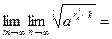 (непрерывность обратной функции, т.е.
(непрерывность обратной функции, т.е. 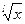 ) =
) = 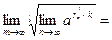 (см. (13.4)) =
(см. (13.4)) = 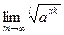 =
= 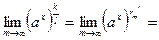 (см. (13.4)) =
(см. (13.4)) = 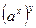 ,
,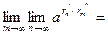 (см. (13.4)) =
(см. (13.4)) = 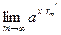 = (непрерывность показательной функции) =
= (непрерывность показательной функции) = 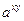 , поэтому
, поэтому 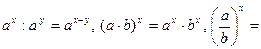
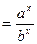 , где
, где 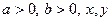 – любые действительные числа.
– любые действительные числа.